Тема: « Задачи на смеси, сплавы, растворы»Кондратьев ИванРоссия, Забайкальский край, Карымский район, село Тыргетуй МОУ СОШ с.Тыргетуй 9 класс. Научная статьяНаучные понятия: смесь, сплав, раствор, концентрация.В жизни мы встречаемся не с чистыми веществами, а со смесями, т.е. соединениями веществ.Смеси¹ могут быть жидкими, твёрдыми и газообразными. Раствор – это однородная система, состоящая из частиц растворённого вещества, растворителя и продуктов их взаимодействия.Сплавы² – это материалы с характерными свойствами, состоящие из двух или более компонентов, из которых по крайней мере один - металл.Отношение массы растворённого вещества к общей массе раствора называют массовой долей растворённого вещества. Массовую долю выражают в долях единицы или процентах.W( в долях)=m(вещество): m(раствор),W( в %)=w* 100%Массовую долю, выраженную в процентах, называют концентрацией вещества.Тема: « Задачи на смеси, сплавы, растворы»Кондратьев ИванРоссия, Забайкальский край, Карымский район, село Тыргетуй МОУ СОШ с.Тыргетуй 9 класс. Методы решения задач на сплавы, смеси, растворы.Существуют несколько способов решения задач по данной теме:1)Метод прямоугольников;2)Арифметический способ;3)Алгебраический способ;4)Табличный способ;5) Схематический способ;6) Метод «стаканчиков»Рассмотрим методы решения задач на сплавы , смеси, растворы:Решение задач на смеси методом прямоугольников.Одним из универсальных методов является метод прямоугольников. Данный способ удобен, так как зрительное восприятие данных, расположенных в определенном задуманном порядке, позволяет компактно представить процессы соединения растворов, упростить составление уравнения, а также облегчить процесс как решения, так и проверки задачи. Наиболее распространены задачи, в которых из двух смесей (растворов или сплавов) получается новая смесь (раствор или сплав). Этот способ основан на приравнивании площадей равновеликих прямоугольников. Рассмотрим типовые задачи.Задача 1³.Смешали 30%-й раствор соляной кислоты с 10%-ым раствором и получили 600 г 15%-го раствора. Сколько граммов каждого раствора надо было взять?

---

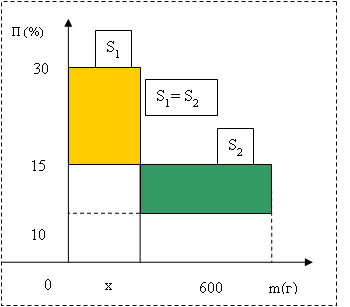
Решение:Обозначим x массу первого раствора, тогда масса второго (600 - x).15x = 5 (600- x)x =150 г.Ответ: 150 г и 450 г.Решение других задач методом прямоугольников смотрите приложение 1.Метод прямоугольников можно назвать «красивым», но составление рисунка занимает много времени. Табличный метод.Решение задач на концентрациюВ данных задачах речь идет о сплавах, растворах и смесях, которые получаются при сплавлении или смешивании различных веществ. При решении таких задач принимаются некоторые допущения. Первое: если смешиваются два раствора, масса которых х и у, то получившаяся смесь будет иметь массу х + у. Второе: получившиеся смеси и сплавы имеют однородную консистенцию.В смесях и растворах содержится некоторая масса чистого вещества, которую и отражает концентрация. При решении таких задач удобно пользоваться таблицей, которая помогает понять задачу и по которой легче составить уравнение или систему, так как  она нагляднее и короче обычной записи с пояснениями. Зрительное восприятие определенного расположения величин в таблице дает дополнительную информацию, облегчающую процесс решения задачи и её проверки.Такая таблица имеет стандартный вид, который легко использовать для записи любой задачи данного типа:

Масса твёрдого вещества (m тв)

Масса вещества (m р-ра)

Концентрация, % (К)

1-ое вещество

m1

M1

К1 = m1/ M1*100%

2-ое вещество

m2

M2

К2 = m2/ M2*100%

---

Раствор

m = m1  +  m2

M = M1  + M2

К = m / M*100%

Алгоритм решения задачи на сплавы, растворы и смеси:Изучить условия задачи. Выбрать неизвестные величины (их обозначают буквами х, у и т.д.), относительно которых составить пропорции, этим, мы создаем математическую модель ситуации, описанной в условии задачи.Используя условия задачи, определить все взаимосвязи между данными величинами.Составить математическую модель задачи и решить ее.Изучить полученное решение, провести критический анализ результата.Задача 1.Имеются два раствора соли массой 80 г и 120 г. В первом растворе содержится 12 г соли, а во втором – 15 г соли. Какова концентрация этих растворов. Какой будет концентрация, если оба эти раствора смешать?Решение:

m тв

m р-ра

K

1 раствор

12 г

80 г

?

2 раствор

15 г

120 г

?

Смесь

27 г

200 г

?

К = 12/80*100% = 3/20*100% = 15 (%) – концентрация 1 раствора.К = 15/120*100% = 5/40*100% = 12,5 (%) – концентрация 2 раствора.К = 27/200*100% = 27/2 = 13,5 (%) – концентрация смеси.Ответ: 15; 12,5; 13,5.Табличный способ позволяет видеть условие задачи,для этого надо запомнить название столбцов и заполнить таблицу.Старинный способ решения⁴Таким способом можно решать задачи на смешивание (сплавление) любого числа веществ. Задачам подобного типа уделялось значительное внимание в старинных рукописях и «Арифметике» Леонтия Филипповича Магницкого (1703г).  (Лео́нтийФили́пповичМагни́цкий⁵ (при рождении Телятин; 9 (19) июня 1669, Осташков — 19 (30) октября 1739, Москва) — русский математик, педагог. Преподаватель математики в Школе математических и навигацких наук в Москве (с 1701 по 1739), автор первой в России учебной энциклопедии по математике).

---

 

Данный способ позволяет получить правильный ответ за очень короткое время и с минимальными усилиями.

Решим предыдущую задачу 1 старинным способом.

Друг под другом пишутся процентные содержания меди в имеющихся сплавах, слева от них и примерно посередине – процентное содержание меди в сплаве, который должен получиться после сплавления. Соединив написанные числа черточками, получим такую схему:

Рассмотрим пары 75 и 72; 75 и 80. В каждой паре из большего числа вычтем меньшее, и результат запишем в конце соответствующей стрелочки. Получится такая схема:

                  72                5 

75 

                 80                 3       

Из нее делается заключение, что 72%-ного сплава следует взять 5 частей, а 80%-ного – 3 части (800:(5 + 3) = 100 г приходится на одну часть.) Таким образом, для получения 800 г 75%-ного сплава нужно взять 72%-ного сплава 100·5 = 500 г, а 80%-ного – 100·3 = 300 г.

Ответ:500г, 300г.

Решение других задач методом Магницкого смотрите приложение 2.

Правило креста или квадрат Пирсона

(Карл (Чарлз) Пирсон (27 марта 1857, Лондон — 27 апреля 1936, там же) — выдающийся английский математик, статистик, биолог и философ; основатель математической статистики, автор свыше 650 опубликованных научных работ).

Очень часто при решении задач приходится встречаться со случаями приготовления растворов с определенной массовой долей растворенного вещества, смешением двух растворов разной концентрации или разбавлением крепкого раствора водой. В некоторых случаях можно провести достаточно сложный арифметический расчёт. Однако это малопродуктивно. Чаще для этого лучше применить правило смешения (диагональную модель «квадрата Пирсона», или, что тоже самое, правило креста).

Допустим, нужно приготовить раствор определенной концентрации, имея в распоряжении два раствора с более высокой и менее высокой концентрацией, чем нужно нам. Тогда, если обозначить массу первого раствора через m₁, а второго – через m₂, то при смешивании общая масса смеси будет складываться из суммы этих масс. Пусть массовая доля растворённого вещества в первом растворе – ₁, во втором – ₂, а в их смеси – ₃. Тогда общая масса растворённого вещества в смеси будет складываться из масс растворённого вещества в исходных растворах:

---

m₁∙₁ + m₂∙₂ = ₃(m₁ + m₂). Отсюда m₁(₁ – ₃) = m₂(₃ – ₂), .Видно, что отношение массы первого раствора к массе второго раствора есть отношение разности массовых долей растворённого вещества в смеси и во втором растворе к разности соответствующих величин в первом растворе и в смеси.При решении задач на растворы с разными концентрациями чаще всего применяют диагональную схему правила смешения. При расчётах записывают одну над другой массовые доли растворённого вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение. Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.ω₁                       ω₃ – ω₂                ω₃                              ω₂                       ω₁ – ω₃    ω₁, ω₂ – массовые части первого и второго растворов соответственно.Для пояснения этого правила сначала решим простейшую задачу.Задача. Морская вода содержит 5% соли (по массе). Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составила 1,5%?5%                          1,5%          30 кг                                      1,5%                                                0%                         3,5%          х кг                        Ответ: 7 килограммов.Данный метод может использоваться и при решения задач на смеси и сплавы. Отлили часть раствора, отрезали кусок сплава. При этой операции остается неизменной концентрация веществ.Алгебраический способ⁶Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты.Итак, пусть смесь массы М содержит некоторое вещество массой m. Тогда:-  концентрацией данного вещества в смеси (сплаве) называется величина c = m/M;-  процентным содержанием данного вещества называется величина 

---

Смотрите также файлы

• Млекопитающие.docx

• Реферат ученика 11б класса Полякова Виктора.docx

• Технология моделирования транспортной инфраструктуры.docx

• Реферат по дисциплине Философские проблемы науки и техники на тему Эпоха Возрождения как подготовительный этап к обоснованию новой науки. Гуманизм и самореализация творческой личности.pdf

• Отметить вопрос Текст вопроса Возвращены авансы покупателям и заказчикам отражается записью.docx