ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.11.2023
Просмотров: 37
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
с× 100%;
Из последней формулы следует, что при известных величинах концентрации вещества и общей массы смеси (сплава) масса данного вещества определяется по формуле m=c×M.
Задачи на смеси (сплавы) можно разделить на два вида:
1. Задаются, например, две смеси (сплава) с массами m1 и m2 и с концентрациями в них некоторого вещества, равными соответственно с1 и с2. Смеси (сплавы) сливают (сплавляют). Требуется определить массу этого вещества в новой смеси (сплаве) и его новую концентрацию. Ясно, что в новой смеси (сплаве) масса данного вещества равна c1m1+c2m2 или c(m1+m2), тогда получаем уравнение: c1m1+c2m2 = c(m1+m2).
2. Задается некоторый объем смеси (сплава) и от этого объема начинают отливать (убирать) определенное количество смеси (сплава), а затем доливать (добавлять) такое же или другое количество смеси (сплава) с такой же концентрацией данного вещества или с другой концентрацией. Эта операция проводится несколько раз.
При решении таких задач необходимо установить контроль за количеством данного вещества и его концентрацией при каждом отливе, а также при каждом доливе смеси. В результате такого контроля получаем разрешающее уравнение. Рассмотрим конкретные задачи.
Задача №1.
Из сосуда ёмкостью 54 литра, наполненного кислотой, вылили несколько литров и доли сосуд водой. Потом опять вылили столько же литров смеси. Тогда в оставшейся в сосуде смеси оказалось 24 литра чистой кислоты. Сколько кислоты вылили в первый раз?
Решение.
Пусть x литров кислоты вылили в первый раз. Тогда в сосуде осталось (54-x) литров. Долив сосуд водой, получим 54 литра смеси, в которой растворилось (54 - х) литров кислоты. Значит, в одном литре смеси содержится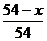
литров кислоты. Всего за два раза вылили= 30 литров кислоты. В результате получили уравнение: x + x× 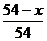= 30.
Решив это уравнение, найдём два корня: х=90 и х=18. Ясно, что значение 90 не удовлетворяет условию задачи.
Ответ: в первый раз было вылито 18 литров кислоты.
Решение других задач алгебраическим методом смотрите приложение 3.
При решении задач на смеси считается, что рассматриваемые смеси однородны: не делается различия между литром как единицей массы и как единицей ёмкости).
Этот способ универсальный и им можно пользоваться
Метод стаканчиков7
Данный метод заключается в следующем: берут два стакана с раствором, сливают их в третий стакан. Условие задачи – краткая запись в виде трёх стаканов. Проценты заменяем дробью от числа. В каждом стакане: раствор
вещество
Учитывая, что объём вещества в третьем стакане равен сумме объёмов вешеств в первом и втором стаканах, составляют уравнение , либо систему уравнений.
Решение других задач методом стаканчиков смотрите приложение 4.
Метод стаканчиков можно использовать при решении самых сложных задач ЕГЭ.
1 Габриелян О. С.Химия 8 класс.-учебник.М:2010
2 Габриелян О.С. Химия 9 класс.- учебник .М: 2010
3 Материалы курса «Текстовые задачи в школьном курсе математики» лекция 1 – 4
4 Захаров А. Е. Учимся решать задачи на смеси и сплавы// Математика для школьников. 2006. № 3 с. 18 – 21
5 Советский энциклопедический словарь . Москва. Изд. «Советская энциклопедия». 1982. С.740
6 Задачи на смеси и сплавы. Журнал «Математика в школе». № 6. 2004г.
7 Методический журнал для учителей математики «Математика». Изд. Первое сентября. № 11, 2012. С. 33 – 35
Из последней формулы следует, что при известных величинах концентрации вещества и общей массы смеси (сплава) масса данного вещества определяется по формуле m=c×M.
Задачи на смеси (сплавы) можно разделить на два вида:
1. Задаются, например, две смеси (сплава) с массами m1 и m2 и с концентрациями в них некоторого вещества, равными соответственно с1 и с2. Смеси (сплавы) сливают (сплавляют). Требуется определить массу этого вещества в новой смеси (сплаве) и его новую концентрацию. Ясно, что в новой смеси (сплаве) масса данного вещества равна c1m1+c2m2 или c(m1+m2), тогда получаем уравнение: c1m1+c2m2 = c(m1+m2).
2. Задается некоторый объем смеси (сплава) и от этого объема начинают отливать (убирать) определенное количество смеси (сплава), а затем доливать (добавлять) такое же или другое количество смеси (сплава) с такой же концентрацией данного вещества или с другой концентрацией. Эта операция проводится несколько раз.
При решении таких задач необходимо установить контроль за количеством данного вещества и его концентрацией при каждом отливе, а также при каждом доливе смеси. В результате такого контроля получаем разрешающее уравнение. Рассмотрим конкретные задачи.
Задача №1.
Из сосуда ёмкостью 54 литра, наполненного кислотой, вылили несколько литров и доли сосуд водой. Потом опять вылили столько же литров смеси. Тогда в оставшейся в сосуде смеси оказалось 24 литра чистой кислоты. Сколько кислоты вылили в первый раз?
Решение.
Пусть x литров кислоты вылили в первый раз. Тогда в сосуде осталось (54-x) литров. Долив сосуд водой, получим 54 литра смеси, в которой растворилось (54 - х) литров кислоты. Значит, в одном литре смеси содержится
литров кислоты. Всего за два раза вылили= 30 литров кислоты. В результате получили уравнение: x + x× = 30.Решив это уравнение, найдём два корня: х=90 и х=18. Ясно, что значение 90 не удовлетворяет условию задачи.
Ответ: в первый раз было вылито 18 литров кислоты.
Решение других задач алгебраическим методом смотрите приложение 3.
При решении задач на смеси считается, что рассматриваемые смеси однородны: не делается различия между литром как единицей массы и как единицей ёмкости).
Этот способ универсальный и им можно пользоваться
Метод стаканчиков7
Данный метод заключается в следующем: берут два стакана с раствором, сливают их в третий стакан. Условие задачи – краткая запись в виде трёх стаканов. Проценты заменяем дробью от числа. В каждом стакане: раствор
вещество
Учитывая, что объём вещества в третьем стакане равен сумме объёмов вешеств в первом и втором стаканах, составляют уравнение , либо систему уравнений.
Решение других задач методом стаканчиков смотрите приложение 4.
Метод стаканчиков можно использовать при решении самых сложных задач ЕГЭ.
1 Габриелян О. С.Химия 8 класс.-учебник.М:2010
2 Габриелян О.С. Химия 9 класс.- учебник .М: 2010
3 Материалы курса «Текстовые задачи в школьном курсе математики» лекция 1 – 4
4 Захаров А. Е. Учимся решать задачи на смеси и сплавы// Математика для школьников. 2006. № 3 с. 18 – 21
5 Советский энциклопедический словарь . Москва. Изд. «Советская энциклопедия». 1982. С.740
6 Задачи на смеси и сплавы. Журнал «Математика в школе». № 6. 2004г.
7 Методический журнал для учителей математики «Математика». Изд. Первое сентября. № 11, 2012. С. 33 – 35