Федеральное агентство по образованию

Дальневосточный государственный технический университет

(ДВПИ им. В.В. Куйбышева)


Соотношение теплоемкостей воздуха

при постоянном давлении и постоянном объеме
Методические указания

к лабораторной работе №16

по курсу физики для студентов дневной и заочной форм

обучения всех технических специальностей

Владивосток ∙2009

Одобрено научно – методическим советом университета
УДК 53.082.1; 531.76

И88
Соотношение теплоемкостей воздуха при постоянном давлении и постоянном объеме: метод. указания / сост. В.В. Зауткин. – Владивосток: Изд-во ДВГТУ, 2009. – 8с.

В методических указаниях приводятся краткие сведения по термодинамике изопроцессов в идеальных газах, получена теоретическая формула для соотношения теплоемкостей газа при постоянном давлении и постоянном объеме. Дано описание установки для экспериментальной проверки указанных теплоемкостей (методом Клемана – Дезорма), приведены необходимые рекомендации по проведению опытов, обработке их результатов, а так же вопросы для самоконтроля.

Методические указания предназначены для студентов дневной и заочной форм обучения всех технических специальностей университета.


Печатается с оригинал-макета, подготовленного автором





Типография ДВГТУ, 690950, Владивосток, Пушкинская, 10

Лабораторная работа №16

Соотношение теплоёмкостей воздуха

при постоянном давлении и постоянном объёме

Цель работы: определить отношение удельных теплоемкостей воздуха 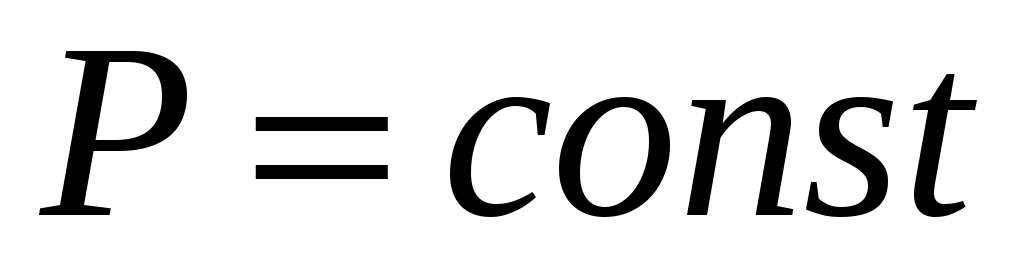при и при 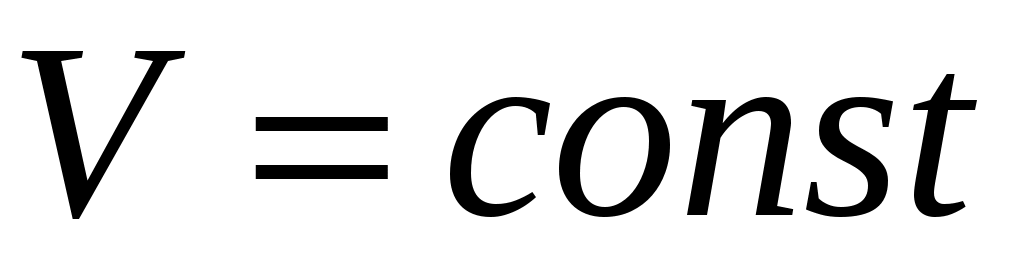методом Клемана-Дезорма.

Постановка задачи

Теплоёмкость– одно из важнейших понятий в термодинамике. Теплоём­костью тела (газообразного, жидкого, твёрдого) называют отношение количества тепла Q, сообщенного телу при нагревании, к изменению его температуры :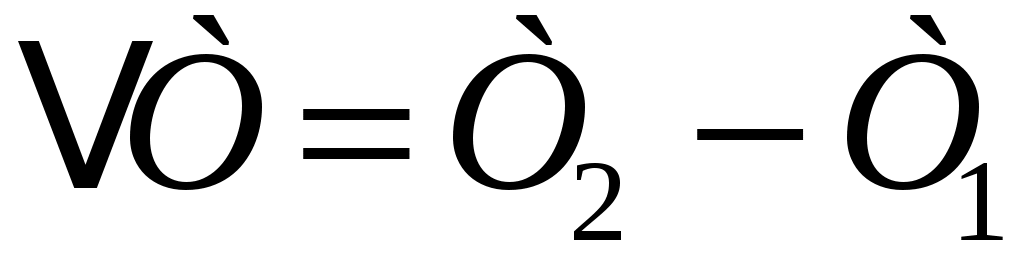

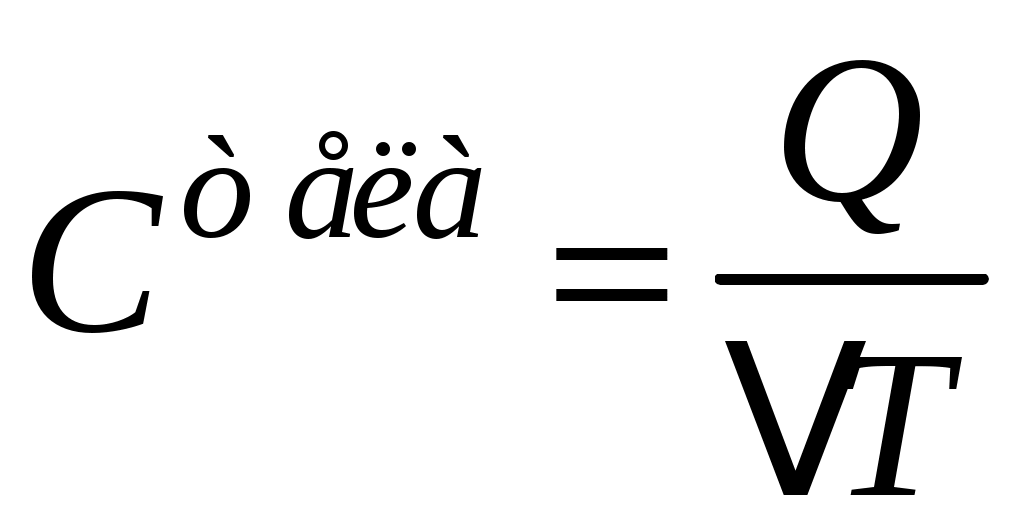
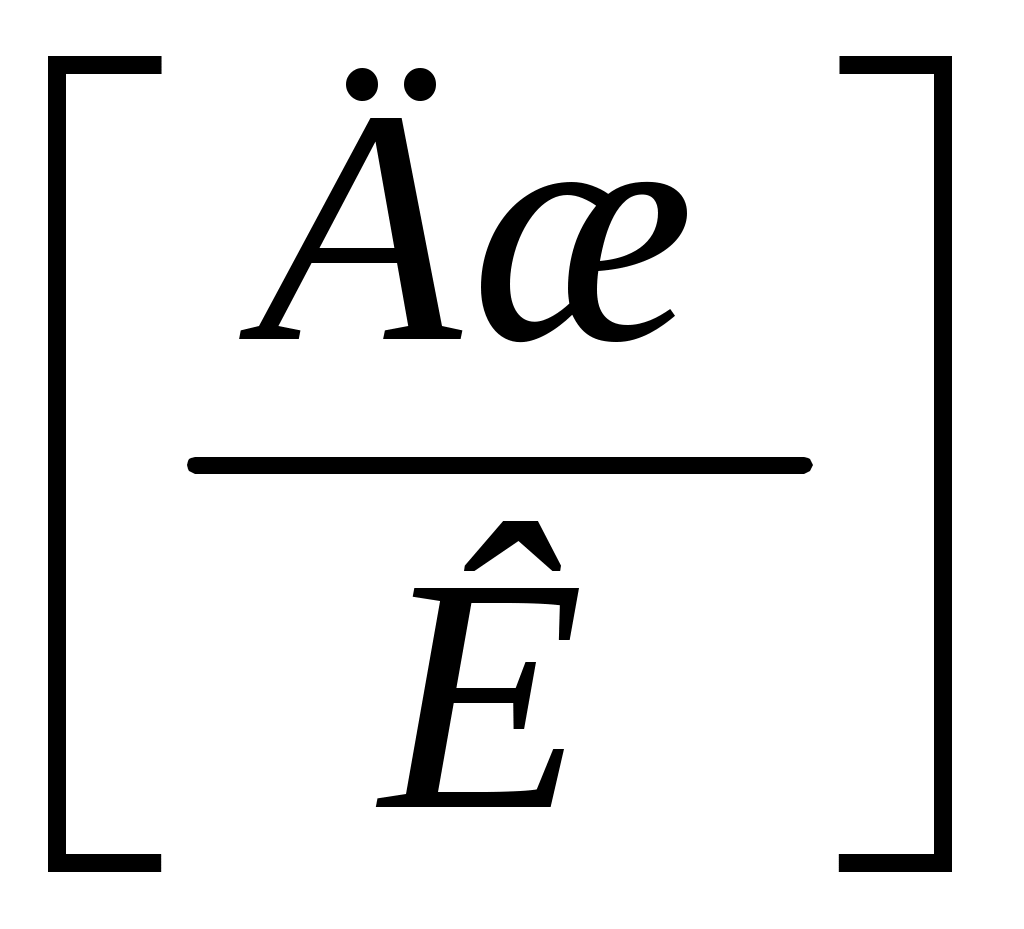(1)

Физический смысл теплоёмкости можно сформулировать проще: из определения (1) видно, что при 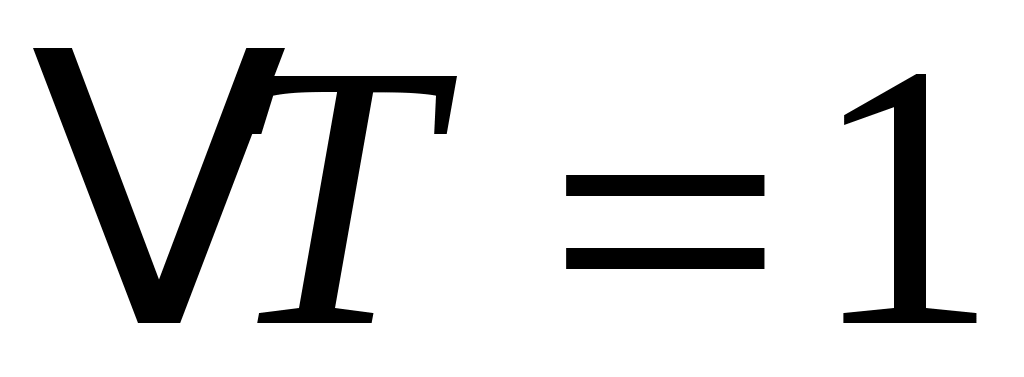теплоемкость 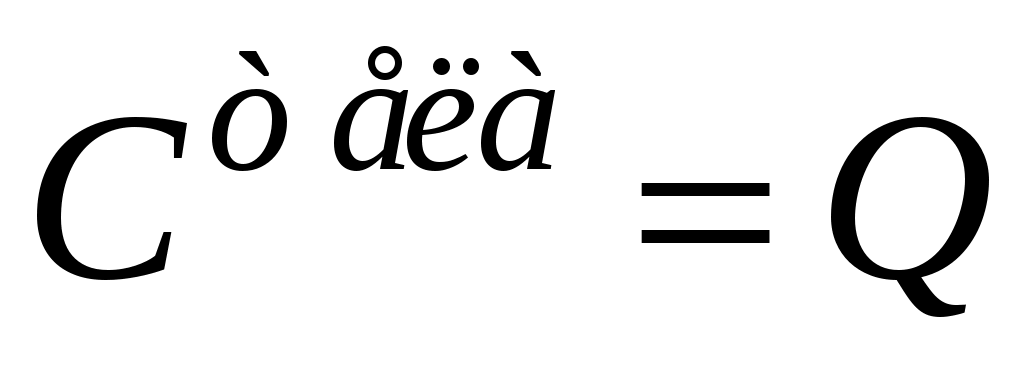; значит, теплоёмкость тела численно равна количеству тепла, которое надо сообщить телу, чтобы нагреть его на 1 градус (Кельвин). Если теплоёмкость всего тела разделить на его массу, то получим теплоёмкость единицы массы, которую называют удельной теплоёмкостью

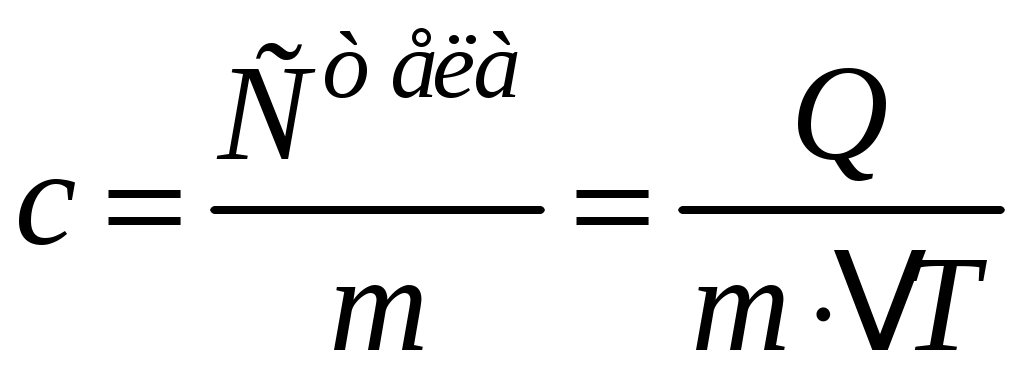
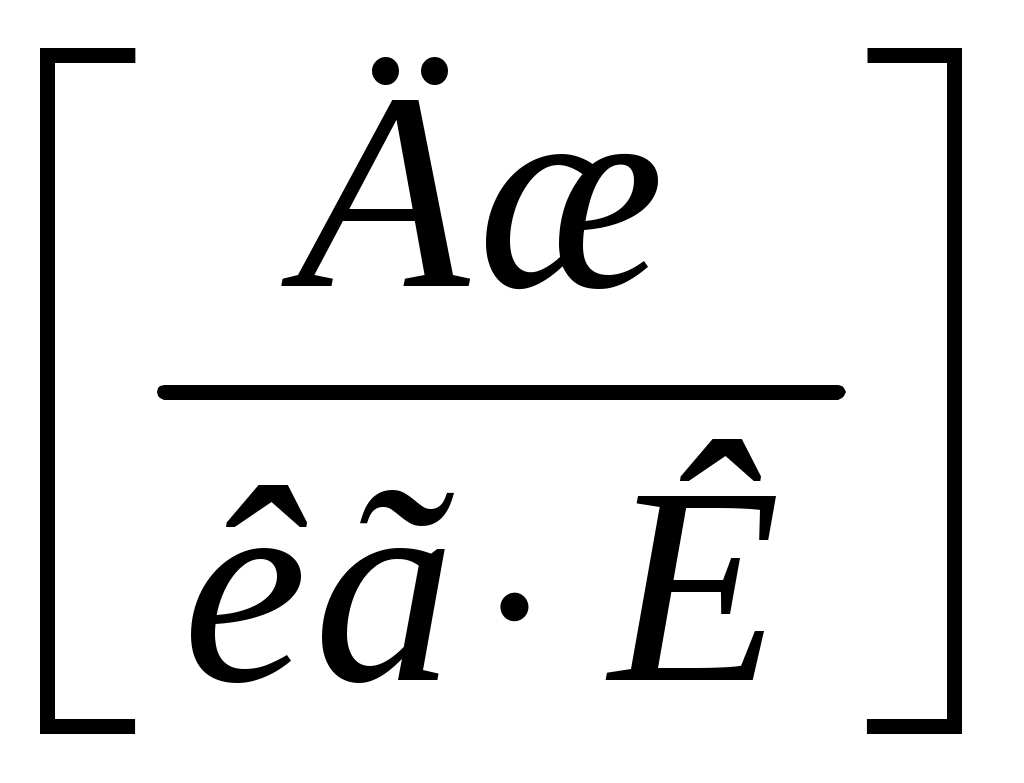. (2)

Все тела в общем случае имеют разные значения удельных теплоёмкостей, которые приводят в справочных таблицах физических констант. Зная величину c, легко посчитать количество тепла, необходимое для нагрева данного тела массой mна любое число градусов

.

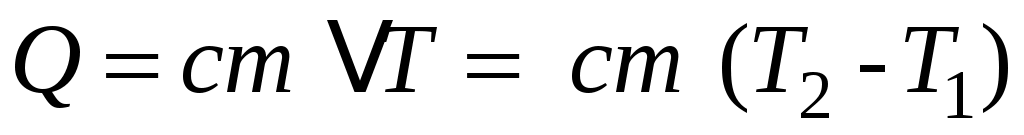Записанные выше определения являются лишь напоминанием базовых понятий, которые должны быть известны читателю из школьного курса физики.

Теперь сделаем важное уточнение. В формулах (1-2) теплоёмкость считается константой, отражающей физические свойства тела. Однако если речь идёт о газообразных телах, то для одного и того же газа эта константа оказывается различной в зависимости от того, в каком процессе нагревается газ. Это легко понять на основе также известного из школы первого закона (первого начала) термодинамики, который выражает закон сохранения энергии в наиболее общей форме и является одним из самых универсальных законов физики:

Количество тепла Q, подведённое к термодинамической системе, идёт на увеличение её внутренней энергии U и на совершение этой системой работы A против внешних сил:

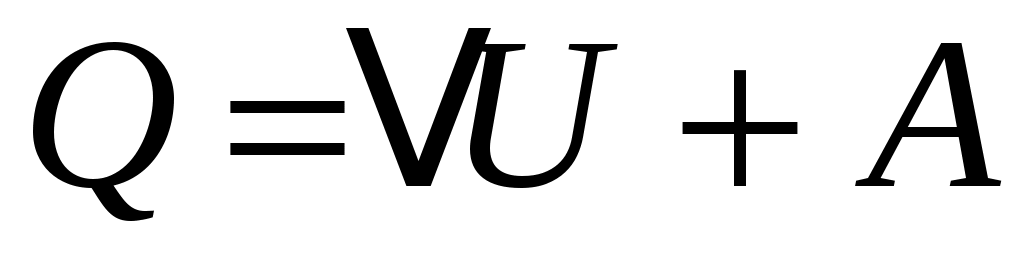, (3)

где 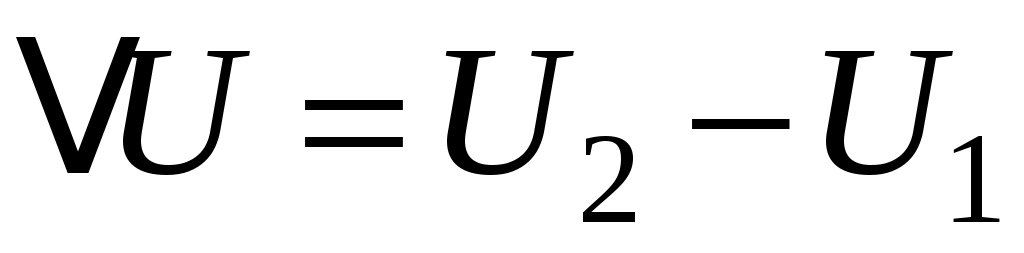_, а U₂ и U₁ – конечное и начальное значение внутренней энергии, накопленной хаотически движущимися молекулами. Здесь очень важно напомнить читателю, что внутренняя энергия идеального газа всегда строго пропорциональна его температуре (так как по определению температура и является мерой средней энергии движения молекул).

Действие закона легко представить на примере газа в цилиндре под поршнем. Если подвести к газу тепло Q, то в общем случае за счет подведения тепловой энергии он нагреется (увеличит свою внутреннею энергию U–энергию молекул) и толкнёт поршень (совершит работу A по перемещения поршня). Заметим, что газ совершает работу только когда он расширяется – когда силой своего давления перемещает внешние тела: поршень, стенки сосуда, другие массы газа и т.п., то есть когда изменяется объём рассматриваемого газа.

Сравним с позиции термодинамики два известных процесса: изохорный и изобарный. При изохорном нагреве 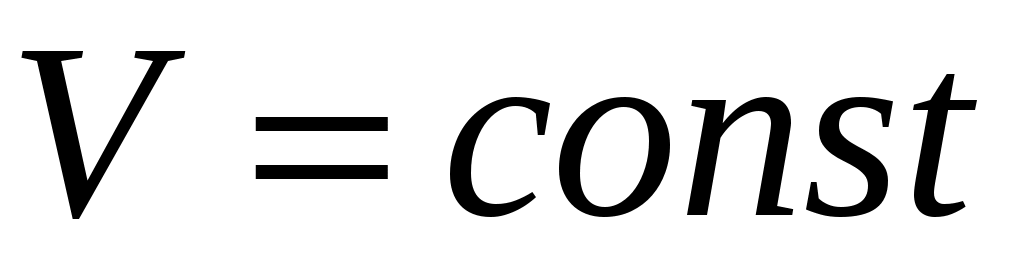, а значит, работа не совершается 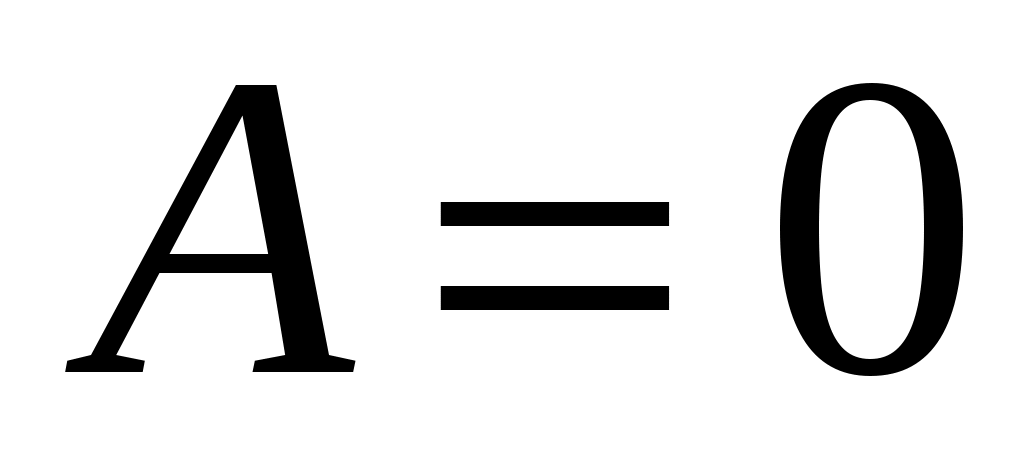, поэтому в соответствии с (3) все подведённое тепло идёт только на нагрев 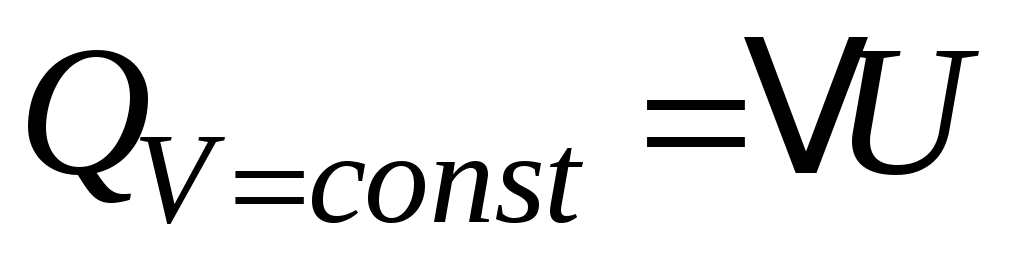, т.е. на увеличение температуры.

При изобарном нагреве давление P неизменно, а объём возрастает пропорционально температуре (закон Гей-Люссака) и газ совершает работу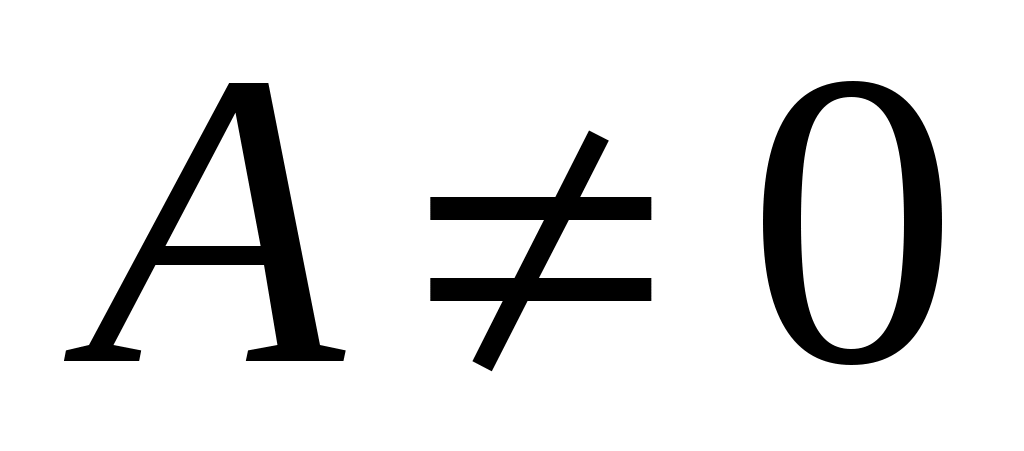 . В этом случае из всего подведённого тепла Q в соответствии с (3) только часть его идёт на нагрев газа (на увеличение внутренней энергии 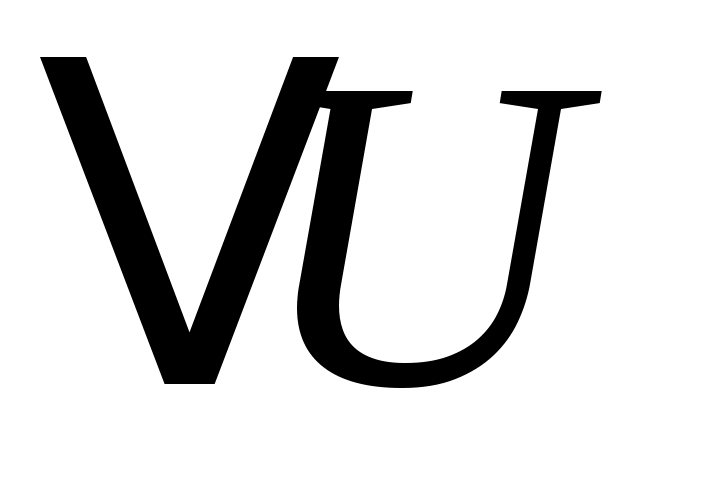), при этом .

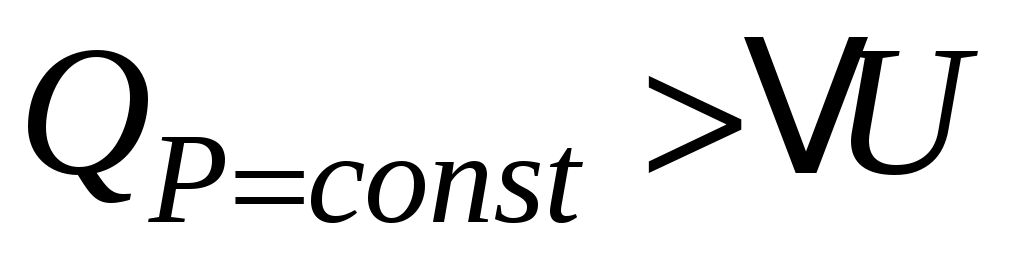Именно по этой причине для нагрева на 1 градус Кельвина при изобарном нагреве нужно к газу подводить тепла больше, чем при изохорном. Другими словами, удельная теплоёмкость любого газа при постоянном давлении с_pбольше его удельной теплоёмкости при постоянном объёме с_v, а их отношение:

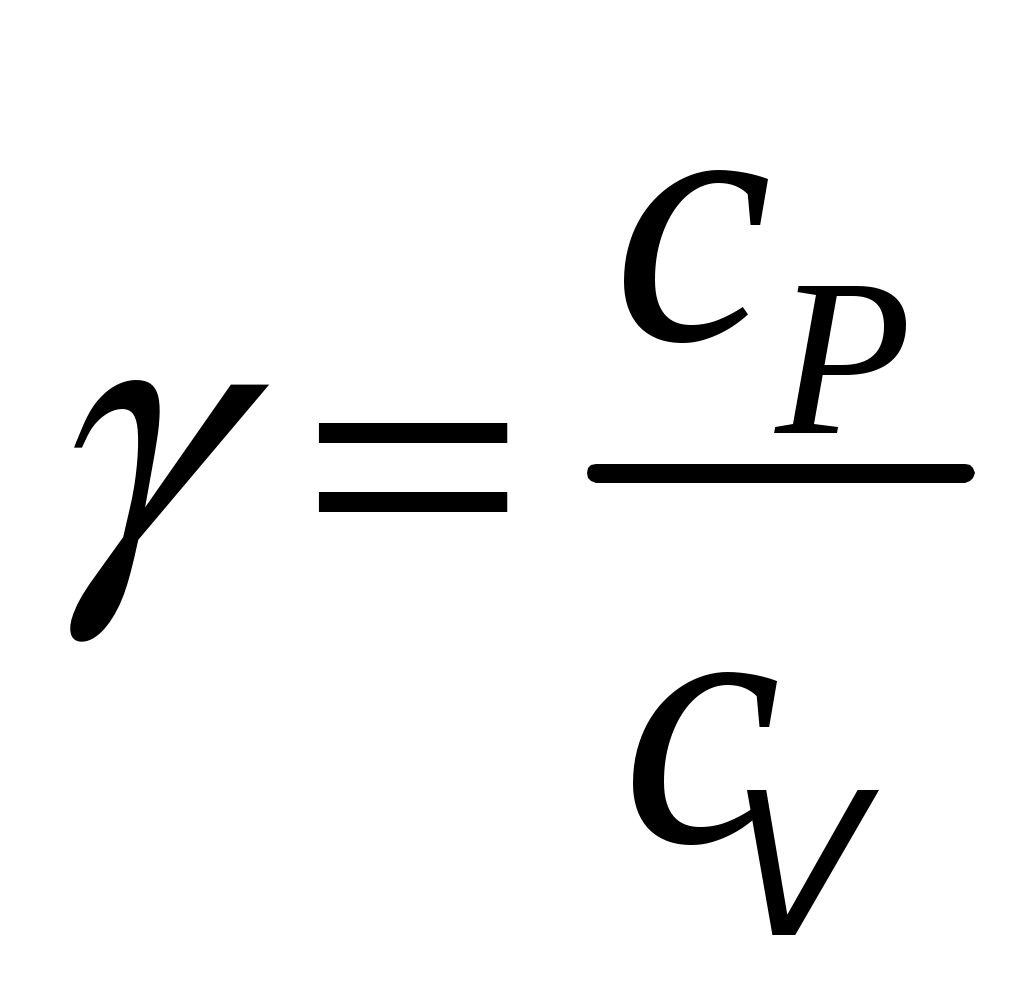(4)

всегда больше единицы. Это отношение играет в термодинамике весьма важную роль. В частности, как показывается в лекционном курсе физики, оно входит в уравнение Пуассона, которое описывает адиабатное расширение газа:

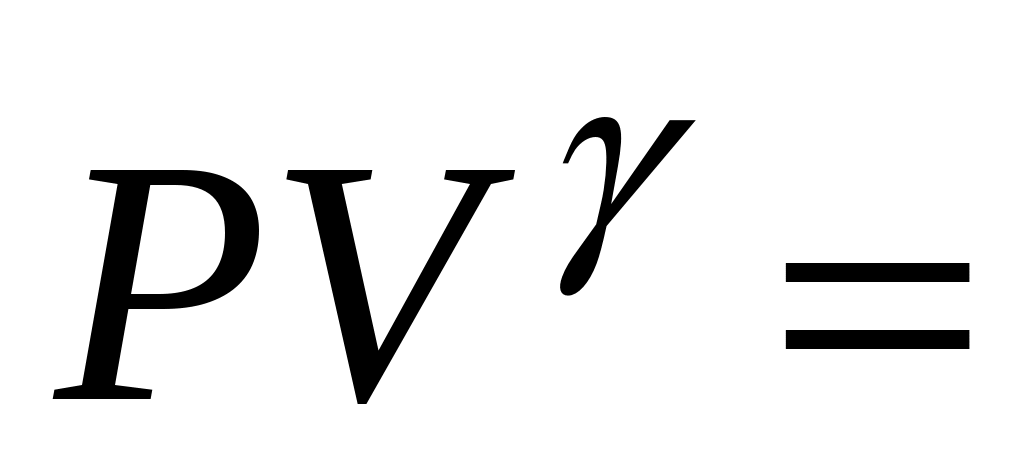const, или 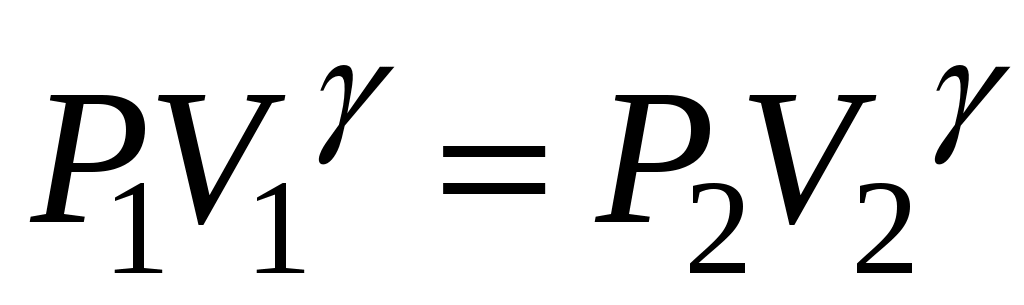, т.е. 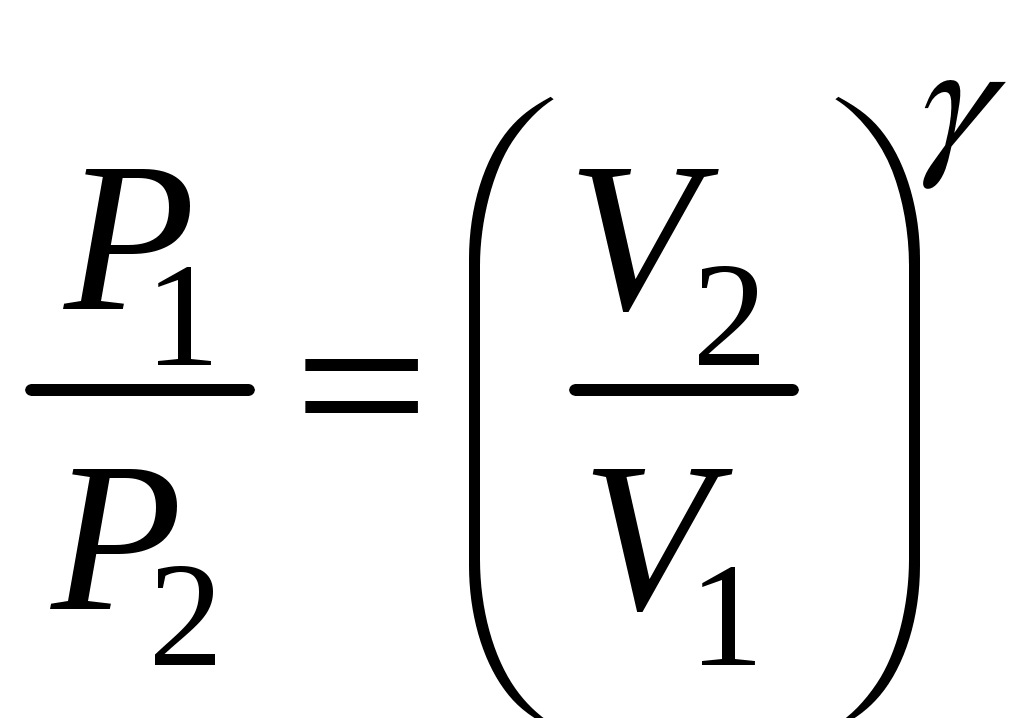– (5)

– увеличение объема приводит к резкому уменьшению давления.

Напомним, что адиабатным называется процесс, при котором теплота к газу не подводится и не отводится от него (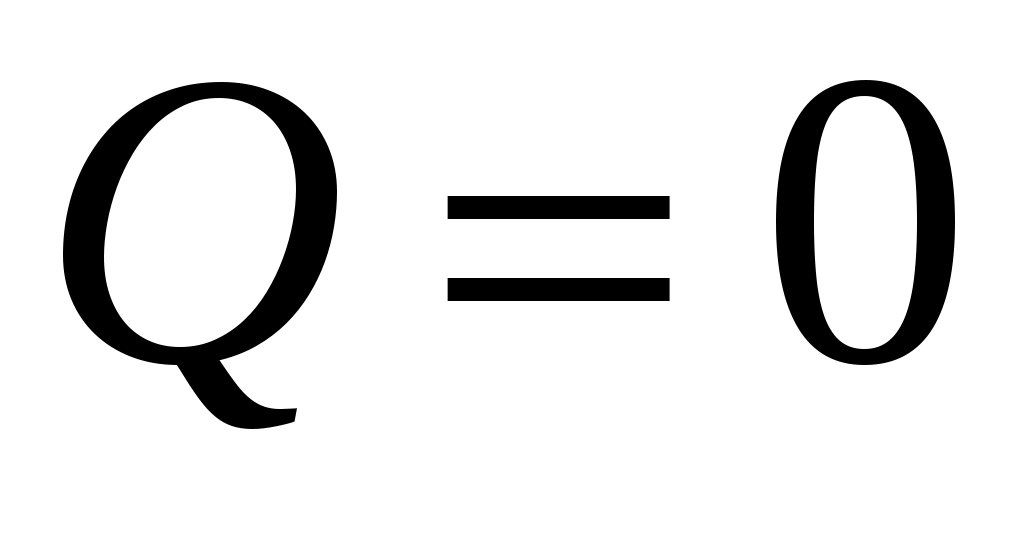 ). На практике часто быстрое расширение и быстрое сжатие газа считают именно адиабатными процессами, так как за малое время теплообмен газа с окружающей средой не успевает произойти ( ).

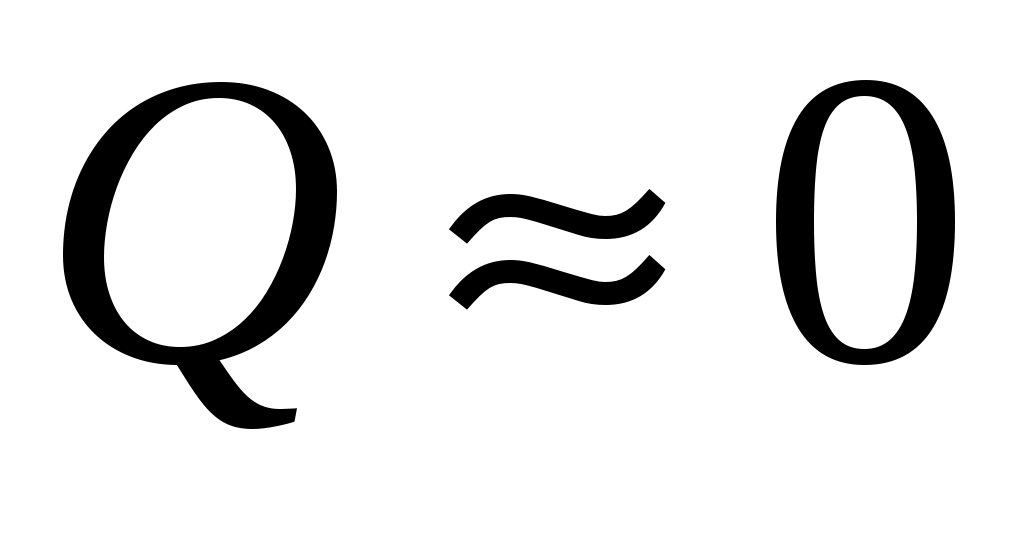Задачей данной работы и является нахождение отношения 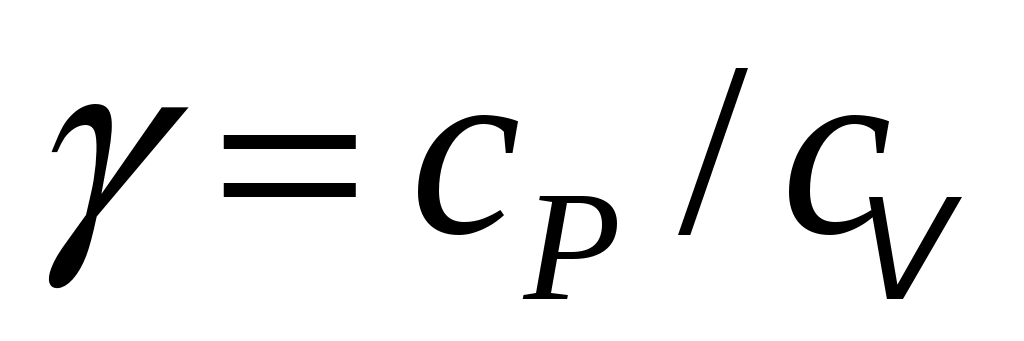для воздуха методом Клемана и Дезорма, в описании которого мы используем уравнение Пуассона и газовые законы, известные из школьного курса физики: закон Бойля-Мариотта (P₁V₁= P₂V₂при Т=const) и закон Шарля (P=const Tпри V=const).

Лабораторная установка.

Экспериментальная установка Клемана-Дезорма (рис.1) состоит из стеклянного баллона А (ёмкость около 20 л), который сообщается с трубкой В, ведущей к нагнетательному насосу и жидкостному (водяному) U-образному манометру М. Кран К₁ позволяет отсечь баллон А от насоса, а кран К₂ позволяет сообщать баллон с атмосферой.

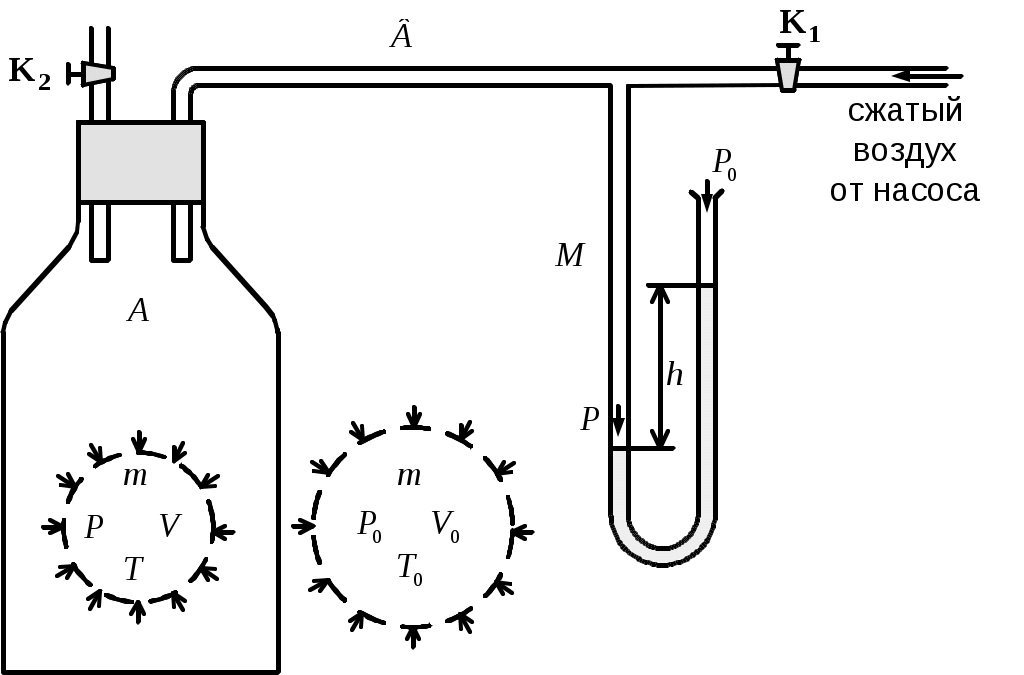
Подготовим установку к эксперименту. Для этого откроем кран К₁ и закачаем в баллон избыточный воздух (кран К₂ закрыт). Возрастание давления фиксирует манометр М. При накачке воздуха температура его повышается. Это объясняется тем, что силы, прилагаемые к поршню насоса, совершают работу по сжатию газа в баллоне, и средняя энергия молекул, а следовательно, и температура газа в баллоне возрастает. Достигнув перепада высот h в манометре порядка 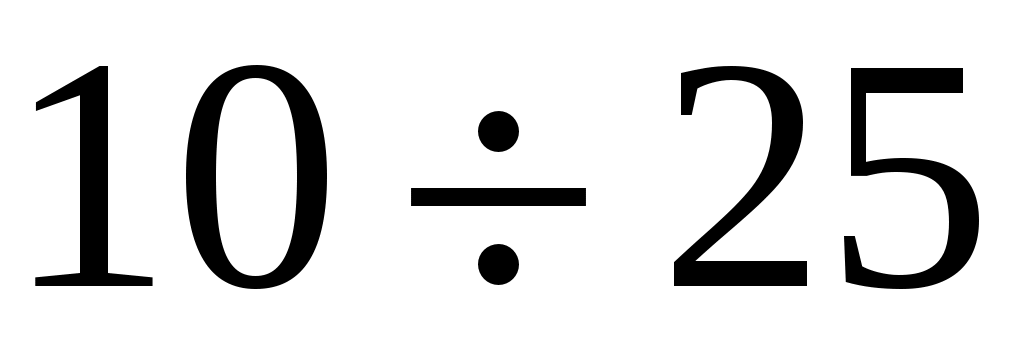см водяного столба, перекроем кран К₁.

Б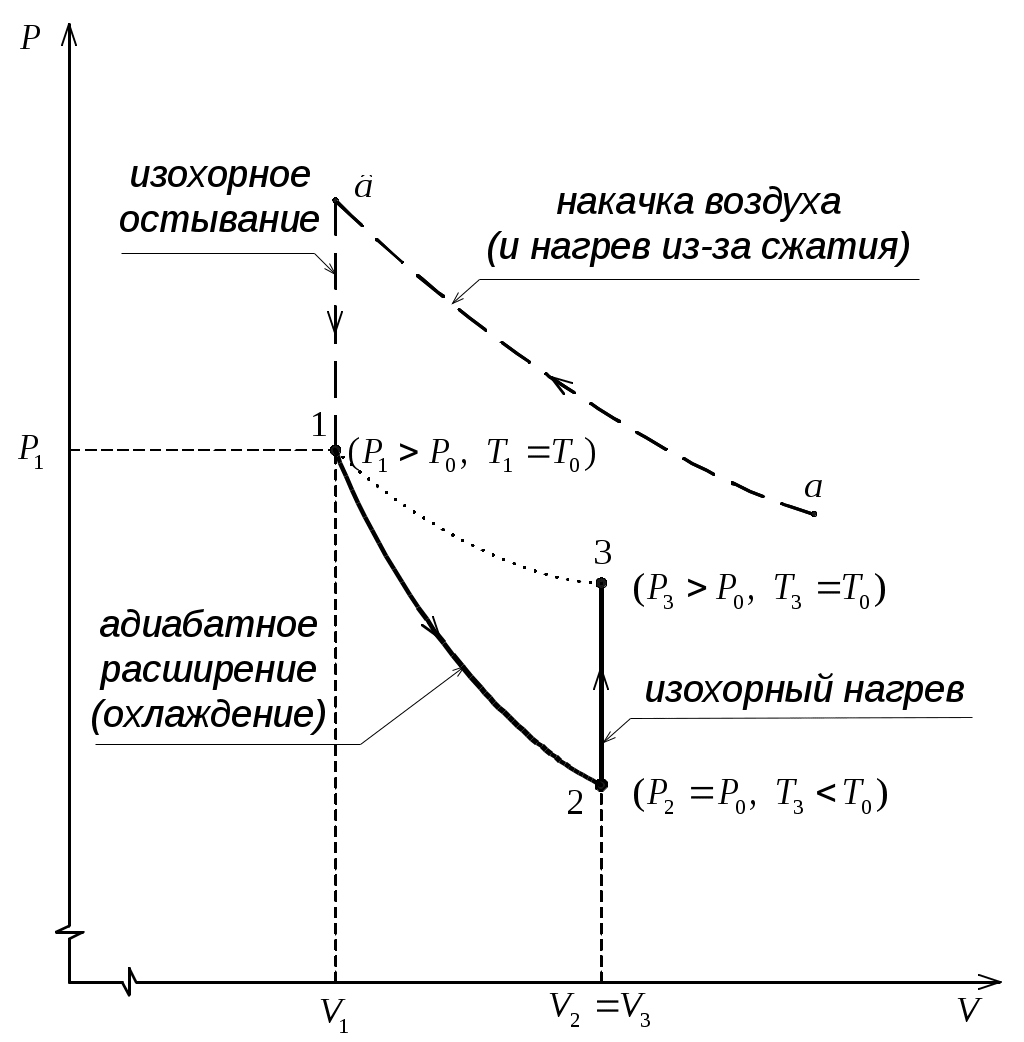 удем мысленно следить за некоторой массой m воздуха внутри баллона. При накачивании в баллон избыточного воздуха давление P и температура T рассматриваемой порции газа возрастают относительно P₀и T₀ – параметров окружающей среды (комнаты), а объем V – уменьшается (газ сжат). Этот процесс накачки можно изобразить кривой на диаграмме P-V (рис. 2). После перекрывания крана К₁ газ оказывается в точке 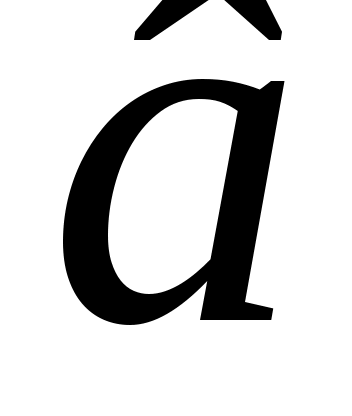. Поскольку газ нагрет ( 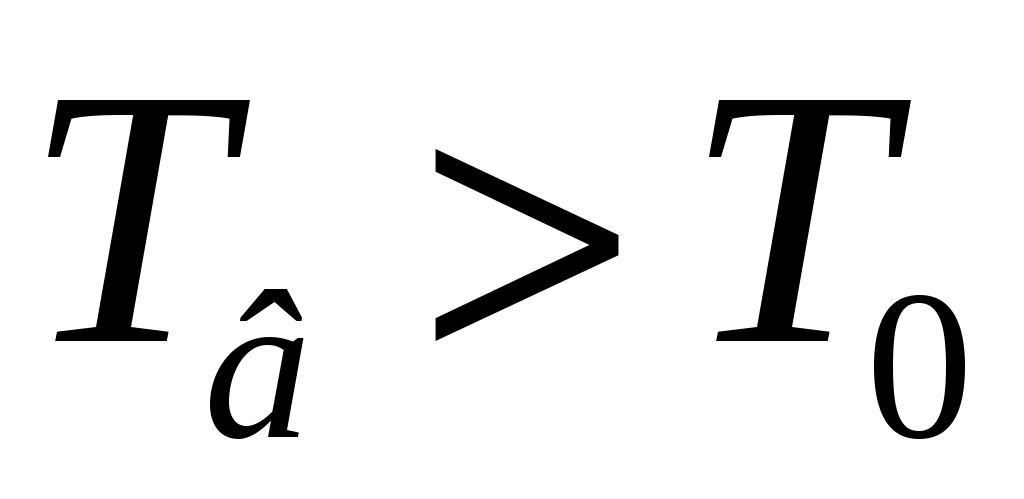), а стенки баллона обладают определённой теплопроводностью, то газ начинает постепенно остывать пока температура его не сравняется с комнатной. Это изохорное охлаждение ( 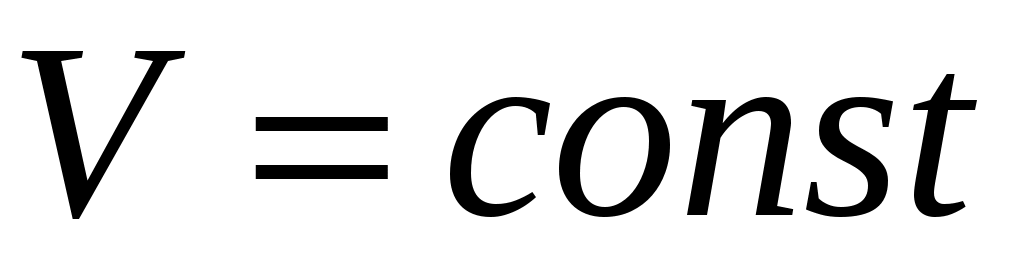) на рис.2 изображено линией 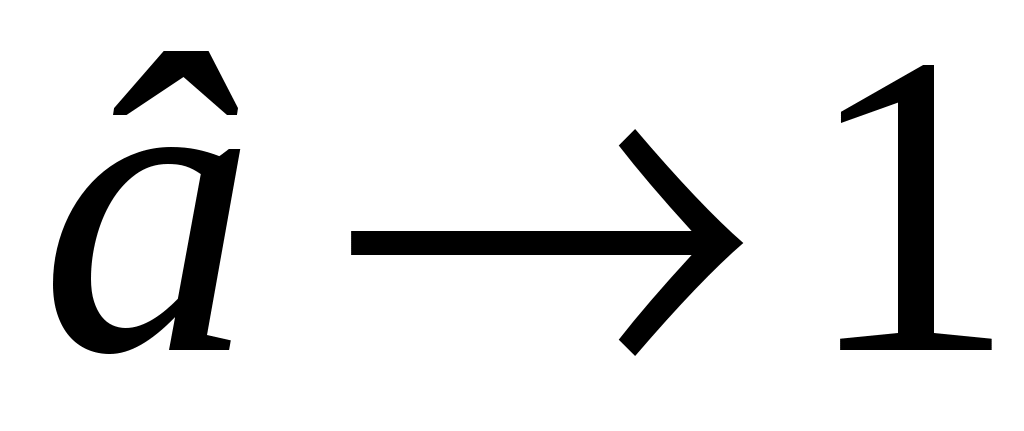. Изохорное охлаждение по закону Шарля (P пропорционально T) сопровождается уменьшением давления и на установке это наблюдается по уменьшению столба жидкости h в манометре. Когда уровень жидкости в манометре перестанет снижаться, точка 1 достигнута. Это начальная точка для экспериментальных измерений. В ней P₁>P₀, T₁=T₀. Измерим это установившееся давление с помощью манометра 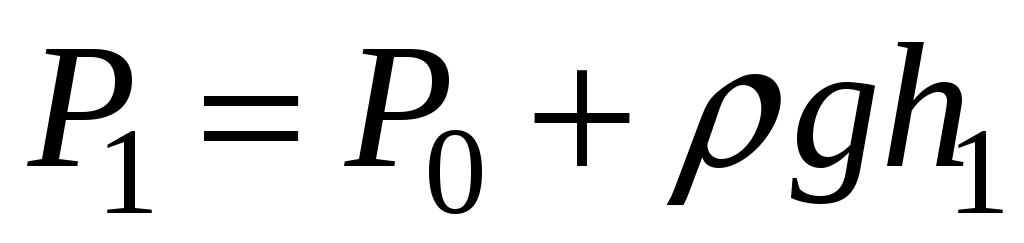, где 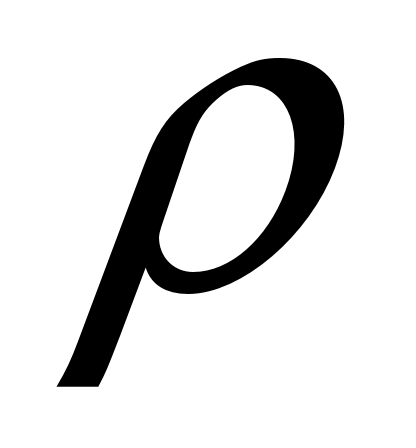– плотность жидкости в манометре,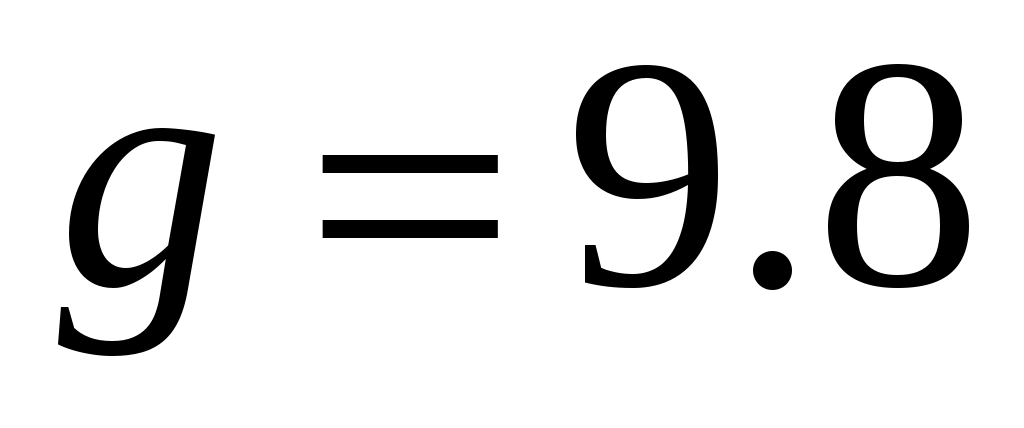 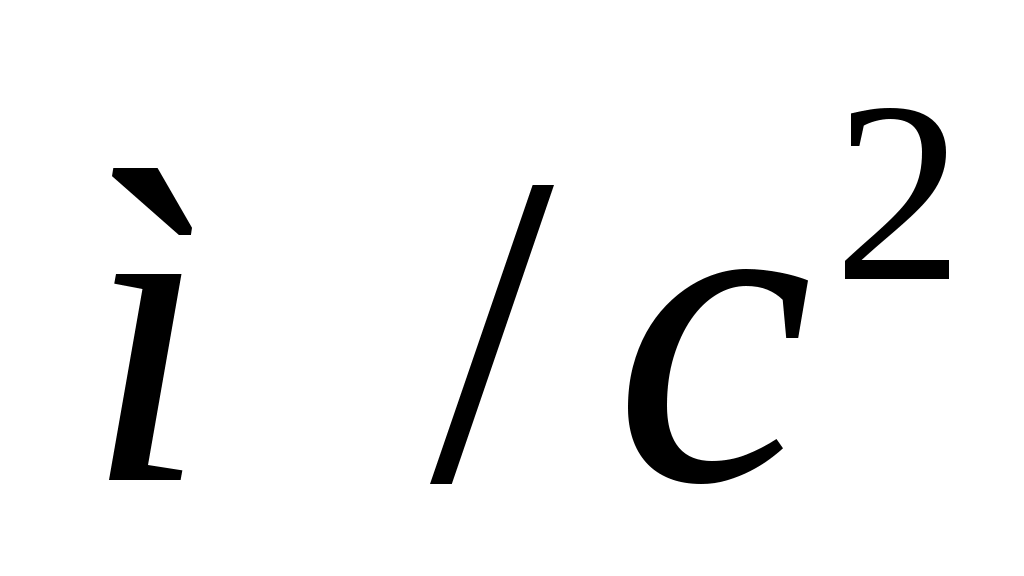– ускорение свободного падения ( 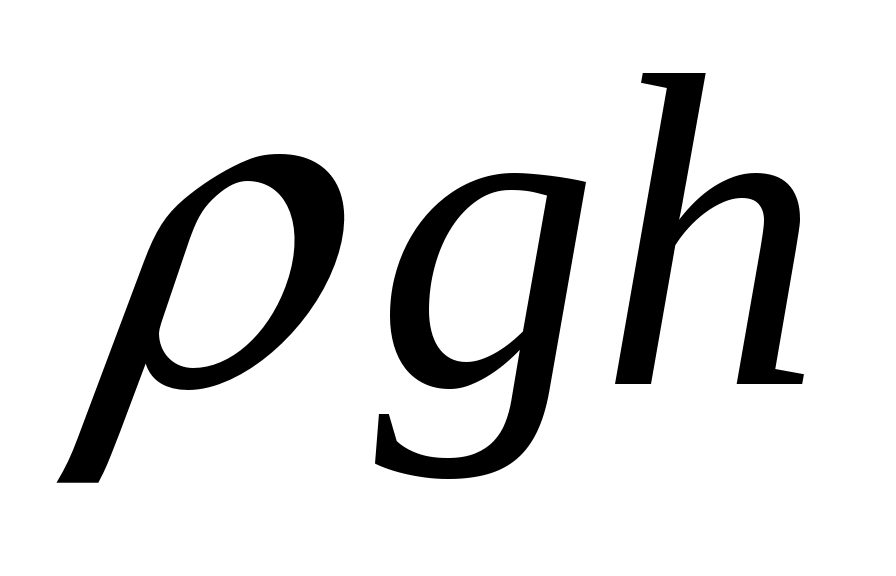– избыточное давление, равное давлению столба воды). Запишем значение h₁.

Эксперимент далее состоит в том, что кран К₂ открывают на короткий промежуток времени (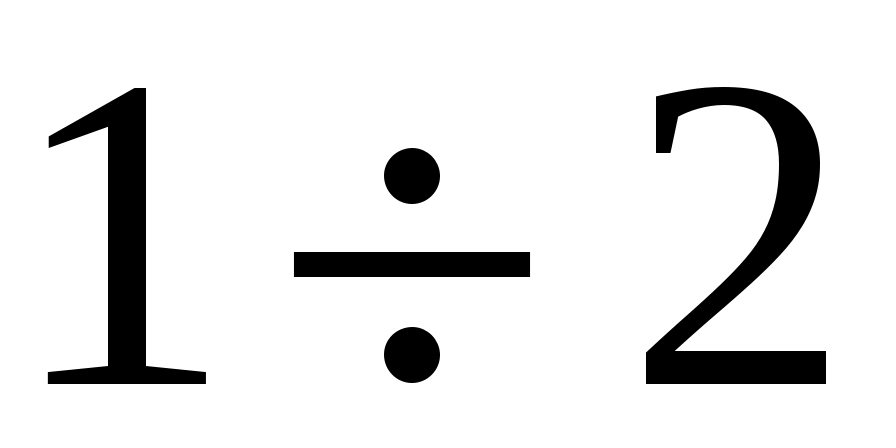 секунды) и снова его закрывают.

Пока кран К₂ открыт, происходит резкий выхлоп избыточного воздуха и давление сравнивается с наружным 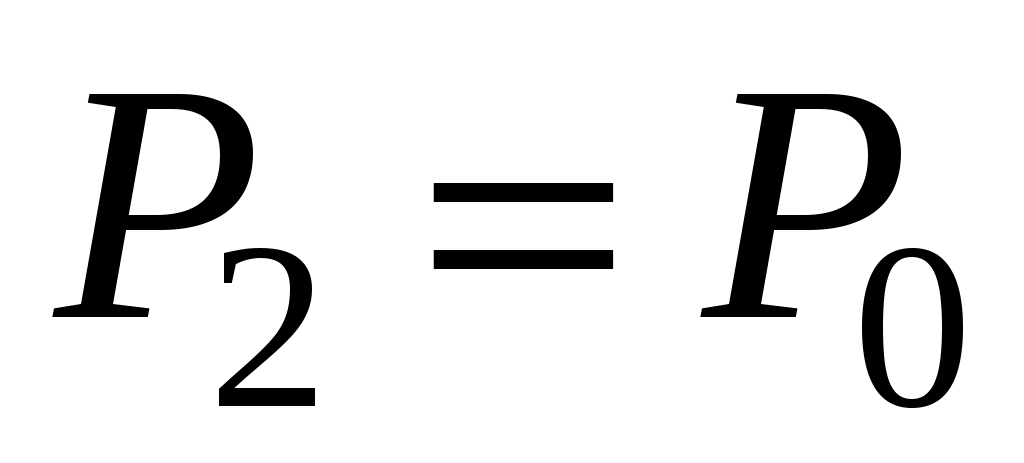. Поскольку этот процесс происходит очень быстро, то теплообмен между воздухом в баллоне и окружающей комнатной средой не успевает произойти ( 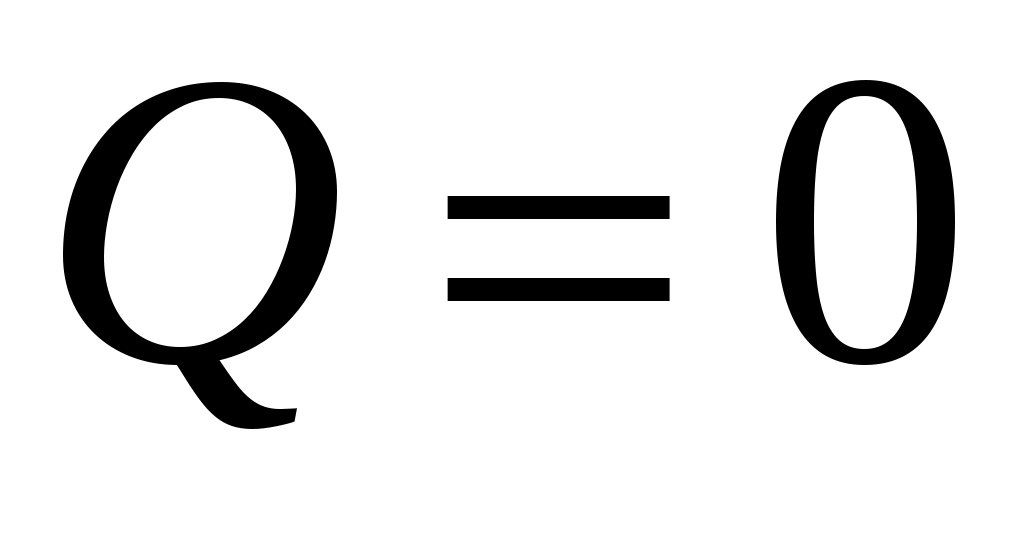), и такой процесс быстрого расширения газа можно считать адиабатным. Он подчиняется уравнению Пуассона (5): 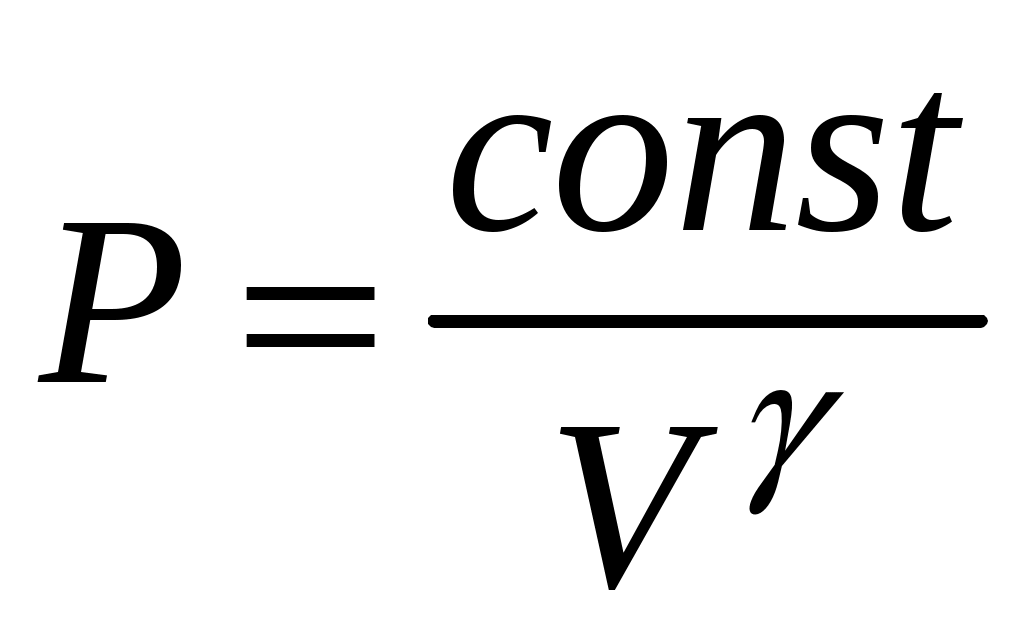- эта зависимость на рис.2 изображена падающей кривой 1→2. В процессе резкого адиабатного расширения воздух охлаждается (работа расширения совершается за счет убыли внутренней энергии по формуле (3) 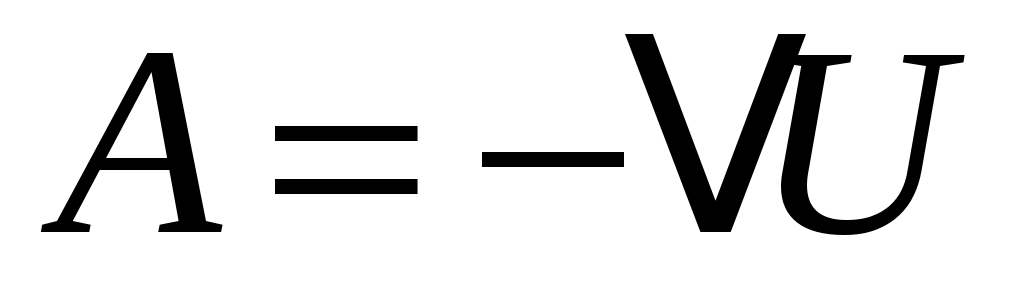, так как 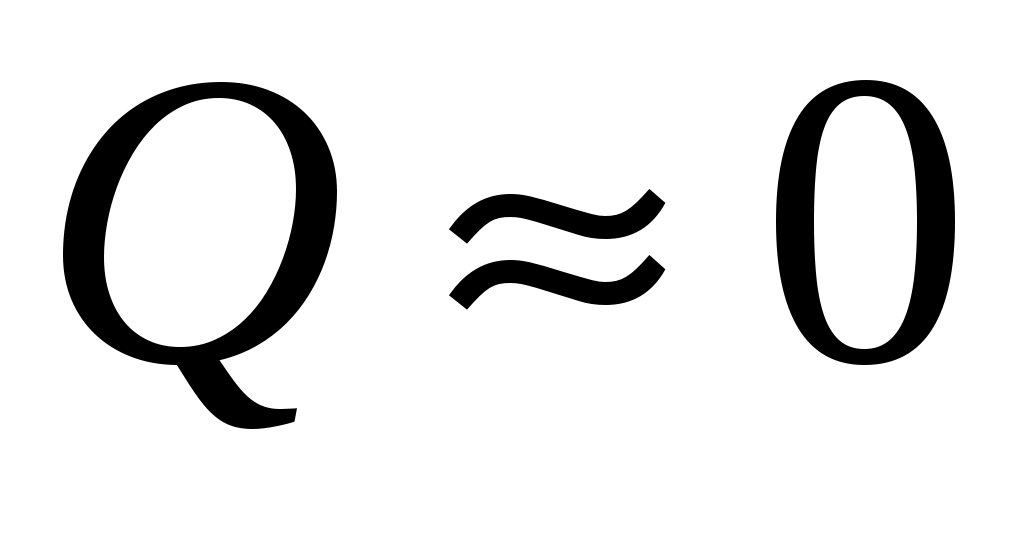). В конце адиабатного расширения (в точке 2, в которой кран К₂ перекрывается) температура газа T₂ становится, таким образом, ниже комнатной 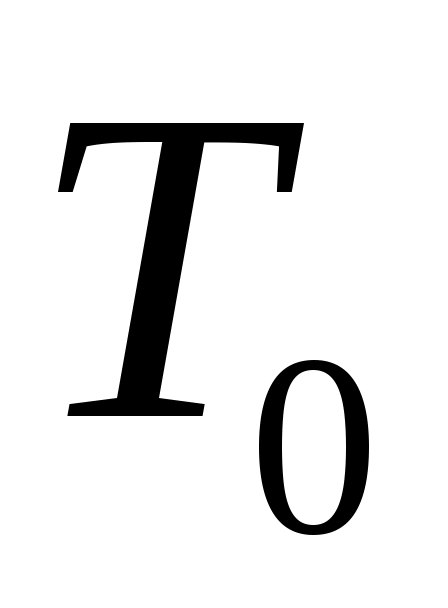, а давление выравнивается с атмосферным 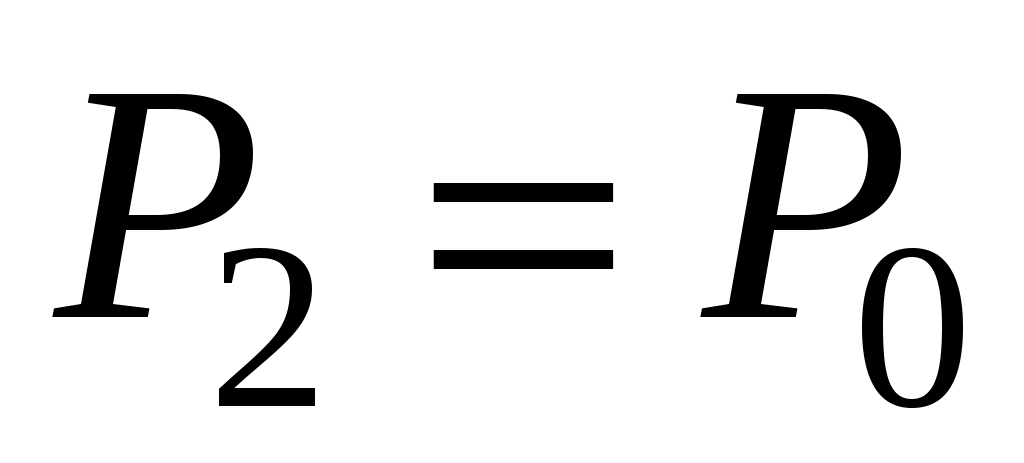, что фиксируется манометром, который в этот момент показывает h=0.

Далее после перекрытия К₂ охлажденный в баллоне воздух благодаря теплопроводности стенок постепенно нагревается до комнатной температуры. Это изохорный нагрев (участок 2-3 на рис.2), в результате которого давление также постепенно возрастает. В точке 3 температура сравнивается с комнатной 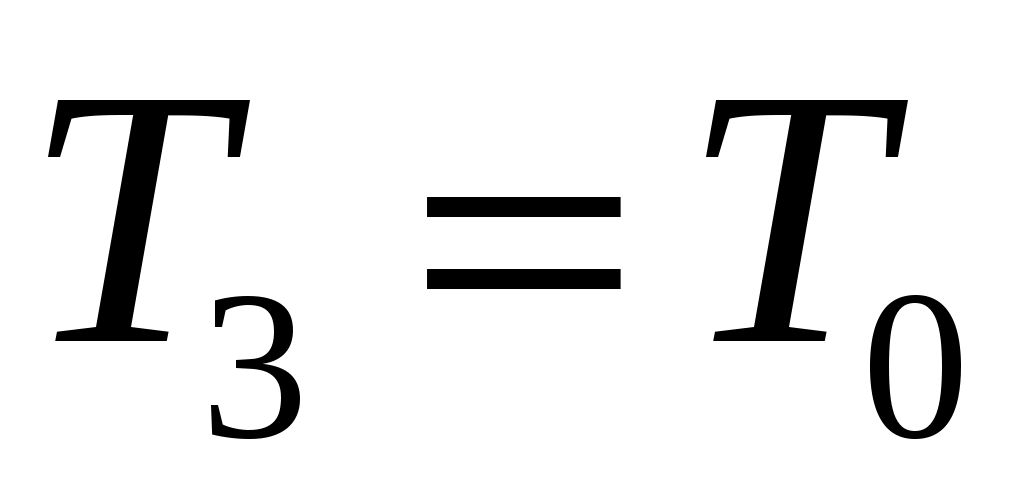, и давление достигает значения 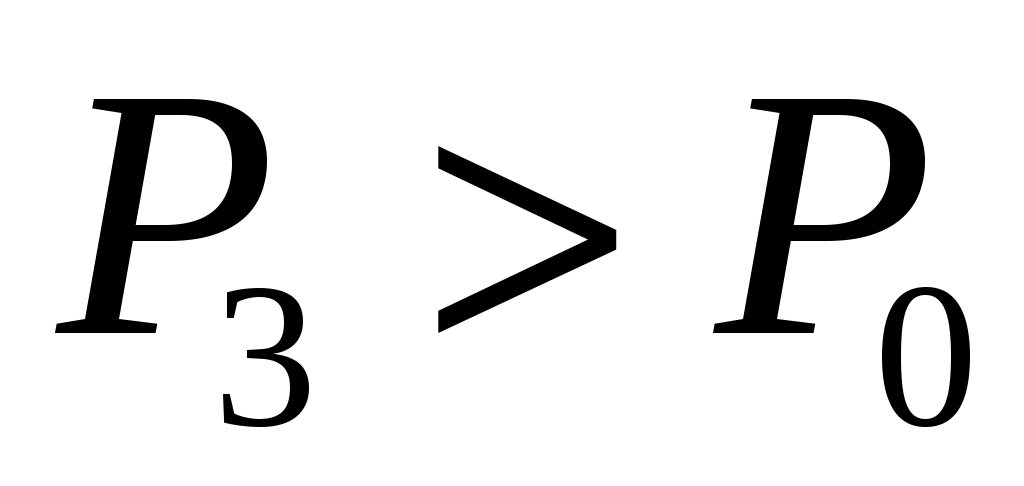. Это давление также фиксируется манометром: 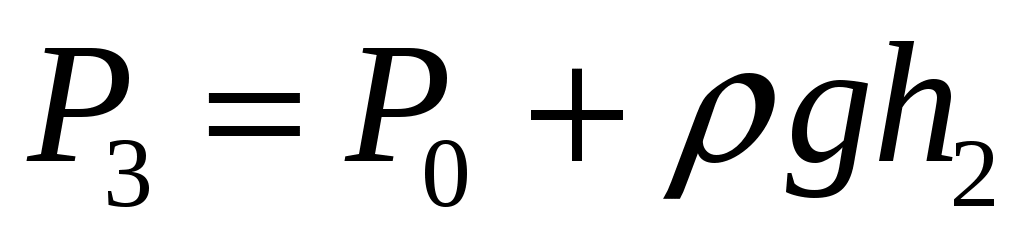, где h₂ – конечный перепад уровней воды в манометре, который также следует записать.

Оказывается, по начальному перепаду уровней h₁ и конечному h₂ можно легко вычислить искомое отношение 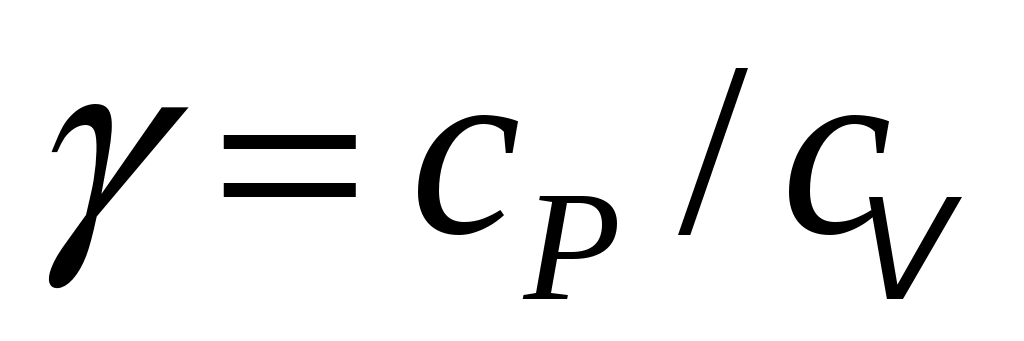для данного газа (воздуха):

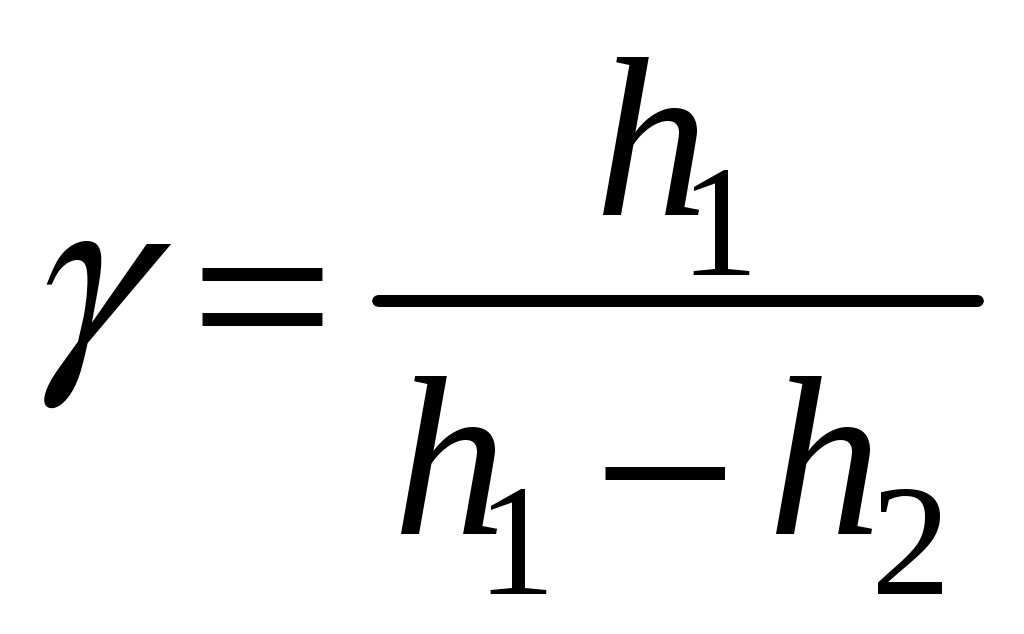(6)

Обоснуем эту простую формулу, рассматривая рабочие этапы графика 1-2-3 с помощью известных газовых законов. Между состояниями 1 и 2 (рис.2) идёт адиабатный процесс. По уравнению Пуассона (5) запишем:

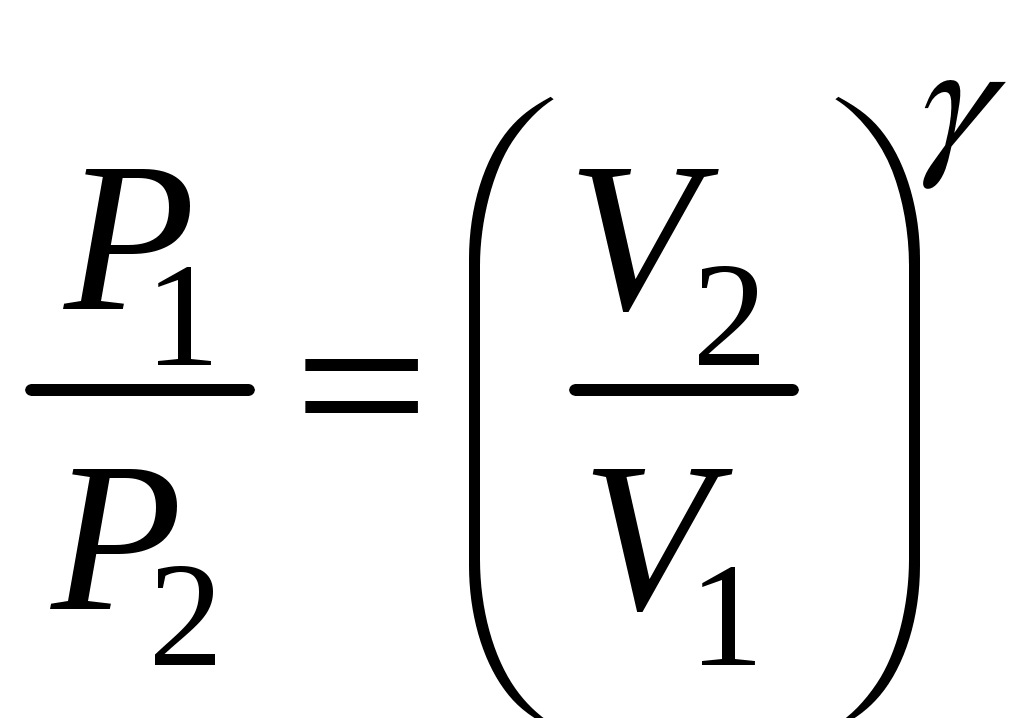(7)

Состояние 1 и 3 оказываются при одинаковой температуре Т₁= Т₃= Т₀, и следовательно, связаны законом Бойля-Мариотта

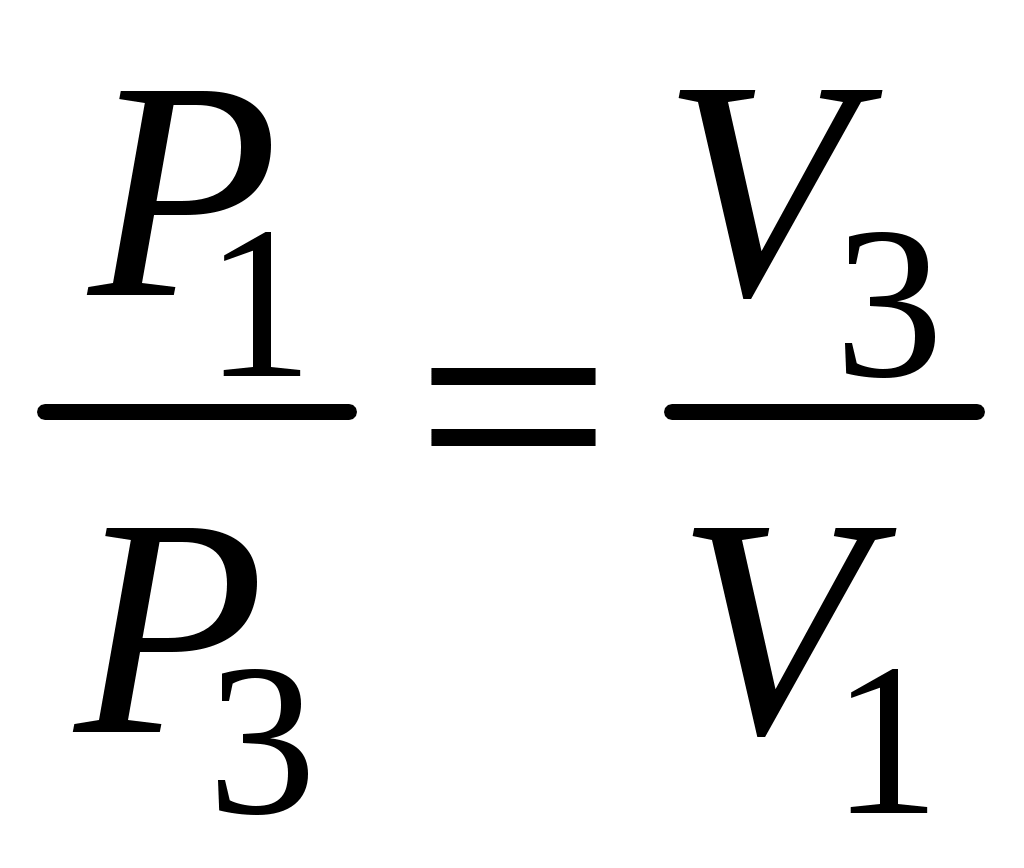(8)

Заметим, что в этом эксперименте изотермического процесса нет, но точки 1 и 3 лежат на краях мысленной изотермы, которая для наглядности проведена на рис.2 пунктиром.

Поскольку V₃=V₂, то возведя (8) в степень 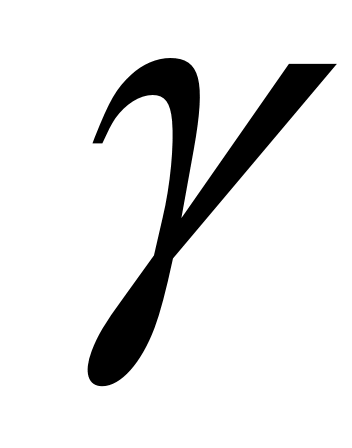, мы получим равенство правых частей (8) и (7). Приравняв левые части, получим:

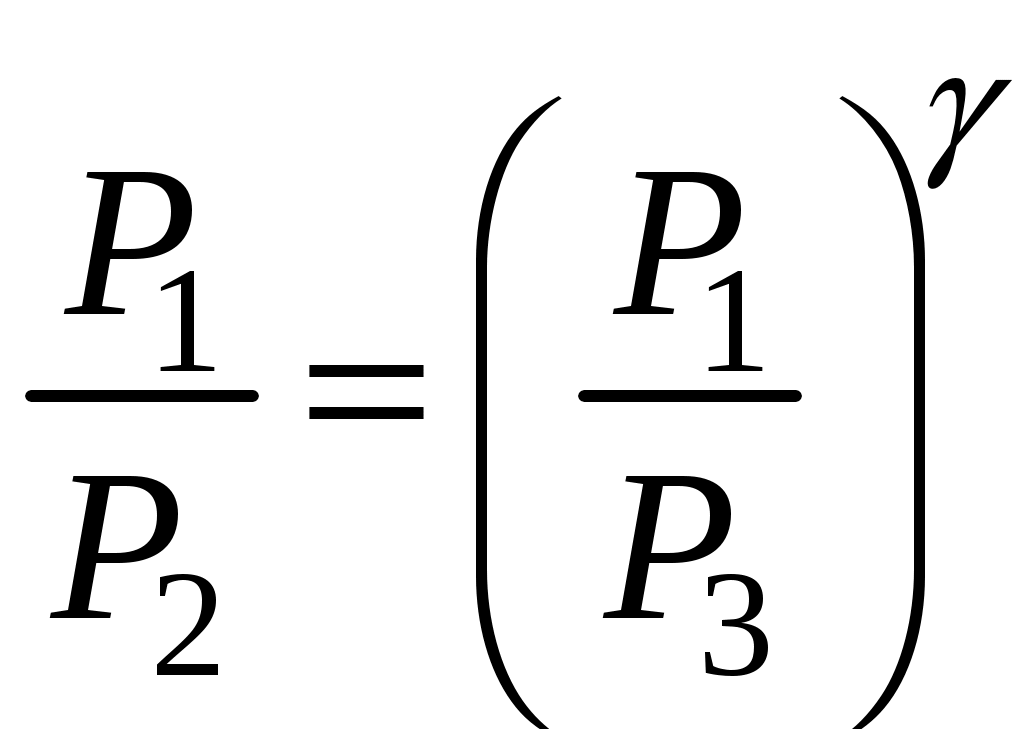(9)

Отсюда, измеряя только давления, можно определить γ. Приведём формулу (9) к виду (6). Для этого прологарифмируем (9):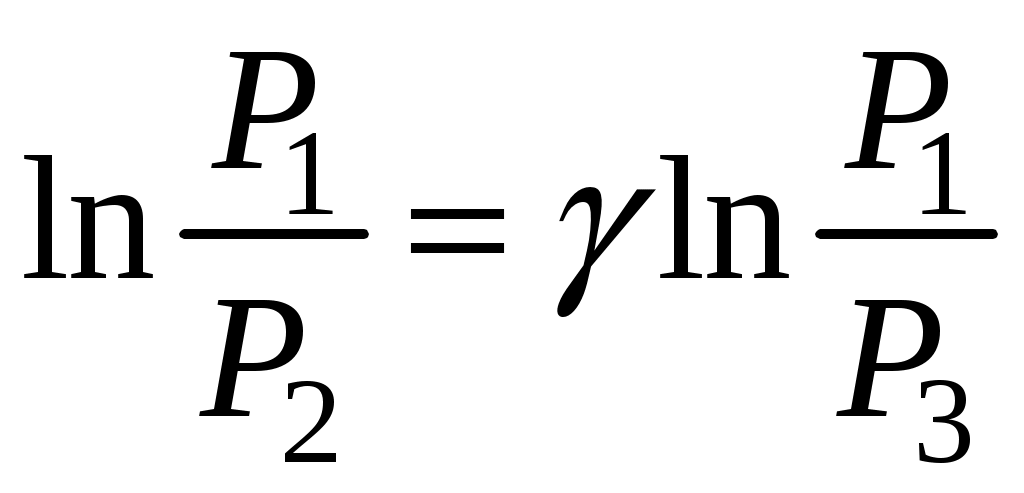

и найдём 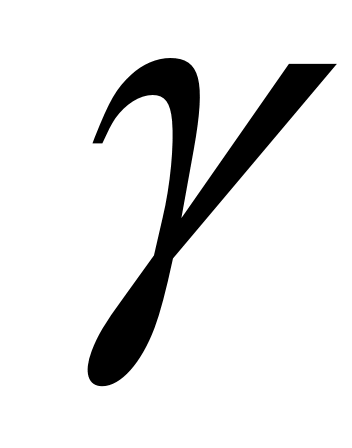, выражая P₁, P₂, P₃ через P₀, h₁, h₂,

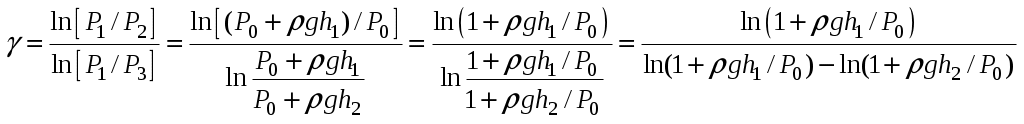В математике есть простое правило: если х << 1, то ln(1+x) 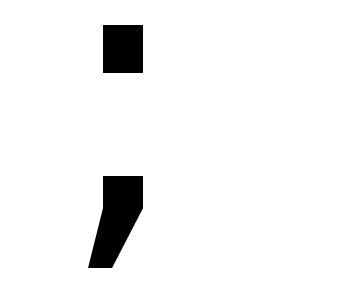x. В этом можно убедиться с помощью калькулятора. Например, ln 1.02 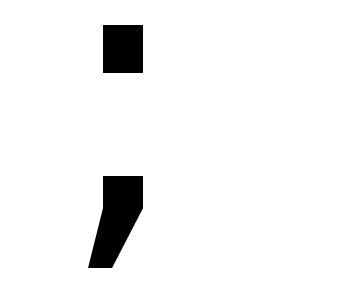0.02 и т.п.

В нашем случае все дроби вида 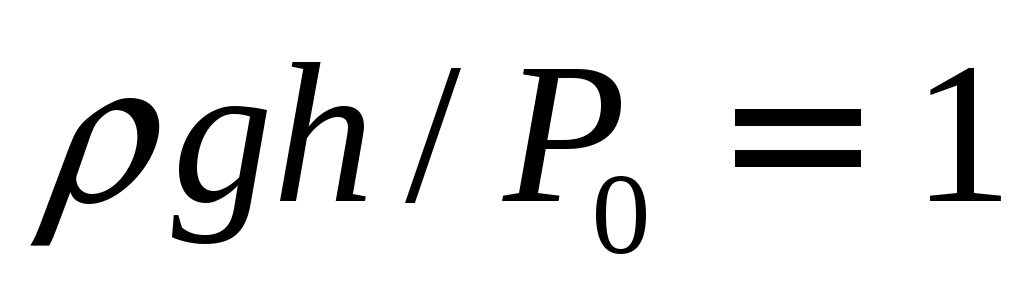, т.к. давление ρgh – это давление порядка 0.2 м водяного столба, а P₀ – атмосферное давление порядка 10 м водяного столба, как известно из начального курса школьной физики.

Поэтому с хорошей точностью можно записать



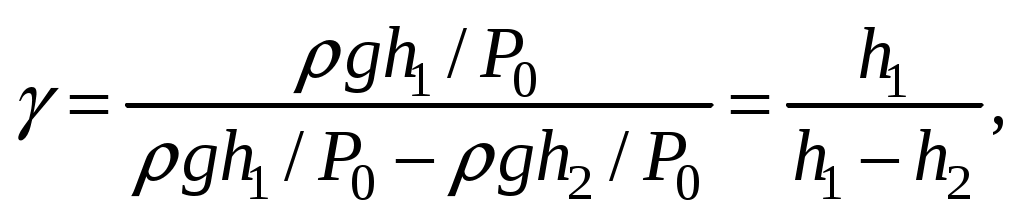
что и требовалось доказать. Мы получили рабочую формулу (6).
Порядок выполнения работы.

1. Открыть кран К₁ и с помощью насоса (компрессора) накачать в баллон воздух до избыточного давления в пределах

25см водяного столба, контролируемого манометром.

---

2. Закрыть кран К₁ и следить за понижением уровня в манометре (идёт изохорное охлаждение газа до комнатной температуры).

3. Когда уровень перестанет понижаться, записать величину h₁.

4. Открыть кран К₂ на секунды, чтобы произошел адиабатный выхлоп избыточного воздуха, и снова закрыть кран К₂ (обратить внимание, что во время выхлопа, избыточное давление падало до нуля, h=0).

5. Наблюдать за повышением давления после закрытия крана К₂ (идёт изохорный нагрев охлаждённого газа до комнатной температуры). Записать максимальный подъём уровня жидкости в манометре h₂.

6. По формуле (6) вычислить отношение для воздуха.

7. Повторить опыт (пункты 1-6) не менее 5 раз. Все данные записать в таблицу.

Номер опыта	h1	h2	γi	∆γi	γ	∆γ
	мм	мм
1 5

8. Усреднить результат

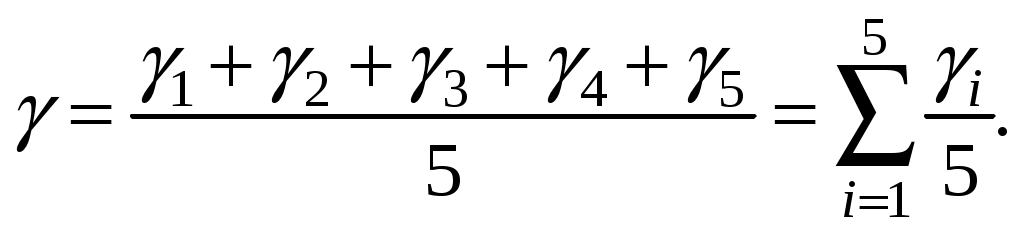(10)

9. Определить стандартную ошибку отдельных значений γ_i., по формуле



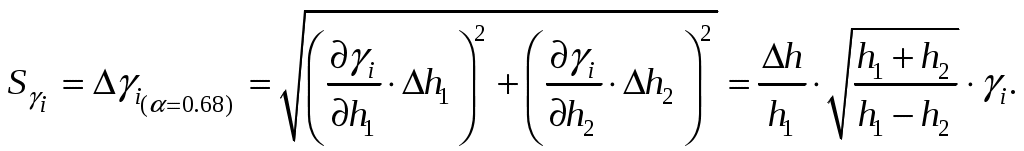
Здесь учтено, что , так как в обоих случаях это есть ошибка миллиметровой шкалы манометра.

10. Поскольку окончательно γ определяется по формуле (10), найдём стандартную ошибку усреднённого результата (с вероятностью 68%)



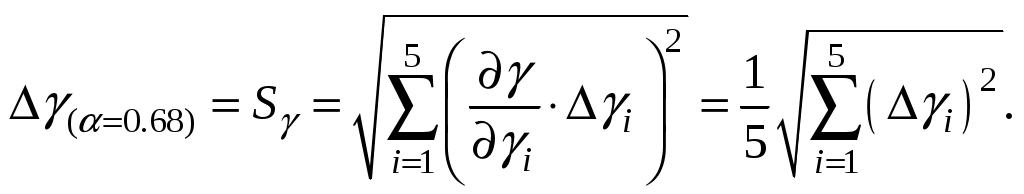
11. Записать окончательный результат и сделать выводы.

---

Контрольные вопросы.

1. Что называется теплоёмкостью тела? Удельной теплоёмкостью?

2. Сформулировать первое начало термодинамики

3. Какая теплоёмкость газа выше: или и почему?

4. Что такое адиабатный процесс? Написать уравнение Пуассона. Изобразить график адиабатного процесса.

5. Изобразить схему установки Клемана-Дезорма для определения отношения теплоёмкостей газа . Перечислить последовательно все операции одного цикла опыта с указанием типов термодинамических процессов газа на каждом этапе.

6. Изобразить все процессы одного цикла на диаграмме P-V.

7. Вывести расчетную формулу для определения величины .

8. Почему состояния в начале адиабатного процесса и в конце изохорного нагрева связаны законом Бойля-Мариотта?

9. Вывести формулу для расчета погрешности величины .

Литература

1. Трофимова Т.И. Курс физики. М.: Высш. шк., 2008.

2. Руководство к лабораторным работам по физике (под редакцией Гольдина Л.Л). М.: Наука, 1973.

---

Смотрите также файлы

• Задачи на смеси, сплавы, растворыКондратьев Иван.docx

• Млекопитающие.docx

• Реферат ученика 11б класса Полякова Виктора.docx

• Технология моделирования транспортной инфраструктуры.docx

• Реферат по дисциплине Философские проблемы науки и техники на тему Эпоха Возрождения как подготовительный этап к обоснованию новой науки. Гуманизм и самореализация творческой личности.pdf