МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА» (РУТ (МИИТ)
РОССИЙСКАЯ ОТКРЫТАЯ АКАДЕМИЯ ТРАНСПОРТА _____________________________________________________________________________
Практическая работа №1

По дисциплине: «Теория вероятностей и математическая статистика»

Выполнил:

студент 2 курса

группы ЗБЭ-2912

Ткач А.А.

Шифр:

1910-п/ЭБс-0510

Проверил: Карпухин В.Б.

Москва 2020
КОНТРОЛЬНАЯ РАБОТА
ЗАДАЧА 1

10. 
    Вероятность поражения стрелком мишени при одном выстреле равна 0,8. Найти вероятность того, что при пяти последовательных выстрелах будет не менее четырех попаданий.
    

Решение:


Найдем ряд распределения X.
Здесь λ = np = 5*0.8 = 4
P(0) = e^{- λ} = e^-4 = 0.01832
P(1) = λ*e^-λ = 4e^-4 = 0.07326




Найдем вероятность того, что событие наступит не менее 4 раз.
P(X ≥ 4) = 1-(0.01832 + 0.07326 + 0.1465 + 0.1954) = 0.5665

Ответ: 0.5665
ЗАДАЧА 2
Задана функция распределения вероятностей F(x) непрерывной случайной величины Х.

20.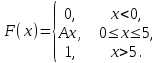

 = 2,  = 4.

---

Требуется:

1. 
   найти функцию плотности распределения вероятностей f(x);
   
2. 
   найти коэффициент А;
   
3. 
   схематично построить графики F(x), f(x);
   
4. 
   найти математическое ожидание и дисперсию Х;
   
5. 
   найти вероятность того, что Х примет значение из интервала (,
   

).

Решение:

1. 
   Найдем плотность распределения f(x), как производную от функции распределения F(x):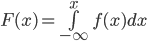
   
   

F(x) = 1, x > 5

2. 
   Решение:
   

Случайная величина Х задана плотностью распределения f(x):

0, x ≤ 0

A*x, 0 < x < 5

0, x ≥ 5

Найдем параметр A из условия:



Для нашей функции:





или

25*A/2-1 = 0

Откуда, A = 2/25
3)График


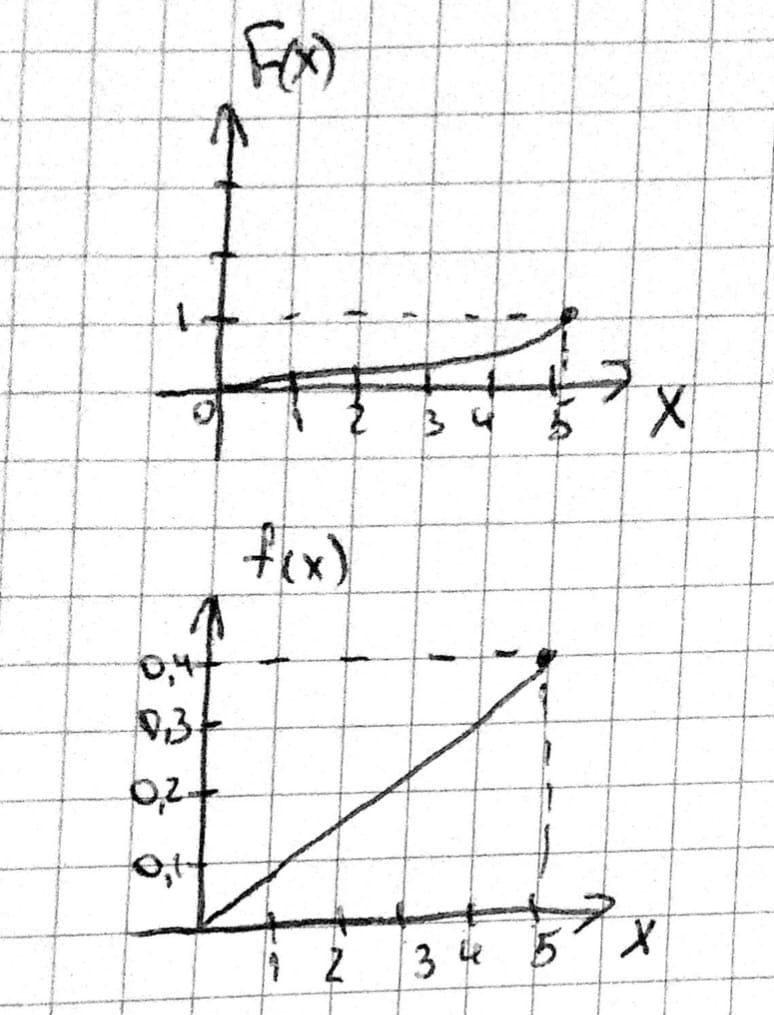
4)Найдем M(X) и D(X) согласно (12) и (14):








5) Вероятность того, что случайная величина Х примет значение из интервала [a,b] равна: P(a < x < b) = F(b) - F(a)


ЗАДАЧА 3

Заданы математическое ожидание aи среднее квадратическое отклонение σ нормально распределенной случайной величины Х.

30.	a = 2, σ = 3, α = 4, β= 8.

---

Требуется:

1. 
   написать функцию плотности распределения вероятностей f(x) и схематично построить ее график;
   
2. 
   найти вероятность того, что Х примет значение из интервала (a, b).
   

1) Функция распределения для нормального распределения задается формулой:

где, erf(x) — функция ошибок (Лапласа) или интеграл вероятности, определяемый как:


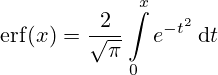
График:

2) Вероятность попадания величины X в заданный интервал (α;β).


ЗАДАЧА 4
Производится некоторый опыт, в котором случайное событие А может появиться с вероятностью p. Опыт повторяют в неизменных условиях n раз.

40. n = 800; p = 0,4 . Определить вероятность того, что в 800 опытах событие А произойдет от 300 до 400 раз.
Исходные данные:p=0.4, q=1-p=1-0.4=0.6
6) событие наступит не менее 300 и не более 400 раз;
Воспользуемся интегральной теоремой Лапласа: P_n(k₁,k₂) = Ф(x₂) – Ф(x₁)
где Ф(x) – функция Лапласа.

k₂ =400,

k₁ =300


Учитывая, что функция Лапласа нечетная, т.е. Ф(-x) = -Ф(x), получим:
P₈₀₀(300 < x < 400) = Ф(5.77) - Ф(1.44) = 0.49999 - (-0.4265) = 0.92649


ЗАДАЧА 5

В результате 10 независимых измерений некоторой величины Х, выполненных

---

с одинаковой точностью, получены опытные данные, приведенные в таблице. Предполагая, что результаты измерений подчинены нормальному закону распределения вероятностей, оценить истинное значение величины Хпри помощи доверительного интервала, покрывающего истинное значение величины Хс доверительной вероятностью 0,95.
_{Исходныеданные}

№ задачи	х1	х2	х3	х4	х5	х6	х7	х8	х9	х10
48.	6,9	7,3	7,1	9,5	9,7	7,9	7,6	9,1	6,6	9,9

Решение:

Поскольку в задаче имеется выборка малого объема, применим распределение Стьюдента.
Фактически требуется построить доверительный интервал для оценки математического ожидания а при неизвестном значении среднеквадратического отклонения из нормально распределенной генеральной совокупности.
Требуется отыскать такое число  , для которого верно равенство

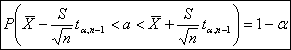
В этой формуле:

- выборочное среднее
S  

---

- стандартное (среднеквадратическое) отклонение
a  - математическое ожидание
n  - объем выборки (нашем случае 10)
 - величина, в сумме с доверительной вероятностью дающая 1 (в нашем случае 0,05)

Величину   (в нашем случае  ) находим по таблицам распределения Стьюдента. Она равна 2,262.
Находим выборочное среднее как среднее арифметическое 

Рассчитаем среднеквадратическое отклонение через исправленную выборочную дисперсию:


Тогда 

Получаем: 

Ответ: истинное значение случайной величины лежит в доверительном интервале (7,257; 9,063) с доверительной вероятностью 0,95.
ЗАДАЧА 6

Отдел технического контроля проверил n партий однотипных изделий и установил, что число Х нестандартных изделий в одной партии имеет эмпирическое распределение, приведенное в таблице, в одной строке которой указано количество x_i нестандартных изделий в одной партии, а в другой строке – количество n_i партий, содержащих x_i нестандартных изделий. Требуется при уровне значимости α = 0,05 проверить гипотезу о том, что случайная величина Х (число нестандартных изделий в одной партии) распределена по закону Пуассона.
_{Исходныеданные}

№ задания	n= ∑ ni	xi	0	1	2	3	4	5
58.	500	ni	194	186	88	26	5	1

---

Смотрите также файлы

• Создание локальной.docx

• Контрольная работа 2 по дисциплине "Английский язык" по теме " Boss private office (What a modern day office should look like).docx

• Э. Дюркгейм об общественной солидарности Воронов А. В.rtf

• 18. Область применения промысловостатистических методов прогноза нефтеотдачи, преимущества и недостатки.pdf

• Подготовка и проведение рабочего совещания. Психологические аспекты.pdf