Решение:Находим выборочную среднюю В качестве оценки параметра l распределения Пуассона   выберем полученное значение выборочного среднего  .Расчет теоретических частот ведем по формуле Расчетная таблица значений. 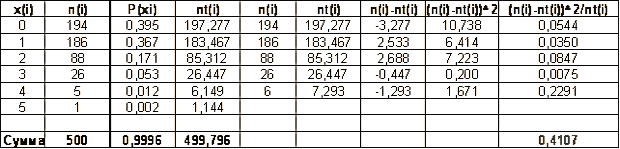Малочисленные частоты   можно объединить. Также объединяются и соответствующие им теоретические частоты.Получили: Число степеней свободы k = s – r – 1, т.к. проверяется гипотеза о распределении Пуассона (т.е. проверяется один параметр), то r = 1,  k = s – 2 = 3 (s = 5, т.к. после исключения малочисленных частот в таблице осталось 5 строк)По таблице получаем: Ответ: поскольку  , гипотеза о том, что случайная величина распределена по закону Пуассона может быть принята. 

---

Смотрите также файлы

• Создание локальной.docx

• Контрольная работа 2 по дисциплине "Английский язык" по теме " Boss private office (What a modern day office should look like).docx

• Э. Дюркгейм об общественной солидарности Воронов А. В.rtf

• 18. Область применения промысловостатистических методов прогноза нефтеотдачи, преимущества и недостатки.pdf

• Подготовка и проведение рабочего совещания. Психологические аспекты.pdf