Файл: Отчет по лабораторной работе 1 Определение коэффициента динамической вязкости жидкости методом Стокса.docx
Добавлен: 24.11.2023
Просмотров: 271
Скачиваний: 15
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и образования Российской Федерации
ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Институт Заочно-вечернего обучения
Отчет по лабораторной работе № 4.1
«Определение коэффициента динамической вязкости жидкости методом Стокса»
Выполнил:
Студент, группы ____/____ (подпись) __/ И. О. Фамилия / (дата)
№ зачетной книжки ________
Принял:
Доцент кафедры физики В. И. Щепин
Иркутск – 2023
Определение коэффициента динамической вязкости жидкости методом Стокса
Цель работы: изучение явления внутреннего трения в жидкостях и опытное определение величины коэффициента вязкости жидкости методом Стокса на виртуальной лабораторной установке.
Теоретическая часть
Различают два типа течения вязкой жидкости – ламинарное и турбулентное. Турбулентным называется такое течение жидкости, при котором её частицы совершают неустановившееся и неупорядоченные движения по сложным траекториям, приводящим к перемешиванию слоёв. Ламинарное – это упорядоченное течение жидкости, при котором траектории движения соседних частиц мало отличаются друг от друга. При ламинарном течении жидкость можно рассматривать как совокупность отдельных слоёв, движущихся с различными скоростями. Это обусловлено тем, что при движении слоев жидкости относительно друг друга с различными скоростями между ними возникает тормозящая сила, это сила внутреннего трения или сила вязкости. Вязкость – это свойство жидкости оказывать противодействие перемещению её слоёв относительно друг друга. Рассмотрим перемещение в жидкости пластинки параллельно плоской стенке.
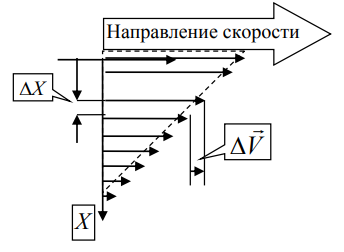
Для перемещения пластинки необходимо приложить силу, по величине равную силе трения. Если слои жидкости находятся на расстоянии Х и движутся с различными скоростями, то верхние слои будут ускорять движение средних слоёв, а нижние – замедлять.
Природа этих сил заключается в том, что слои жидкости, движущиеся с
разными скоростями, обмениваются энергией: слои с молекулами,
имеющими большую скорость, передают некоторое количество движения
более медленным слоям, ускоряя их, но при этом сами подвергаются
торможению. Ньютон показал, что сила внутреннего трения, действующая на
средние слои, прямо пропорциональна градиенту скорости слоев в
направлении, перпендикулярном течению:
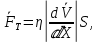
где
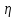 – коэффициент динамической вязкости, равный силе внутреннего
– коэффициент динамической вязкости, равный силе внутреннеготрения, возникающей на единице поверхности соприкосновения слоев,
движущихся относительно друг друга с градиентом скорости, равным
единице. Градиент скорости – это изменение скорости двух слоёв жидкости
dV на расстоянии между слоями dX. Коэффициент динамической вязкости
зависит от природы жидкости и уменьшается с повышением ее температуры.
Закон Ньютона определяет также силу трения, возникающую на границе
между жидкостью и движущимся в ней твердым телом, например шариком.
В системе СИ коэффициент динамической вязкости измеряется в паскаль-секундах.
 паскаль ⸱ секунда → (Па⸱ с) = Н ⸱ с / м²= кг/(м⸱ с);
паскаль ⸱ секунда → (Па⸱ с) = Н ⸱ с / м²= кг/(м⸱ с);До 1980 г. применяли единицу измерения пуаз (П); 1 пуаз = 0,1 Па⸱ с.
Метод Стокса. Стоксом был предложен метод определения
 , основанный на анализе движения шарика, свободно падающего в вязкой жидкости. Это возможно, если плотность материала шарика
, основанный на анализе движения шарика, свободно падающего в вязкой жидкости. Это возможно, если плотность материала шарика 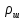 больше плотности жидкости
больше плотности жидкости 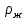 , в которой он движется. Характер движения шарика определяется тремя действующими на него силами: силой тяжести mg, выталкивающей силой Архимеда
, в которой он движется. Характер движения шарика определяется тремя действующими на него силами: силой тяжести mg, выталкивающей силой Архимеда  и силой вязкого трения
и силой вязкого трения 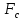 .
. 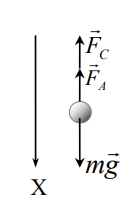
Уравнение движения шарика из основного закона динамики в данном случае принимает вид:
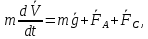 (1)
(1)где т – масса шарика; V – скорость его движения относительно жидкости; g – ускорение свободного падения. В проекции на ось 0х, т.е. на направление
движения шарика, уравнение (1) запишется следующим образом:
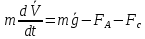
.
Особенность силы вязкого трения заключается в том, что ее величина
зависит от скорости движения тела относительно жидкости. При малых
скоростях эта зависимость прямо пропорциональна. В начале, при
увеличении скорости тела сила трения возрастает настолько, что движение
становится равномерным. Если тело имеет постоянную скорость, т.е.
движение установившееся, то dV/dt = 0; получим уравнение:
mg –
 –
–  = 0. (2)
= 0. (2)Выразим составляющие силы, входящие в уравнение (2), через параметры жидкости и шарика. Для тел сферической формы модуль силы вязкого трения определяется формулой Стокса
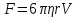 , (3)
, (3)где r – радиус шарика; V – скорость его движения относительно жидкости. Важно отметить, что формула (3) справедлива только в случае ламинарного течения жидкости относительно шарика (скорость движения шарика должна быть небольшой), а жидкость по всем направлениям простирается безгранично, т.е. размеры сосуда, в котором находится жидкость, должны быть много больше по сравнению с размерами шарика. Условия ламинарности можно считать выполненными, если число Рейнольдса Re <
 :
: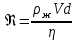 .
.Здесь
 – плотность жидкости, а критическое значение числа Рейнольдса
– плотность жидкости, а критическое значение числа Рейнольдсадля шарика
 , движущегося в жидкости, можно принять равным единицы.
, движущегося в жидкости, можно принять равным единицы.Выразим массу шарика через его плотность и объем:
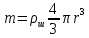 . (4)
. (4)Тогда выражение для архимедовой силы принимает вид:
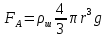 . (5)
. (5)Подставляя выражения (3), (4) и (5) в уравнение (2) и учитывая, что d=2r, после простых преобразований получим:
 . (6)
. (6)Описание экспериментальной установки
Установка для реализации метода Стокса состоит из стеклянного цилиндра (1), в котором находится исследуемая жидкость, вязкость которой необходимо определить.





На цилиндре имеются метки (3 и 4). Расстояние между метками L можно замерить при помощи линейки (6), а диаметр шарика – при помощи микрометра. Время прохождения между метками (3 и 4) можно определить с помощью секундомера (5). Метка (3) помещена на несколько сантиметров ниже верхнего уровня жидкости для выполнения условия равномерного движения шарика в жидкости; V = const на участке L. Цилиндр закрыт пробкой с воронкой, в которую опускается шарик, двигающийся в дальнейшем примерно по оси цилиндра так, чтобы на его движение не влияли стенки.

Вариант №73
Таблица результатов измерений
| № | L, м | 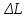 ,м ,м | d, м | 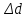 , м , м | t, с | 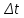 , с , с | V, м/с | Re |  , Па⸱ с , Па⸱ с | 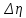 , Па⸱ с , Па⸱ с |
| 1 | 0,45 | 0,005 | 0,006 | 0,00005 | 5,2 | 0,1 | 0,09 | 0,46 | 1,48 | 0,043 |
| 2 | 0,45 | 0,0065 | 4,4 | 0,1 | 0,56 | 1,47 | 0,046 | |||
| 3 | 0,5 | 0,006 | 5,9 | 0,8 | 0,40 | 1,5 | 0,040 | |||
| 4 | 0,5 | 0,0065 | 4,8 | 0,1 | 0,57 | 1,45 | 0,043 | |||
| 5 | 0,47 | 0,0063 | 5,1 | 0,09 | 0,47 | 1,58 | 0,043 |
Таблица относительных погрешностей
| № | L, м |  ,м ,м | d, м |  , м , м | t, с |  , с , с | 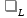 | 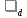 |  | |
| 1 | 0,45 | 0,005 | 0,006 | 0,00005 | 5,2 | 0,1 | 0,011 | 0,0083 | 0,0192 | 0,008 |
| 2 | 0,45 | 0,0065 | 4,4 | 0,011 | 0,0077 | 0,0227 | ||||
| 3 | 0,5 | 0,006 | 5,9 | 0,01 | 0,0083 | 0,0169 | ||||
| 4 | 0,5 | 0,0065 | 4,8 | 0,01 | 0,0077 | 0,0208 | ||||
| 5 | 0,47 | 0,0063 | 5,1 | 0,012 | 0,0079 | 0,0196 |
Абсолютные приборные погрешности прямых измерений:
ΔL = 0,005 м
Δd = 0,00005 м
Δt = 0,1 м
Δ
 = (1,260,01)
= (1,260,01) 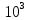 кг/
кг/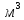
Δ
