Разработка тестовых пакетов

Цель: получить навыки разработки тестовых пакетов.

Теоретические сведения:

В ходе выполнения лабораторной работы провести тестирование по принципу «белого ящика».

Критерии покрытия кода:

• 
  покрытие операторов — каждая ли строка исходного кода была выполнена и протестирована;
  
• 
  покрытие условий — каждая ли точка решения (вычисления истинно ли или ложно выражение) была выполнена и протестирована;
  
• 
  покрытие путей — все ли возможные пути через заданную часть кода были выполнены и протестированы;
  
• 
  покрытие функций — каждая ли функция программы была выполнена;
  
• 
  покрытие вход/выход — все ли вызовы функций и возвраты из них были выполнены;
  
• 
  покрытие значений параметров — все ли типовые и граничные значения параметров были проверены.
  

Метод покрытия операторов

Целью этого метода тестирования является выполнение каждого оператора программы хотя бы один раз.

Пример.

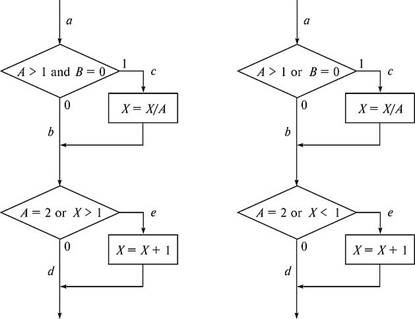
Если для тестирования задать значения переменных А = 2, В= О, Х=3, будет реализован путь асе, т. е. каждый оператор программы выполнится один раз (рис. Л5.1, а). Но если внести в алгоритм ошибки — заменить в первом условии and на or, а во втором Х> 1 на Х< 1 (рис. Л5.1, б), ни одна ошибка не будет обнаружена (табл. Л5.1). Кроме того, путь abd вообще не будет охвачен тестом, и если в нем есть ошибка, она также не будет обнаружена. В табл. Л5.1 ожидаемый результат определяется по блок-схеме на рис. Л5.1, а, а фактический — по рис. Л5.1, б.

Как видно из этой таблицы, ни одна из внесенных в алгоритм ошибок не будет обнаружена.

Таблица Л5.1. Результат тестирования методом покрытия операторов





а) б)

Рис. Л5.1. Пример алгоритма программы: а — правильный; б — с ошибкой

Метод покрытия решений (покрытия переходов)

Согласно методу покрытия решений, каждое направление перехода должно быть реализовано, по крайней мере, один раз. Этот метод включает в себя критерий покрытия операторов, так как при выполнении всех направлений переходов выполнятся все операторы, находящиеся на этих направлениях.

---

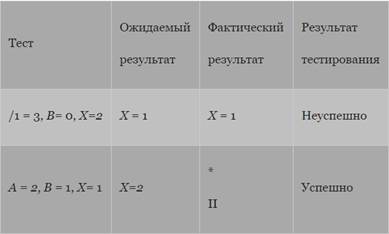
Для программы, приведенной на рис. Л5.1, покрытие решений может быть выполнено двумя тестами, покрывающими пути {асе, аЬс!}, либо {асс1, аЬе}. Для этого выберем следующие исходные данные; {А = 3, В= О, Х=3} — в первом случае и {А = 2, В= 1, Х= 1} — во втором. Однако путь, где X не меняется, будет проверен с вероятностью 50 %: если во втором условии вместо условия Х> 1 записано Х<, то ошибка не будет обнаружена двумя тестами.

Результаты тестирования приведены в табл. Л5.2.

Таблица Л5.2. Результат тестирования методом покрытия решений



Метод покрытия условий

Этот метод может дать лучшие результаты по сравнению с предыдущими. В соответствии с методом покрытия условий записывается число тестов, достаточное для того, чтобы все возможные результаты каждого условия в решении выполнялись, по крайней мере, один раз.

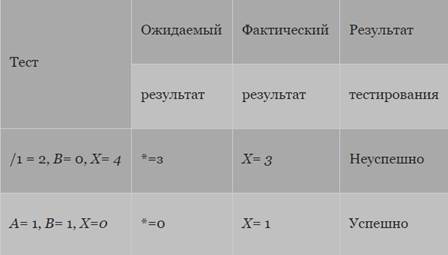
В рассматриваемом примере имеем четыре условия: {А> 1, 5=0}, {А = 2, Х> 1}. Следовательно, требуется достаточное число тестов, такое, чтобы реализовать ситуации, где А > 1, А < 1, 5 = 0 и й#0 в точке а и /1 = 2, А *2, Х> и Т< 1 в точке Ь. Тесты, удовлетворяющие критерию покрытия условий (табл. Л5.3), и соответствующие им пути:

· а) А = 2, 5 = 0, Х=4 асе;

· б) А = 1, 5= 1, Х=0 аbс!.

Таблица Л5.3. Результаты тестирования методом покрытия условий



Метод покрытия решений/условий

Критерий покрытия решений/условий требует такого достаточного набора тестов, чтобы все возможные результаты каждого условия выполнялись по крайней мере один раз, все результаты каждого решения выполнялись по крайней мере один раз и, кроме того, каждой точке входа передавалось управление по крайней мере один раз.

Недостатки метода:

• 
  • не всегда можно проверить все условия;
  
• 
  • невозможно проверить условия, которые скрыты другими условиями;
  
• 
  • недостаточная чувствительность к ошибкам в логических выражениях.
  

Так, в рассматриваемом примере два теста метода покрытия условий

---

а) А = 2, В = О, Х= 4 асе;

б) А= 1, В= 1, Х=0 аbс!

отвечают и критерию покрытия решений/условий. Это является следствием того, что одни условия приведенных решении скрывают другие условия в этих решениях. Так, если условие А > 1 будет ложным, транслятор может не проверять условия В= О, поскольку при любом результате условия В= 0 результат решения ((А > )&(В=0)) примет значение ложь. То есть в варианте на рис. Л5.1 не все результаты всех условий выполнятся в процессе тестирования.

Рассмотрим реализацию того же примера на рис. Л5.2. Наиболее полное покрытие тестами в этом случае осуществляется



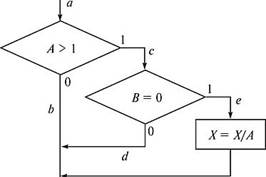
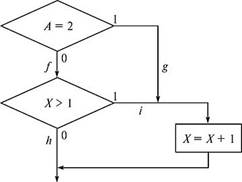
так, чтобы выполнялись все возможные результаты каждого простого решения. Для этого нужно покрыть пути aceg (тест А = 2, В= О, Х= 4), асё/к (тест А = 3, В = 1, Х= 0), аЬ/к (тест А = 0, В= 0, Х= 0), аЬр (тест Л = 0, В = 0, Х= 2).

Протестировав алгоритм на рис. Л5.2, нетрудно убедиться в том, что критерии покрытия условий и критерии покрытия решений/условий недостаточно чувствительны к ошибкам в логических выражениях.

Метод комбинаторного покрытия условий

Критерий комбинаторного покрытия условий удовлетворяет также и критериям покрытия решений, покрытия условий и покрытия решений/условий.

Этот метод требует создания такого числа тестов, чтобы все возможные комбинации результатов условия в каждом решении выполнялись по крайней мере один раз. По этому критерию в рассматриваемом примере должны быть покрыты тестами следующие восемь комбинаций:

• 
  1. А> 1, В= 0. 5. А = 2, Х> 1.
  
• 
  2. А > 1, Вф 0.
  
• 
  3. А< 1, В= 0.
  
• 
  4. А< 1, Вф 0.
  
• 
  6. А = 2, 1.
  
• 
  7. Аф2, Х> 1.
  
• 
  8. Аф2, Х< 1.
  

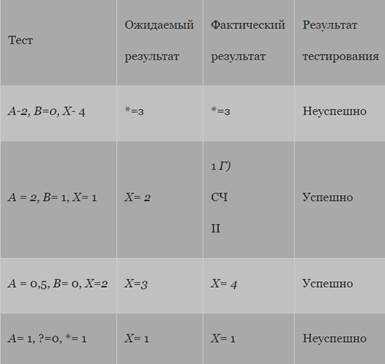
Для того чтобы протестировать эти комбинации, необязательно использовать все 8 тестов. Фактически они могут быть покрыты четырьмя тестами (табл. Л5.4):

• 
  • А = 2, В = 0, Х=4 (покрывает 1,5};
  
• 
  • А = 2, В = 1, Х= 1 (покрывает 2,6};
  
• 
  • А = 0,5, В= 0, Х= 2 (покрывает 3, 7};
  
• 
  • А = I, В = 0, Х= (покрывает 4, 8}.
  

Таблица Л5.4. Результаты тестирования методом комбинаторного покрытия условий

---

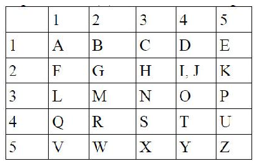
Задание № 1. В Древней Греции (II в. до н.э.) был известен шифр, называемый "квадрат Полибия". Шифровальная таблица представляла собой квадрат с пятью столбцами и пятью строками, которые нумеровались цифрами от 1 до 5. В каждую клетку такого квадрата записывалась одна буква. В результате каждой букве соответствовала пара чисел, и шифрование сводилось к замене буквы парой чисел. Для латинского алфавита квадрат Полибия имеет вид:



Пользуясь вышеизложенным способом написать программу, которая:

а) зашифрует введенный текст и выведет на экран;

б) считает зашифрованный текст и расшифрует данный текст (пункт б выполнить по желанию и возможностям).

Задание № 2. Выбрать один из методов. Спроектировать тесты по принципу «белого ящика» для программы,разработанной в задании № 1. Выбрать алгоритм для тестирования, обозначить буквами или цифрами ветви этих алгоритмов. Выписать пути алгоритма, которые должны быть проверены тестами для выбранного метода тестирования. Записать тесты, которые позволят пройти по путям алгоритма. Протестировать разработанную вами программу. Результаты оформить в виде таблицы:



Задание № 3. Проверить все виды тестов и сделать выводы об их эффективности.

Задание № 4. Оформить отчет.

---

Смотрите также файлы

• Отчет по индивидуальной работе 1 Производная и дифференциал. Приложения производной.docx

• 1. Вершины сетевой модели типа Работа Дуга отображают .pdf

• Автономная некоммерческая организация высшего образования московский международный университет совместный рабочий график (план) проведения с 27. 06. 2022 24. 07. 2022.docx

• Методические указания по выполнению курсовой работы по дисциплине Теоретические основы электротехники для обучающихся направления подготовки.pdf

• Программа Открой себя Программа Открой себя.pptx