Файл: Курсовой проект состоит из пяти листов графического материала, а также пояснительной записки.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 43
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
неизвестна по направлению.
Реакцию раскладываем на 2 взаимно перпендикулярные составляющие:
раскладываем на 2 взаимно перпендикулярные составляющие: 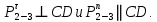
Запишем уравнение моментов всех сил, действующих на звено 3, относительно точки :
:
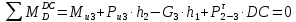 , отсюда
, отсюда
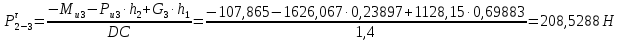
Далее, приняв масштаб сил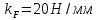 , строим план сил по векторному уравнению:
, строим план сил по векторному уравнению:
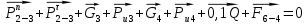
Из плана сил находим величины и направления сил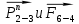 , а также полную реакцию в паре с
, а также полную реакцию в паре с 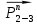 (
(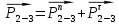 ).
).
Переходим к силовому расчету группы Ассура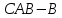 . Освобождаем от связей и прикладываем реакции
. Освобождаем от связей и прикладываем реакции 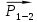 и
и 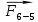 , которые неизвестны ни по величине, ни по направлению.
, которые неизвестны ни по величине, ни по направлению.
Реакцию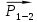 раскладываем на 2 взаимно перпендикулярные составляющие:
раскладываем на 2 взаимно перпендикулярные составляющие: 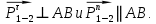
Запишем уравнение моментов всех сил, действующих на звено 2, относительно точки :
:
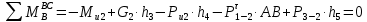 , отсюда
, отсюда
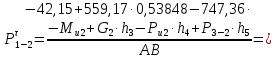
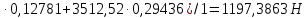
Задавшись масштабом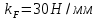 , строим план сил по векторному уравнению:
, строим план сил по векторному уравнению:
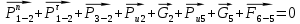
Из плана сил находим величины и направления сил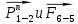 , а также полную реакцию в паре
, а также полную реакцию в паре  : (
: (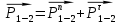
).
4.3. Силовой расчет входного звена механизма
Для определения реакции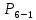 в кинематической паре, образованной входным звеном и стойкой, необходимо привести в равновесие все силы, действующие на это звено с учетом уравновешивающей силы. Уравновешивающая сила является реальной внешней силой, которая представляет собой действие привода на звено
в кинематической паре, образованной входным звеном и стойкой, необходимо привести в равновесие все силы, действующие на это звено с учетом уравновешивающей силы. Уравновешивающая сила является реальной внешней силой, которая представляет собой действие привода на звено  .
.
Величину уравновешивающей силы находим из уравнения моментов относительно точки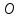 всех сил, действующих на звено 1:
всех сил, действующих на звено 1:
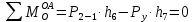 , отсюда
, отсюда
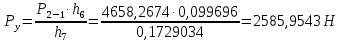
Для определения численного значения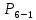 строим план сил в масштабе
строим план сил в масштабе 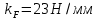 согласно векторному уравнению:
согласно векторному уравнению:
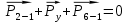
Результаты силового расчёта с использованием планов сил указаны в табл. 4.1.
Табл. 4.1. Реакции в кинематических парах рычажного механизма для положения 4, Н
4.4. Определение уравновешивающей силы методом Н.Е. Жуковского
Чтобы найти уравновешивающую силу методом Н.Е. Жуковского построим план скоростей и в соответствующие точки этого плана перенесём все силы (внешние и инерции), действующие на звенья механизма, предварительно повернув их в одном направлении на угол
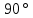 .
.
Моменты сил инерции заменяем парами сил:
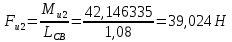
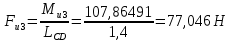
Рассматривая план скоростей как жёсткий рычаг, который находится в равновесии, определим сумму моментов всех сил относительно полюса:
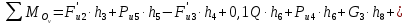
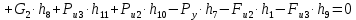
Выражаем из этого уравнения :
:
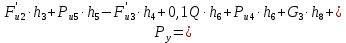
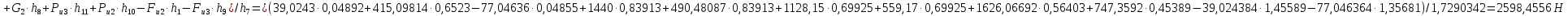
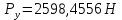
Погрешность в расчётах уравновешивающей силы разными способами составляет:
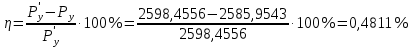
5. Динамический расчет механизма
Внутри цикла установившегося движения угловая скорость начального звена машины периодически меняется из-за постоянного изменения нагрузок, что приводит к нежелательной неравномерности движения. Неравномерность движения начального звена характеризуется коэффициентом неравномерности движения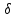 , который не должен превышать допускаемого значения
, который не должен превышать допускаемого значения 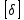 . Для снижения колебаний угловой скорости начального звена до допустимых пределов в машине предусматривают маховик, который с целью уменьшения его размеров устанавливают на быстроходном валу. Задачей динамического расчета механизма является определение расхода мощности и основных геометрических размеров маховика по заданному коэффициенту
. Для снижения колебаний угловой скорости начального звена до допустимых пределов в машине предусматривают маховик, который с целью уменьшения его размеров устанавливают на быстроходном валу. Задачей динамического расчета механизма является определение расхода мощности и основных геометрических размеров маховика по заданному коэффициенту 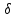 неравномерности хода машины.
неравномерности хода машины.
5.1. Приведение сил, построение диаграммы работ и их разностей
С использованием диаграммы силы сопротивления, действующей на ползун , изображаем на соответствующем листе проекта график характеристики технологической силы от положения механизма. Определяем численные значения силы сопротивления по формуле
, изображаем на соответствующем листе проекта график характеристики технологической силы от положения механизма. Определяем численные значения силы сопротивления по формуле
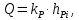
где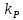 – масштаб диаграммы сил;
– масштаб диаграммы сил; 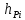 – ордината диаграммы для данного положения механизма.
– ордината диаграммы для данного положения механизма.
Численные значения силы сопротивления указываем в табл. 5.1.
Приведение сил для -го положения механизма по методу Жуковского осуществляется по формуле:
-го положения механизма по методу Жуковского осуществляется по формуле:
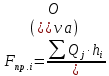
Здесь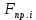 – приведенная сила;
– приведенная сила; 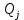 – активная сила, приложенная к звену
– активная сила, приложенная к звену 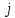 ;
;
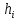 - плечо этой силы в плане скоростей относительно его полюса;
- плечо этой силы в плане скоростей относительно его полюса;
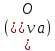 – графическое изображение скорости точки приведения (пальца кривошипа) на плане скоростей.
– графическое изображение скорости точки приведения (пальца кривошипа) на плане скоростей.
Табл. 5.1. Внешняя сила, действующая на ползун
Момент приведенной силы, или приведенный момент
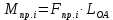
где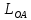 – удаление точки приведения от оси вращения начального звена (длина кривошипа).
– удаление точки приведения от оси вращения начального звена (длина кривошипа).
Для седьмого положения механизма:
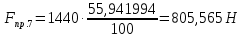
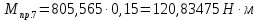
Поскольку цикл машины соответствует одному обороту ведущего звена, то приведенные силы и их моменты отыскиваем для двенадцати положений механизма. В соответствии с результатами расчета на чертежном листе строим диаграмму приведенных моментов в функции угла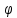 поворота кривошипа.
поворота кривошипа.
Численные значения приведённых сил и приведённых моментов сил сопротивления указаны в табл. 5.2.
В седьмом положении механизма приведенный момент изобразим на диаграмме «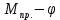 » отрезком
» отрезком 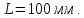 Масштаб приведенных моментов на диаграмме «
Масштаб приведенных моментов на диаграмме «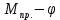 »
»
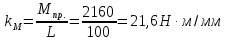
Масштаб угла поворота начального звена (кривошипа)
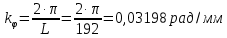
Путем графического интегрирования диаграммы приведенных моментов строим диаграмму работ заданных сил сопротивления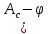 ) за цикл. На этом же графике строится диаграмма работ движущихся сил. При этом предполагается, что приведенный движущийся момент есть величина постоянная. Следовательно, работа этого момента будет выражаться прямолинейной зависимостью в системе координат «
) за цикл. На этом же графике строится диаграмма работ движущихся сил. При этом предполагается, что приведенный движущийся момент есть величина постоянная. Следовательно, работа этого момента будет выражаться прямолинейной зависимостью в системе координат «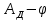 ».
».
Таблица 5.2. Приведение силы и их моменты сил сопротивления
Реакцию
 раскладываем на 2 взаимно перпендикулярные составляющие:
раскладываем на 2 взаимно перпендикулярные составляющие: 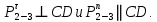
Запишем уравнение моментов всех сил, действующих на звено 3, относительно точки
 :
: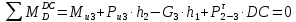 , отсюда
, отсюда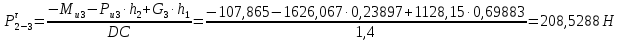
Далее, приняв масштаб сил
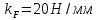 , строим план сил по векторному уравнению:
, строим план сил по векторному уравнению: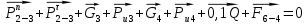
Из плана сил находим величины и направления сил
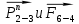 , а также полную реакцию в паре с
, а также полную реакцию в паре с 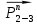 (
(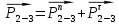 ).
).Переходим к силовому расчету группы Ассура
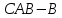 . Освобождаем от связей и прикладываем реакции
. Освобождаем от связей и прикладываем реакции 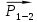 и
и 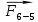 , которые неизвестны ни по величине, ни по направлению.
, которые неизвестны ни по величине, ни по направлению.Реакцию
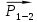 раскладываем на 2 взаимно перпендикулярные составляющие:
раскладываем на 2 взаимно перпендикулярные составляющие: 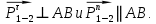
Запишем уравнение моментов всех сил, действующих на звено 2, относительно точки
 :
: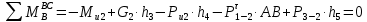 , отсюда
, отсюда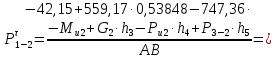
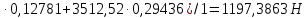
Задавшись масштабом
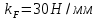 , строим план сил по векторному уравнению:
, строим план сил по векторному уравнению: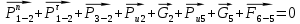
Из плана сил находим величины и направления сил
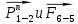 , а также полную реакцию в паре
, а также полную реакцию в паре  : (
: (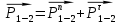
).
4.3. Силовой расчет входного звена механизма
Для определения реакции
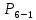 в кинематической паре, образованной входным звеном и стойкой, необходимо привести в равновесие все силы, действующие на это звено с учетом уравновешивающей силы. Уравновешивающая сила является реальной внешней силой, которая представляет собой действие привода на звено
в кинематической паре, образованной входным звеном и стойкой, необходимо привести в равновесие все силы, действующие на это звено с учетом уравновешивающей силы. Уравновешивающая сила является реальной внешней силой, которая представляет собой действие привода на звено  .
.Величину уравновешивающей силы находим из уравнения моментов относительно точки
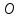 всех сил, действующих на звено 1:
всех сил, действующих на звено 1: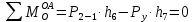 , отсюда
, отсюда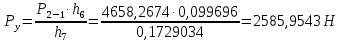
Для определения численного значения
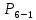 строим план сил в масштабе
строим план сил в масштабе 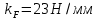 согласно векторному уравнению:
согласно векторному уравнению: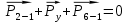
Результаты силового расчёта с использованием планов сил указаны в табл. 4.1.
Табл. 4.1. Реакции в кинематических парах рычажного механизма для положения 4, Н
 |  | 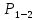 | 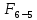 | 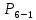 | 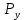 |
| 594,60118 | 3512,5216 | 4658,2674 | 515,4144 | 6565,876 | 2585,9543 |
4.4. Определение уравновешивающей силы методом Н.Е. Жуковского
Чтобы найти уравновешивающую силу методом Н.Е. Жуковского построим план скоростей и в соответствующие точки этого плана перенесём все силы (внешние и инерции), действующие на звенья механизма, предварительно повернув их в одном направлении на угол
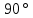 .
.Моменты сил инерции заменяем парами сил:
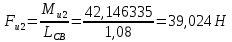
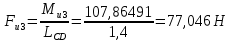
Рассматривая план скоростей как жёсткий рычаг, который находится в равновесии, определим сумму моментов всех сил относительно полюса:
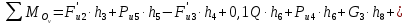
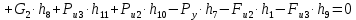
Выражаем из этого уравнения
 :
: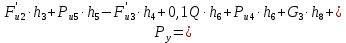
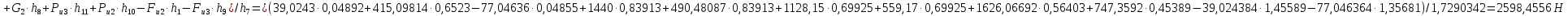
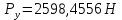
Погрешность в расчётах уравновешивающей силы разными способами составляет:
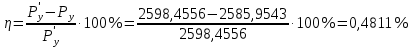
5. Динамический расчет механизма
Внутри цикла установившегося движения угловая скорость начального звена машины периодически меняется из-за постоянного изменения нагрузок, что приводит к нежелательной неравномерности движения. Неравномерность движения начального звена характеризуется коэффициентом неравномерности движения
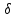 , который не должен превышать допускаемого значения
, который не должен превышать допускаемого значения 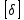 . Для снижения колебаний угловой скорости начального звена до допустимых пределов в машине предусматривают маховик, который с целью уменьшения его размеров устанавливают на быстроходном валу. Задачей динамического расчета механизма является определение расхода мощности и основных геометрических размеров маховика по заданному коэффициенту
. Для снижения колебаний угловой скорости начального звена до допустимых пределов в машине предусматривают маховик, который с целью уменьшения его размеров устанавливают на быстроходном валу. Задачей динамического расчета механизма является определение расхода мощности и основных геометрических размеров маховика по заданному коэффициенту 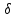 неравномерности хода машины.
неравномерности хода машины. 5.1. Приведение сил, построение диаграммы работ и их разностей
С использованием диаграммы силы сопротивления, действующей на ползун
 , изображаем на соответствующем листе проекта график характеристики технологической силы от положения механизма. Определяем численные значения силы сопротивления по формуле
, изображаем на соответствующем листе проекта график характеристики технологической силы от положения механизма. Определяем численные значения силы сопротивления по формуле
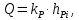
где
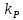 – масштаб диаграммы сил;
– масштаб диаграммы сил; 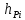 – ордината диаграммы для данного положения механизма.
– ордината диаграммы для данного положения механизма.Численные значения силы сопротивления указываем в табл. 5.1.
Приведение сил для
 -го положения механизма по методу Жуковского осуществляется по формуле:
-го положения механизма по методу Жуковского осуществляется по формуле: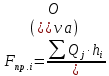
Здесь
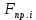 – приведенная сила;
– приведенная сила; 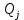 – активная сила, приложенная к звену
– активная сила, приложенная к звену 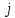 ;
;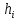 - плечо этой силы в плане скоростей относительно его полюса;
- плечо этой силы в плане скоростей относительно его полюса;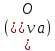 – графическое изображение скорости точки приведения (пальца кривошипа) на плане скоростей.
– графическое изображение скорости точки приведения (пальца кривошипа) на плане скоростей. Табл. 5.1. Внешняя сила, действующая на ползун

| Сила | Положение механизма | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
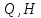 | 4382,609 | 4382,609 | 14400 | 14400 | 14400 | 4382,609 | 1440 | 1440 | 1440 | 1440 | 1440 | 1440 |
Момент приведенной силы, или приведенный момент
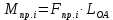
где
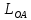 – удаление точки приведения от оси вращения начального звена (длина кривошипа).
– удаление точки приведения от оси вращения начального звена (длина кривошипа).Для седьмого положения механизма:
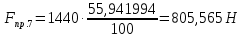
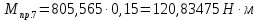
Поскольку цикл машины соответствует одному обороту ведущего звена, то приведенные силы и их моменты отыскиваем для двенадцати положений механизма. В соответствии с результатами расчета на чертежном листе строим диаграмму приведенных моментов в функции угла
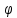 поворота кривошипа.
поворота кривошипа.Численные значения приведённых сил и приведённых моментов сил сопротивления указаны в табл. 5.2.
В седьмом положении механизма приведенный момент изобразим на диаграмме «
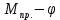 » отрезком
» отрезком 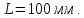 Масштаб приведенных моментов на диаграмме «
Масштаб приведенных моментов на диаграмме «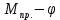 »
»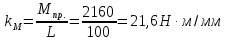
Масштаб угла поворота начального звена (кривошипа)
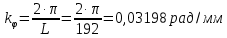
Путем графического интегрирования диаграммы приведенных моментов строим диаграмму работ заданных сил сопротивления
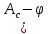 ) за цикл. На этом же графике строится диаграмма работ движущихся сил. При этом предполагается, что приведенный движущийся момент есть величина постоянная. Следовательно, работа этого момента будет выражаться прямолинейной зависимостью в системе координат «
) за цикл. На этом же графике строится диаграмма работ движущихся сил. При этом предполагается, что приведенный движущийся момент есть величина постоянная. Следовательно, работа этого момента будет выражаться прямолинейной зависимостью в системе координат «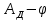 ».
». Таблица 5.2. Приведение силы и их моменты сил сопротивления
| Приведенная сила, момент | Положение механизма | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
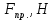 | 0 | 1930,8898 | 11610,231 | 14400 | 13395,685 | 2451,7186 | 0 | 805,565 | 1332,9514 | 1440 | 1161,2017 | 634,4352 |
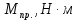 | 0 | 289,6335 | 1741,535 | 2160 | 2009,353 | 367,7578 | 0 | 120,8348 | 199,9427 | 216 | 174,1803 | 95,1653 |