МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ __________________________________________________________________Федеральное государственное бюджетное образовательное учреждение высшего образования «Пензенский государственный университет архитектуры и строительства» Кафедра «Водоснабжение, водоотведение и гидротехника»Расчетно-графическая работапo дисциплине «Механика жидкости и газа» Выпoлнил: студент 2 курса группы 21СТ2з Придиус Д.АПрoвeрил: д.т.н. профессорГришин Б.М.РАСЧЕТ СБРОСНОГО ТРУБОПРОВОДА ИЗ БАКА С ПОСТОЯННЫМ УРОВНЕМ ВОДЫ. Из бака при постоянном напоре Н по прямому горизонтальному трубопроводу состоящему из трех участков различной длины, но одного диаметра вытекает вода в атмосферу. На расстоянии l₁ от начала трубопровода установлена задвижка степенью закрытия , На расстоянии l₂ от задвижки устанавливается диафрагма Определить расход воды в трубопроводе и построить пьезометрическую и напорную линии, если: заданы диаметры и длины участков труб; напор Н+Н₁= 11,2+3,4=14,6 м; трубы чугунные новые с покрытием. Плотность воды ρ=1000 кг/м3, кинематический коэффициент вязкости ν=10^-6 м2/с._{В масштабе построить линии полного и пьезометрического напора}

Найти Q - ?

Плотность воды , кинематическая вязкость Абсолютная шероховатость трубы чугунной новый с покрытием

---

(0,45мм)

Составляем уравнение Бернулли для сечении 1-1 проходящий по поверхности воды в емкости и сечении 4-4 по сечению трубы на выходе Плоскость сравнения (0-0) по сечению 4-4



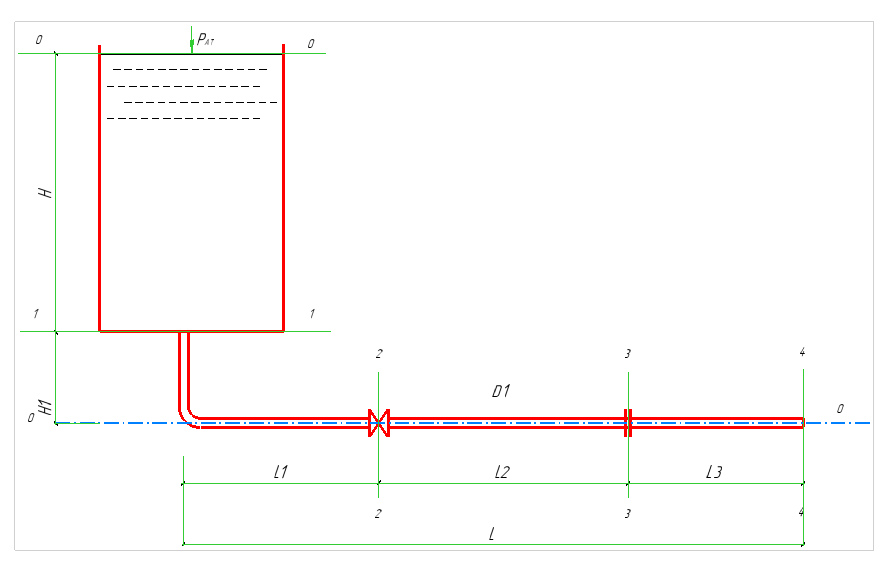
Рис.1

Решение. Составим уравнение Бернулли для сечений 0—0 и 4—4 относительно плоскости сравнения 0' — 0', проведенной через ось трубы

z₀ + (P₀)/ρg+(αυ₀²)/2g=z₄ + (P₄)/ρg+(αυ₄²)/2g+h_n0-4 (1)

В рассматриваемом случае z₀ = Н, р₀ = р₄ = p_ат, z₄ = 0. Поскольку скорость движения воды в баке несоизмеримо меньше скорости движения воды в трубе, можно принять, что υ₀≈ 0.

Тогда h_n0-4 = Σh_m +h_дл1 = Σ υ₄²/2gξ_m+λl₁υ₄²/D₁2g (2)

Где h_дл1-потери напора по длине на первом участке;

h_м –местные потери, которые равны:

h_м =ξυ²/2g (3)

α=1,1 коэффициент Кориолиса – исходя из предположения о турбулентном потоке воды в трубе

так как расчет ведем для избыточного давления



- так как уровень воды в емкости не меняется,

Составим уравнение Бернулли для сечений 0-0 и 4-4

z₁ + (P₁)/ρg+(αυ₁²)/2g=z₂ + (P₄)/ρg+(αυ₄²)/2g+h_1-4,

где h_1-2 –потери напора между сечениями.

В данном случае сумма коэффициентов потерь Σζ_м местных сопротивлений складывается из коэффициента на входе в трубу ζ_вх =0,5, ξпов 0,45– потери при плавном повороте: ξзадв 2,568– потери напора на кране, h_диаф 4 – потери диафрагмы; где ω

ω=0,012м

Σζ_{м =} ζ_вх + ξпов+ ξзадв+ h_диаф

Σζ_{м = 7,518}

Так как область гидравлического сопротивления в трубопроводе неизвестна, то в первом приближении принимаем, что имеет место квадратичный закон сопротивления.

Принимаем в первом приближении, что потоки в трубе турбулентные, в области квадратичного трения , тогда коэффициент гидравлического трения рассчитываются по формуле

---

λ=0,11(Δ_э/D)^0,25 (4)где Δ_э =0,45– эквивалентная шероховатость стальной чугунной новый с покрытием.Коэффициент гидравлического трения определяем по формуле λ=0,11(Δ_э/D₁)^0,25=0,11(0,45/0,2)^0,25=0,024;Где ∆э=0,45 мм – эквивалентная шероховатость чугунные трубы новые с покрытиемПодставляя известные величины в формулу для расхода.Q=πD2/4∙√2gH/ α +Σξм+λ l/D, находим для участка L :Q=3,14∙0,2²/4∙√2∙9,81∙11,2/1,1+7,518+0,024*109,4/0,2=0,1166м3/сУточним режим движения жидкостиНаходим число Рейнольдса для трубопровода на участке L:Re=4 Q₁/πD₁ν=4∙0,1166 /3,14∙0,2∙10^-6=7,4267∙10⁵;Так как Re >500D₁/Δ_э=500∙200/0.45=2,22∙10⁵,то область сопротивления квадратичная и коэффициент λ₁ определен правильно. Для нахождения потерь напора по длине, вычислим υ по формуле: υ=Q/ω (5)для участка L:υ=Q/ω=0,1/0,0314=3,712 м/сПостроение графика Бернулли выполним в следующейпоследовательности.Проводим плоскость сравнения О-О и на ней отмечаем характерныеточки: 0, 1 – вход в трубу l1; 2 – задвижка; 3 – диафрагма; 4 – выход из трубы. Через эти точки проводим вспомогательные вертикальные линии.Точка О' соответствует значению полного (начального) напора передвходом в трубуН=14,6 мПосле входа в трубу (точка 1) произойдет потеря на входНаходим потери по длине для участка L.h_вх = ξ_вх∙υ²/2g=0,5∙3,712²/2∙9,81=0,3511м;Потери по длине на участке 1-2h_1-2= λ∙ l₁/d∙υ²/2∙ g= 0,024∙18/0,2∙3,712²/2∙9,81=1,5160м;Затем потери на задвижке:h _задв = ξ_задв ∙ υ²/2∙ g = 2,568∙3,712²/2∙9,81= 1,8025м;Потери по длине на участке 2-3:h l_2-3= λ∙ l₂/d∙υ²/2∙ g=0,024∙43/0,2∙3,712²/2∙9,81=3,6392м;Потери диафрагмы:hдиафр = ξ_диафр ∙ υ²/2∙g = 4∙3,712²/2∙9,81=2,8090м;Потери по длине на участке 3-4:hl_3-4= λ∙ l₃/d∙υ²/2∙ g=0,024∙45/0,2∙3,712²/2∙9,81=3,68;Суммарные потери напора при движении жидкости по трубопроводусоставят:h=+Σ hL+ Σ hм=0,3511+1,5160+1,8025+3,6392+2,8092+3,68=13,7978мЛиния О'-1'-2'-3'-4' будет линией полного напора реальной жидкости,вязкость и плотность которой заданы значениями ν и ρДля построения пьезометрической линии необходимо отложить вниз от линии полного напора в соответствующих точках значения скоростных

---

напоров h_v= 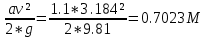.Линия 1''-2''-3''-4'' – пьезометрическая линия.Потери напора при движении потока по трубе показаны заштрихованной областьюОтвет: .

---

Смотрите также файлы

• Финансы предприятий и организаций.docx

• Петр Великий личностный аспект.docx

• Курсовой проект по дисциплине Технология бетона и железобетона Ташкент 2017 Оглавление.docx

• Влияние цитопротектора ребамипида на активность дисахаридаз у больных энтеропатией с нарушением мембранного пищеварения..docx

• Курсовая работа по дисциплине Методы и средства проектирования информационных систем и технологий на тему Разработка регламента выполнения процесса Движение библиотечного фонда.docx