Файл: 1. Областью определения функции является множество а) (1 1) б) (0 1) в) (10 10) г) ( 1).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 11
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1. Областью определения функции
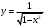 является множество
является множествоа) (-1; 1) +; б) (0; 1); в) (-10; 10); г) (-∞; 1).
2. Областью определения функции
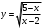 является множество
является множествоа) (2; 5] +; б) (2; 5); в) [2; 5]; г) (-; 2) (5; +).
3. Областью значения функции
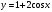 является множество
является множествоа) (-1; 1); б) (-2; 2); в) (-1; 3) +; г) (-∞; 1).
4. Дана функция
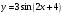 . Тогда ее областью значений является множество
. Тогда ее областью значений является множествоа) [-1; 1]; б) [-3; 3] +; в) [-6; 6]; г) (-∞;+∞).
5. Значение предела
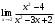 равно…
равно…а) 4 +; б) 1; в) -3; г) – 4.
6. Значение предела
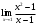 равно…
равно…а) 2 +; б) ∞; в) 1; г) 0.
7. Значение предела
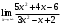 равно…
равно…а) 3/5; б) 5/3 +; в) 1; г) 0.
8. Значение предела
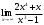 равно…
равно…а) 2; б) ∞ +; в) -1; г) 0.
9. Производная функции
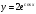 равна
равнаа)
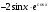 +; б)
+; б) 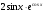 ; в)
; в) 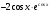 ; г)
; г) 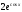 .
.10. Производная функции
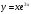 равна
равнаа)
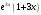 +; б)
+; б) 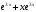 ; в)
; в) 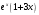 ; г)
; г) 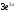 .
.11. Найти производную
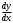 , если функция задана параметрически
, если функция задана параметрически 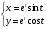 при t = /2
при t = /2a) 0; б) 1; в) 2; г) -1 +.
12. Найти производную
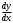 , если функция задана параметрически
, если функция задана параметрически 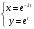 при t = 1
при t = 1a) -e3; б) 1/e3; в) -2/e3; г) -e3/2 +.
13. Найти частную производную
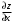 , если
, если 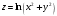
а)
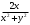 +; б)
+; б) 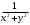 ; в)
; в) 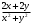 ; г)
; г) 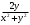 .
.14. Найти частную производную
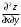 , если
, если 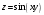
а)
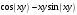 +; б)
+; б) 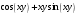 ; в)
; в) 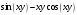 ; г)
; г) 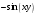 .
.15. Чему равен неопределенный интеграл
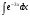
а)
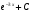 ; б)
; б) 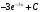 ; в)
; в) 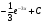 +; г)
+; г) 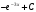 .
.16. Чему равен неопределенный интеграл
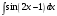
а)
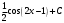 ; б)
; б) 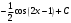 +; в)
+; в) 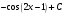 ; г)
; г) 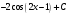 .
.17. Определенный интеграл
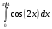 равен
равена) 0; б) 0,5 +; в) 1; г) 2.
18. Определенный интеграл
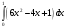 равен
равена) 0; б) -1; в) 1 +; г) 8.
19. Вычислить интеграл
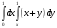
а) 0; б) 1/2 +; в -1/2; г) -1; д) 1.
20. Вычислить интеграл
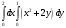
а) 14/3 +; б) 6; в) 20/3; г) -1.
21. Если на отрезке [a, b] функция f(x) имеет положительную производную
 , то
, тоа) f(x) – убывает; б) f(x) – возрастает +; в) f(x) – выпукла вверх; г) f(x) – выпукла вниз.
22. На рисунке изображен график функции y = f(x), заданной на интервале (-3; 6). Тогда число интервалов на которых производная функции отрицательна f`(x) < 0, равно
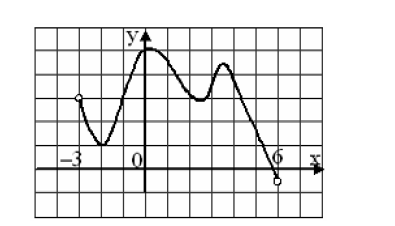
а) 4; б) 1; в) 2; г) 3 +.
23. Если на отрезке [a, b] функция f(x) имеет положительную производную 2-го порядка
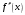 , то
, тоа) f(x) – убывает; б) f(x) – возрастает; в) f(x) – выпукла вверх; г) f(x) – выпукла вниз +.
24. На рисунке изображен график функции y = f(x), заданной на интервале (1; 6). Тогда на этом интервале выполняются неравенства
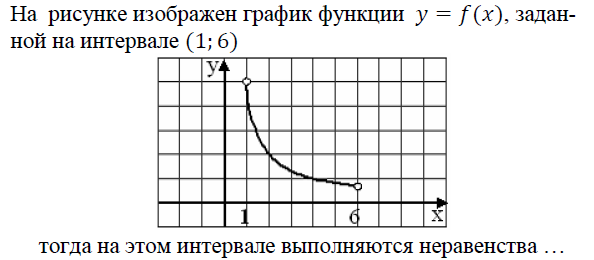
а)
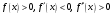 ;
;б)
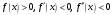 ;
;в)
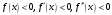 ;
;г)