1.2.2.5 Шар массой 4 кг имеет радиус R = 13 см, вращается вокруг оси симметрии согласно уравнению φ = A + Bt² + Ct³. Определите момент сил М для времени t = 3с. Принять значения B = 2 рад/с; С = - 0,5 рад/сРешение:Момент инерции шара радиуса R, относительно оси, проходящей через его центр определяется по формуле: 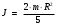(1).Момент сил действующий на шар определим по формуле:M = J⋅ε    (2).ε – угловое ускорение. Первая производная от углового перемещения даст угловую скорость, вторая – угловое ускорение.φ = A + 2t² ‒ 0,5t³φ′ = ω = 4 ⋅ t − 1,5 ⋅ t², ω′ = ε = 4 – 3 ⋅ t   (3).Определим угловое ускорение, в (3) подставим  t = 3 с. 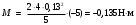ω′ = ε = 4 – 3 ⋅ 3 = ‒ 5      Подставим (1) и (3) в (2) определим момент сил.1.2.3.1 Определите момент инерции J тонкого однородного стержня длиной l=50 см и массой 360 г относительно оси, перпендикулярной стержню и проходящей через: 1) конец стержня; 2) точку, отстоящую от конца стержня на 1/6 его длиныРешение:Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J₀ относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями.

1. 
   Определим момент инерции через конец стержня:
   

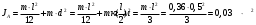
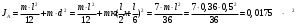
2) Определим момент инерции через точку, отстоящую от конца стержня на 1/6 его длины.1.2.4.1 Платформа, имеющая форму сплошного однородного диска, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше платформы. Определите, во сколько раз

---

измениться угловая скорость вращения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы.

Примечание. Задачу решить с применением закона сохранения момента импульса

Решение:

Для решения задачи применим закон сохранения момента импульса. Закон сохранения момента импульса вытекает из основного уравнения динамики вращательного движения тела, закрепленного в неподвижной точке, и состоит в следующем:
Если результирующий момент внешних сил относительно неподвижной точки тождественно равен нулю, то момент импульса тела относительно этой точки с течением времени не изменяется.

Момент импульса определяется по формуле:

L = J∙ω   (1).

ω – угловая скорость. J – момент инерции.

J₁∙ω₁  =  J₂∙ω₂   (2).

Момент инерции скалярная величина. Определим суммарный момент инерции в каждом случае относительно перпендикулярной оси, проходящей через центр большего диска.
Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J₀ (J₀ – момент инерции диска с человеком) относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния r между осями:

J₁ = J₀+J₀₁,

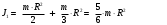(3),

J₂ = J₀ + J₀₂,

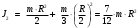(4).



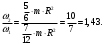
Угловая скорость увеличится в 1,43 раза.

---

Смотрите также файлы

• Развитие пенсионных систем в развитых странах мира и России. Абдуллина Алия.pptx

• Методические рекомендации по написанию практикума соответствуют рабочей программе дисциплины Административное право и Административнопроцессуальное право.pdf

• Каковы рекомендации врача.doc

• 1. зачетные соревнования на учебных занятиях.docx

• Экономическое обоснование путей выхода предприятия из кризисного состояния.docx