МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА (МИИТ)»

Институт Экономики и Финансов

Кафедра «Информационные системы цифровой экономики»

Курсовая работа

по дисциплине «Методы оптимальных решений»

на тему

«Модели организации и планирования производства»

Вариант №1

Выполнил(а):

Студент гр.ЭСБ-241 Александровский С.А.

Проверил: доц. Фроловичев А.И.

Москва – 2023

Содержание

---

ВВЕДЕНИЕ

В процессе управления используется множество разных образов, подходов и приемов, которые позволяют упорядочить, целенаправленно и эффективно организовать выполнение функций, этапов, процедур и операций, необходимых для принятия решений. В совокупности они выступают как методы управления, под которыми понимаются образы осуществления управленческой деятельности, которые создаются для постановки и достижения ее цели.

Математические методы занимают особое место в управлении, поскольку на их основании происходит взаимное обогащение теории и практики управления. Действительно, отвечая на вопрос, как выполнять ту или другую управленческую работу, методы позволяют сформировать систему правил, приемов и подходов, которые сокращают расходы времени и других ресурсов на реализацию.

Оптимальные (эффективные) решения позволяют достигать цели при минимальных затратах трудовых, материальных и сырьевых ресурсов.

В классической математике методы поиска оптимальных решений рассматривают в разделах, связанных с изучением экстремумов функций, в математическом программировании.

Методы оптимальных решений является одним из разделов исследования операций, используемого для решения практических организационных задач. Задачи математического программирования находят применение в различных областях человеческой деятельности, где необходим выбор одного из возможных образов действий (программ действий).

Среди методов математического программирования наиболее полно разработанными и распространенными в производственной практике являются методы линейного программирования.

Целью данной курсовой работы является овладение математическими методами решения экономических задач.

Линейное программирование — это наука о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения. Для решения задач линейного программирования составляется математическая модель задачи и выбирается метод решения. По типу решаемых задач методы разделяются на универсальные и специальные.

ОСНОВНАЯ ЧАСТЬ

Кейс-задание №1

Предприятие может выпускать две марки стали: сталь марки А и сталь марки B. Норма расхода сырья, времени работы оборудования и затрат на электроэнергию, которые необходимы для производства одной тонны каждого изделия, приведены в таблице.

---

Недельные запасы ресурсов, которыми располагает предприятие, ограничены. По сырью эти ограничения обусловлены финансовыми средствами, емкостью складских помещений, логистическими ограничениями и т.д., по оборудованию – плавильными мощностями и трудовыми ресурсами, по электроэнергии – техническими и финансовыми причинами. Размеры запасов и прибыль от реализации продукции в у.е. за 1 тонну приведены в таблице 1.

Исходная таблица

Ресурсы	Нормы расхода ресурсов на тонну продукции		Ограничения по ресурсам
	Сталь марки A	Сталь марки B
Сырье, ед.	0,55k	0,75k	3200+20k
Оборудование	0,45k	0,6k	2100+30k
Электроэнергия	0,4k	0,7k	2100+25k
Прибыль (у.е./т)	90	140

Таблица со значениями из варианта

	Нормы расхода ресурсов на тонну продукции			Ограничения по ресурсам
Ресурсы	Сталь марки A	Сталь марки B
Сырье, ед.	0,55	0,75	3220
Оборудование	0,45	0,6	2130
Электроэнергия	0,4	0,7	2125
Прибыль (у.е./т)	90	140

Требуется сформировать недельную производственную программу (определить объемы выпуска каждого вида продукции), при которой прибыль от реализации будет максимальной.

графический метод;

Построение математической модели. Критерий оптимальности – максимальный доход.

---

Переменные решения:

х1 – сталь марки A (тонн);

х2 – сталь марки B (тонн);

Цель – максимизация прибыли, получаемая при двух видов стали.

Целевая функция:

Z(X) = 90х₁+140х₂max

Ограничения по запасам ресурса на три вида продукции.

Левая часть ограничения по нормам расхода ресурсов представляет собой сырье, оборудование и электроэнергию, затрачиваемые на производство объема выпуска каждого вида крепежных изделий х1, х2. Правая часть ограничения – это их запас ресурса. Получаем следующие ограничения:

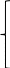- по сырью:

0,55х₁ + 0,75х₂ ≤ 3220

- по оборудованию:

0,45х₁ + 0,6х₂ ≤ 2130

- по электроэнергии:

0,4х₁ + 0,7х₂ ≤ 2125

Вид математической модели:

Z(X) = 90х₁+140х₂  max





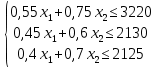
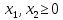
Для построения графической системы необходимо решить неравенства. Для этого приравняем каждое из неравенств и решим их по отдельности.

1)

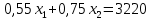
х1	0	5854,5
х2	4293,3	0

2)

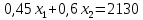
х1	0	4733,3
х2	3550	0

3)

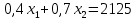
х1	0	5312,5
х2	3035,7	0

Исходя их нашей целевой функции задачи Z(X) = 90х₁+140х₂  max, можем найти вектор-градиент. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации Z(X). Начало вектора – точка (0; 0), конец – точка (90;140).

grad = (90;140)



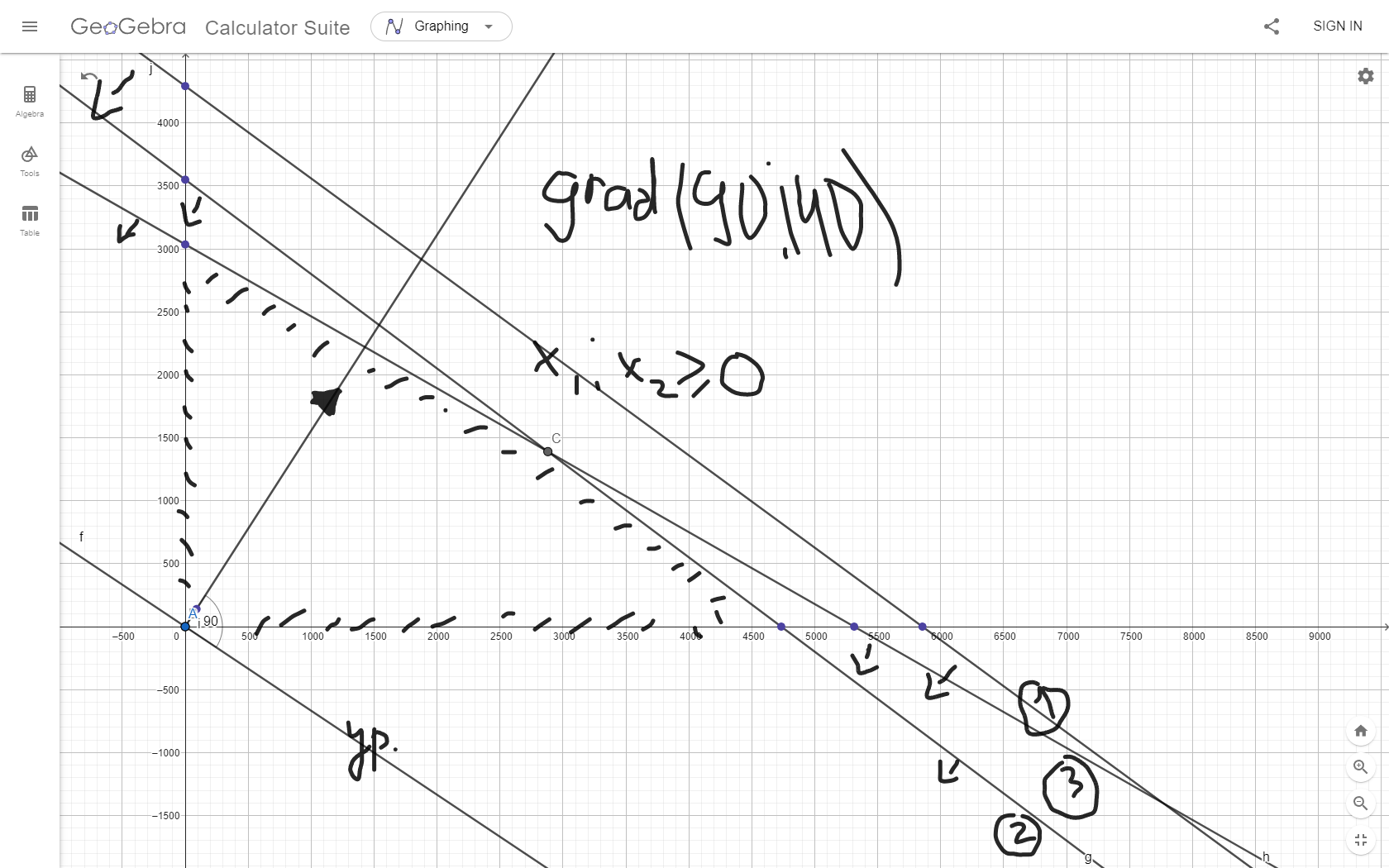
(Графическое решение)

---

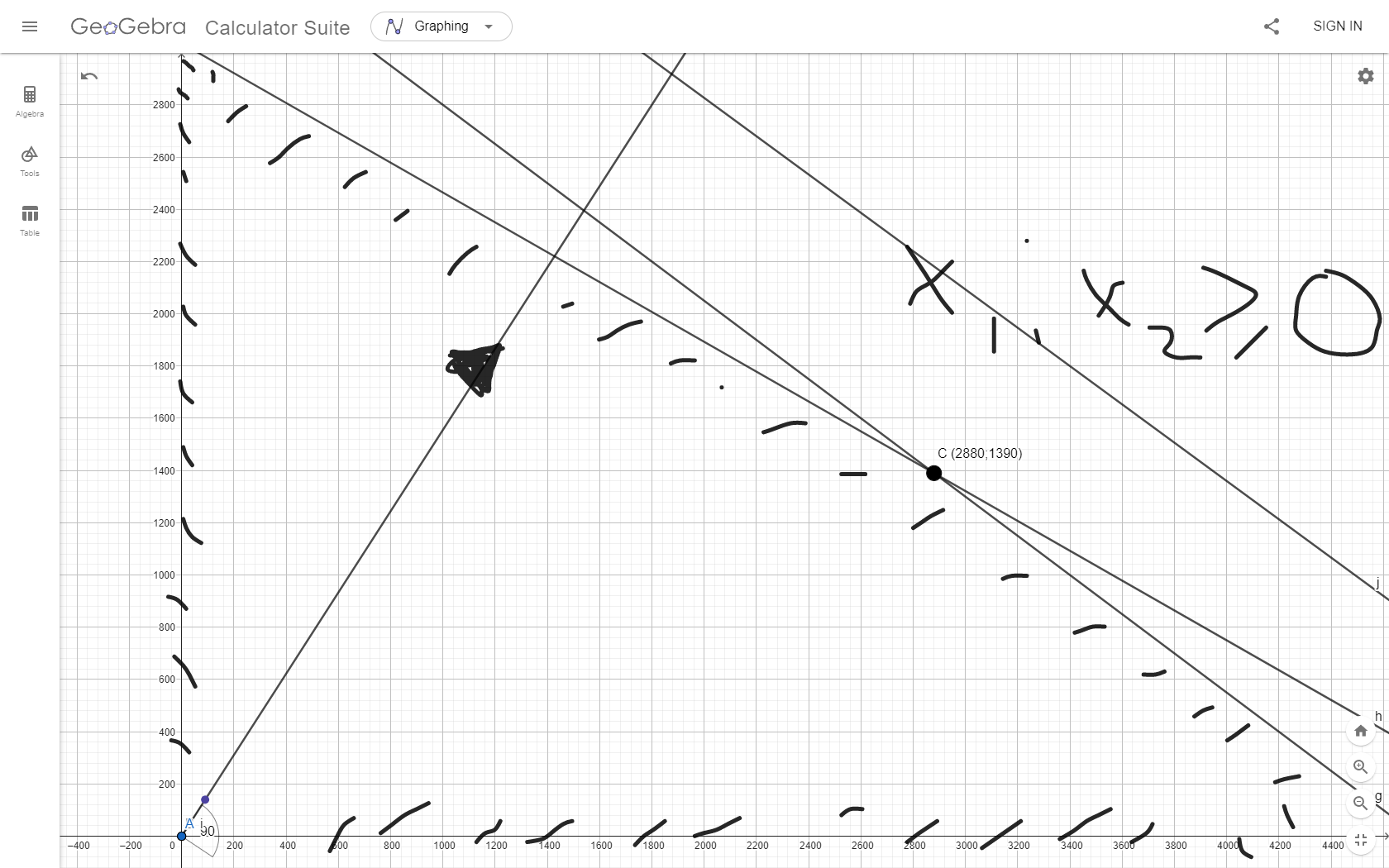
(Выбор точки максимума)

Если вести линию уровня перпендикулярно вдоль нашего grad (90;140), то мы получим точку максимума C с координатами (2880;1390). Данная точка находится на пересечении 2 и 3 прямых. Решив систему уравнений из уравнений, мы проверим данную точку.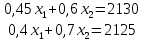



Решив систему уравнений, получим:

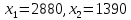
Теперь найдем максимальное значение функции:

Z(X) = 90х₁+140х₂  max

90*2880+140*1390 = 453800

Ответ: 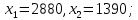Z(X)= 453800

использование надстройки «Поиск решения» MSExcel.

Построив математическую модель, можно перейти к построению табличной модели. Для этого введем данные – параметры, которые характеризуют выпуск крепежных изделий, в единую таблицу.



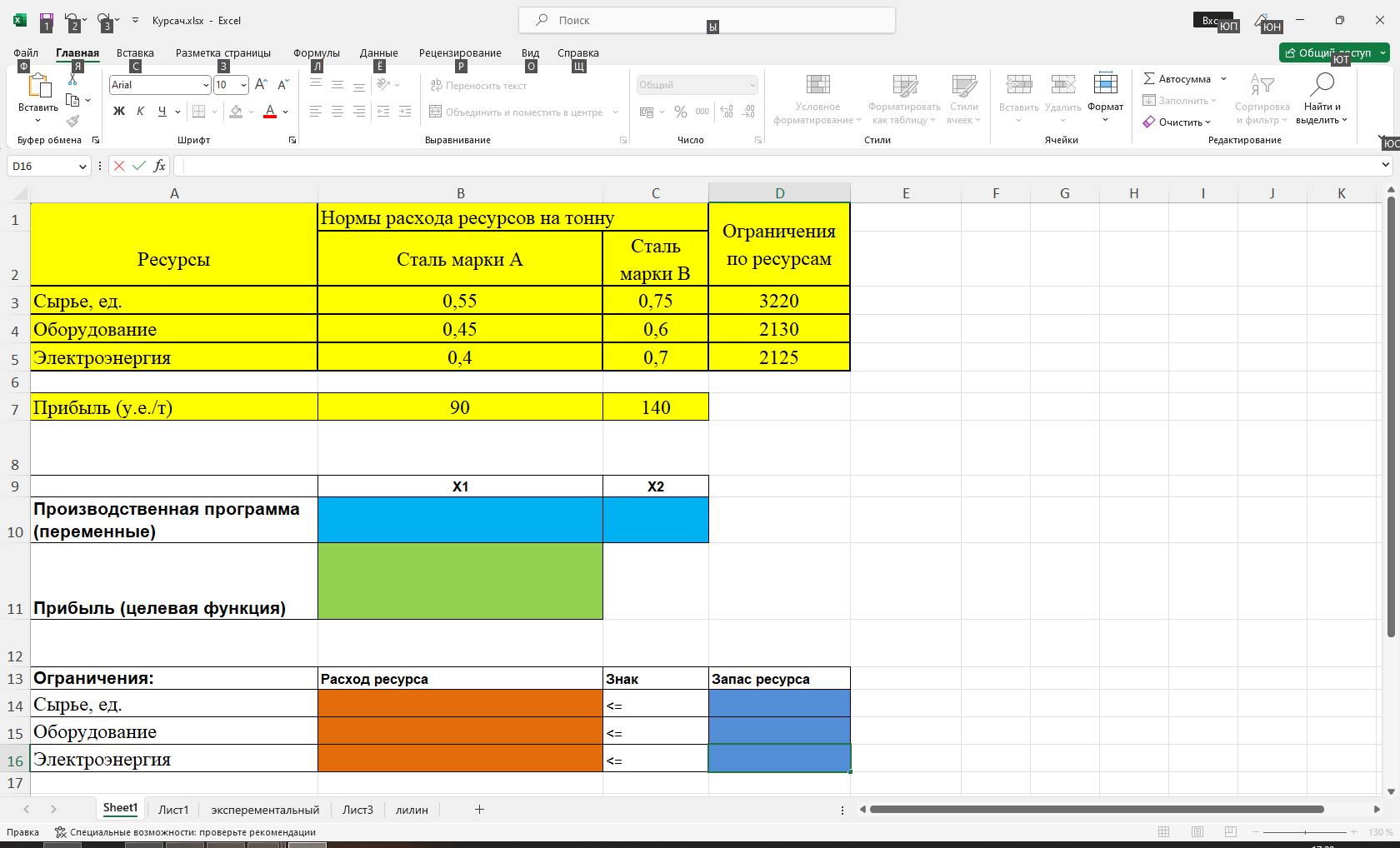
(Исходные данные в табличной модели)

В колонке «Запас ресурса» указаны ограниченные месячные запасы ресурсов, которыми располагает предприятие.

Целевая функция. В ячейке В11 будет отображаться значение целевой функции. Формула, по которой это значение будет рассчитано, определяется выражением:

90х₁+140х₂

Используя обозначения соответствующих ячеек в Excel, получим следующее:

=СУММПРОИЗВ(B10:C10;B7:C7)

Ограничения задачи представляют собой сумму произведений каждой из ячеек переменных (B10, C10) на соответствующую ячейку для коэффициентов конкретного ограничения (B7, C7).

Таким образом, для первого ограничения в ячейку В14 будет введена формула:

=СУММПРОИЗВ($B$10:$C$10;B3:C3),

где символ $ означает, что при копировании этой формулы в другие места листа Excel номер строки 10 не изменится. Скопируем эту формулу в ячейки В15 и В16. В формуле будет меняться только номер строки во втором массиве. Этот номер является строкой, где записано ограничение.



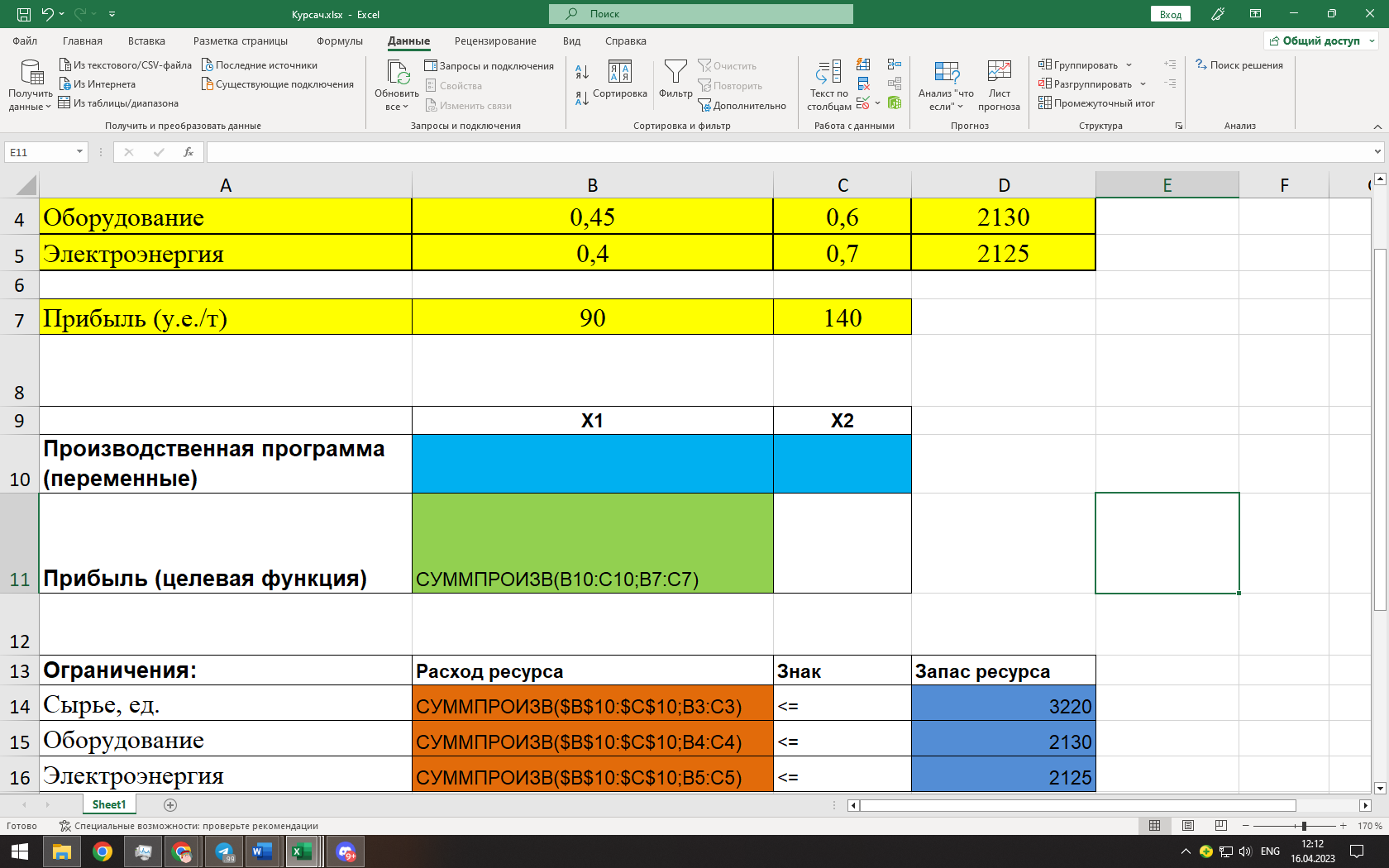
(Ячейки с заполненными формулами)

С помощью надстройки «Поиск решения» найдем решение данной задачи. В диалоговом окне «Поиска решения» требуется ввести необходимые параметры.

---

Смотрите также файлы

• Соглашение об уплате алиментов.docx

• Донесение о пожаре.docx

• Министерств.docx

• Общая информация. Ооо ПетербургГаз.docx

• Пособие для родителей по развитию речи детей от 0 до 2 лет.pdf