ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 55
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В тоже время видим, что наше производство имеет остатки по Сырью. Его расход не превышает запасы, наоборот он меньше.
Таким образом процесс производства прерывается из-за лимита по Оборудованию и Электроэнергии, но не из-за Сырья, это говорит о том, что если увеличить запасы Оборудования и Электроэнергии, но не увеличивать запасы Сырья, то мы все равно сможем произвести дополнительные единицы продукции.
Вывод: Дефицитные ресурсы: Оборудование; Электроэнергия. Избыточные ресурсы: Сырье
Б). Насколько можно уменьшить запасы избыточных ресурсов, чтобы программа производства не пострадала?
Как мы выяснили в предыдущем пункте данной работы, наше производство, создающее продукцию из нескольких видов ресурсов, не полностью использует все из них. Это означает, что часть запасов может быть уменьшена для того, чтобы использовать ресурсы полностью, не оставляя их на складе.
Такой подход может быть оправдан на реальном производстве при, ведь это может помочь уменьшить издержки на закупку сырья, позволит отказаться от аренды дополнительных складских помещений и т.д.
Перейдем непосредственно к переоценке запасов и их оптимизации. Как было установлено ранее, Сырье является избыточным ресурсом, это означает, что запасы можно ограничить без ущерба производству.
Сами запасы по изначальному условию задачи равны 3220 единиц. А использование при оптимальном производстве, то есть максимизации прибыли равен 2626,5 ед.
Итого мы имеем:
3220-2626,5=593,5
593,5 это те самые избыточные единицы, которые не участвуют в производстве и от них можно отказаться, и это не скажется на производственной программе и, следовательно, на нашей прибыли.
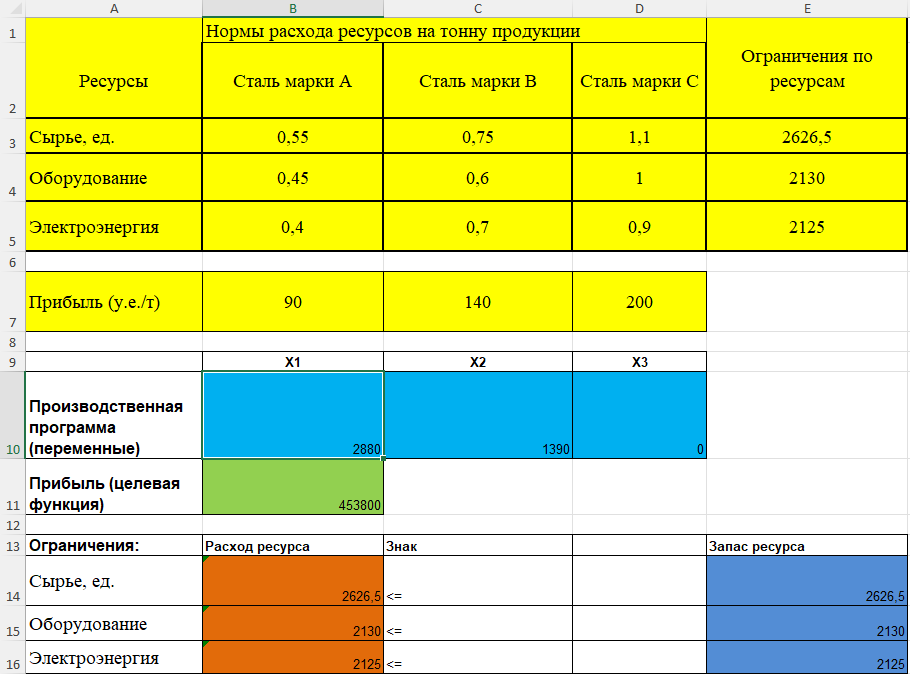
(Производство при сокращении избыточных ресурсов)
Как видим при уменьшение запасов Сырья на 593,5 единицы производственная программа никак не изменилась, прибыли и количество произведенных единиц также не пострадало.
Вывод: при уменьшение такого избыточного ресурса как Сырье на максимально возможные 593,5 единицы, производственная программа и прибыль не меняются.
В). Как изменится производственная программа и прогнозируемая прибыль при увеличении запасов дефицитных ресурсов на 5%
Нами было уже установлено, что дефицитными ресурсами являются Оборудование и Электроэнергия.
| Ресурсы | Изначальные ограничения по ресурсам | Увеличенные на 5% | |
| | |||
| Оборудование | 2130 | 2130+106,5=2236,5 | |
| Электроэнергия | 2125 | 2125+106,25=2231,25 | |
Таким образом мы получаемы таблицу с изменением начальных параметров, а именно запасов. Это позволит произвести больше продукции, а следовательно, увеличить нашу прибыль.
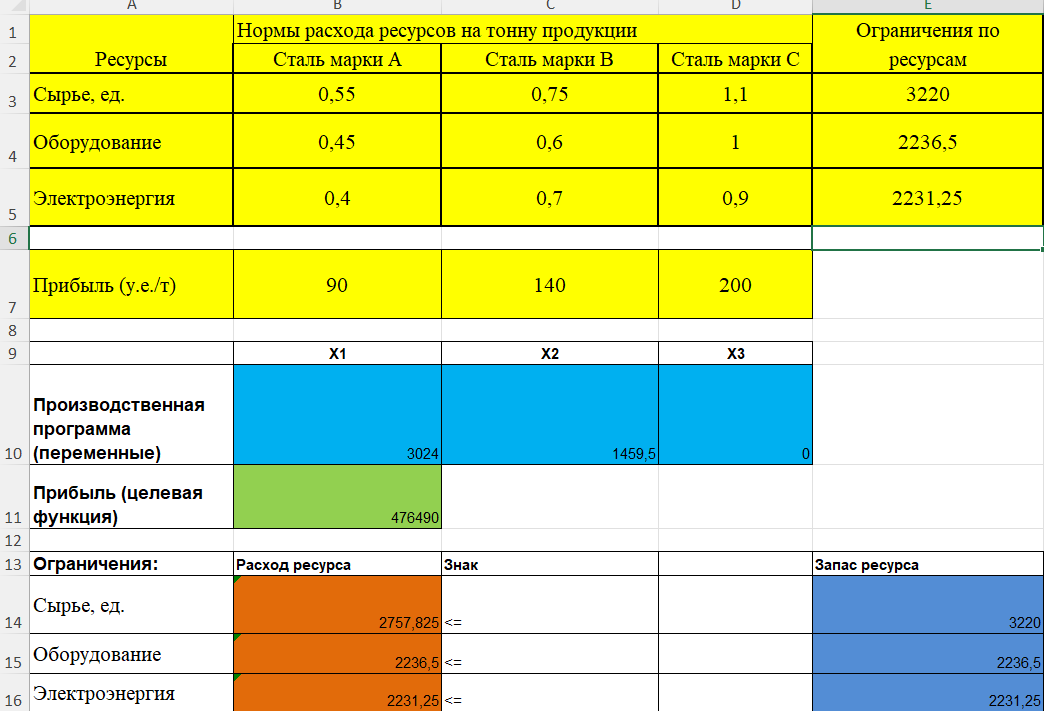
(Измененная программа производства)
Таким образом мы видим, что при незначительном увеличении запасов ресурсов, которых нахватает при производстве, наша производственная программа меняется. Количество произведенных единиц продукции увеличивается, а вместе с ними и полученная прибыль.
Вывод: при увеличении запасов дефицитных ресурсов на 5% мы получаем рост произведенных единиц Стали марки А на 144 единиц; Стали марки B на 69,5; количество единиц Стали марки С осталось нулевым, а прибыль выросла на 22690 условных единиц за тонну.
Г). Как изменится производственная программа при увеличении прибыли, получаемой от стали марки С, на N единиц, где N – число букв в фамилии студента, выполняющего курсовую работу
Изначальной прибылью от Стали марки С является 200 условных единиц за тонну. При увеличении этого показателя производственная программа может существенно измениться, перейдя на более оптимальное и выгодное производство при изменении ситуации на рынке.
Моя фамилия Александровский — это 15 букв. Значит наша N=15.
Итого мы имеем:
200+15=215 (у.е./т)
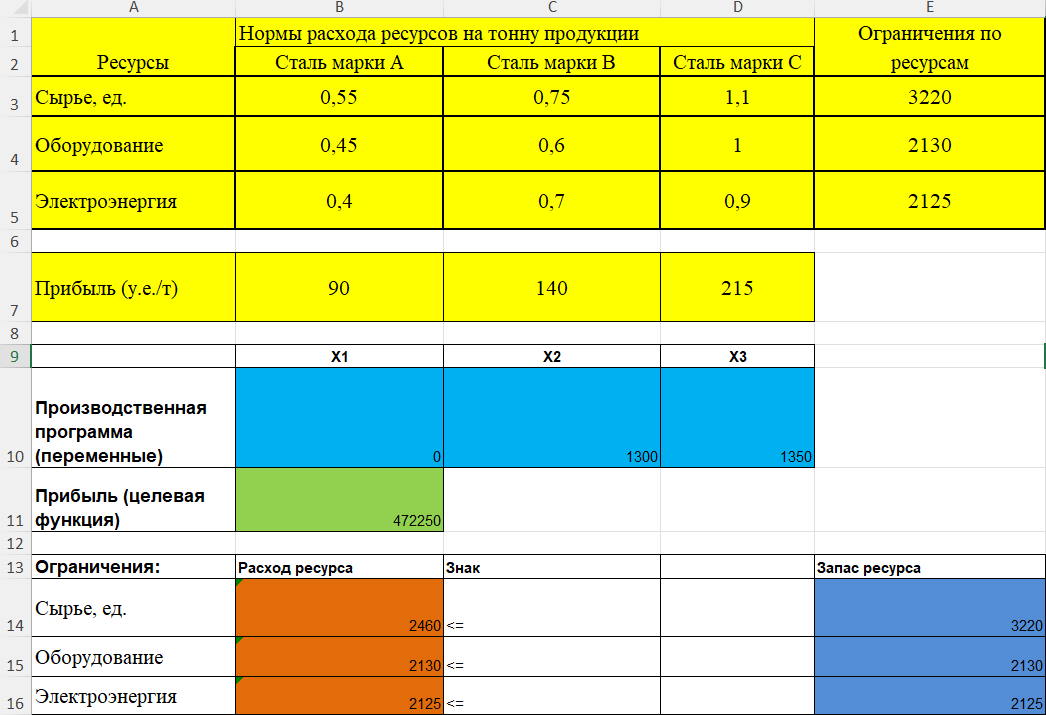
(Измененная программа производства)
После анализа изменений производственной программы мы видим, что приоритет производства сместился. Раньше мы полностью отказывались от производства Стали марки С, так как она была не рентабельна и не окупала затраченных на нее ресурсов в той же мере как и другие марки стали, но после роста ее цены при реализации на 15 единиц, производственная программа поставила приоритет на нее, полностью отказавшись от Стали марки А, ранее производя ее в приоритете.
Таким образом, можно сказать, что при небольших колебаниях на рынке, которые как удешевляют стоимость сырья, так и увеличивают прибыль от продажи изделия, производственная программа должна адаптироваться под изменения, постоянно приспосабливаться к ним и искать оптимальное решение.
Вывод: при увеличении цены за тонну Стали марки С до показателя в 215 условных единиц мы получаем отказ от производства Стали марки А, уменьшение производства Стали марки B на 90 единиц и увеличение производства Стали марки C с 0 до 1350 единиц. Что приводит к увеличению прибыли на 6300 у.е.
ЗАКЛЮЧЕНИЕ
В курсовой работе рассмотрены варианты решений оптимизационных экономических задач методами линейного программирования.
Метод математического программирования является основным инструментом описания оптимальных решений. Оптимальным решением считается такой способ действия, который в наибольшей степени способствует достижению поставленной в задаче цели. Наиболее простыми и лучше всего изученными среди задач математического программирования являются задачи линейного программирования, изучающие методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.
В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решения. Для решения задач линейного программирования разработано сложное программное обеспечение, дающее возможность эффективно и надежно решать практические задачи больших объемов. Эти программы и системы снабжены развитыми системами подготовки исходных данных, средствами их анализа и представления полученных результатов.
Современные методы линейного программирования достаточно надежно решают задачи общего вида с несколькими тысячами ограничений и десятками тысяч переменных. Для решения сверхбольших задач используются уже, как правило, специализированные методы.
В данной курсовой работе были рассмотрены и решены основные задачи линейного программирования по оптимизации производства. Для решения данных задач были применены методы линейного программирования, а именно: графический метод и симплекс-метод, а также использовалась надстройка Microsoft Excel «Поиск решения».
Таким образом выполнение данной курсовой работы показывает, что линейное программирование и методы оптимальных решений могут быть использованы при управление производственными процессами компаний для ускорения и повышения эффективности деятельности организации, а также для увеличения прибыли, что является целью всех коммерческих организаций.
СПИСОК ЛИТЕРАТУРЫ
-
Ишханян М.В., Фроловичев А.И. Методы оптимальных решений: учебное пособие. – М.: МИИТ, 2015. – 132 с. -
Высшая математика для экономистов: учебник для студентов вузов, обучающихся по экономическим специальностям / [Н.Ш. Кремер и др.]; под ред. проф. H.Ш. Кремера. - 3-е изд. - М.: ЮНИТИ-ДАНА, 2010. – 479 с.