ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 56
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(Задача параметров для поиска решений)
(Уведомление о нахождении решения)
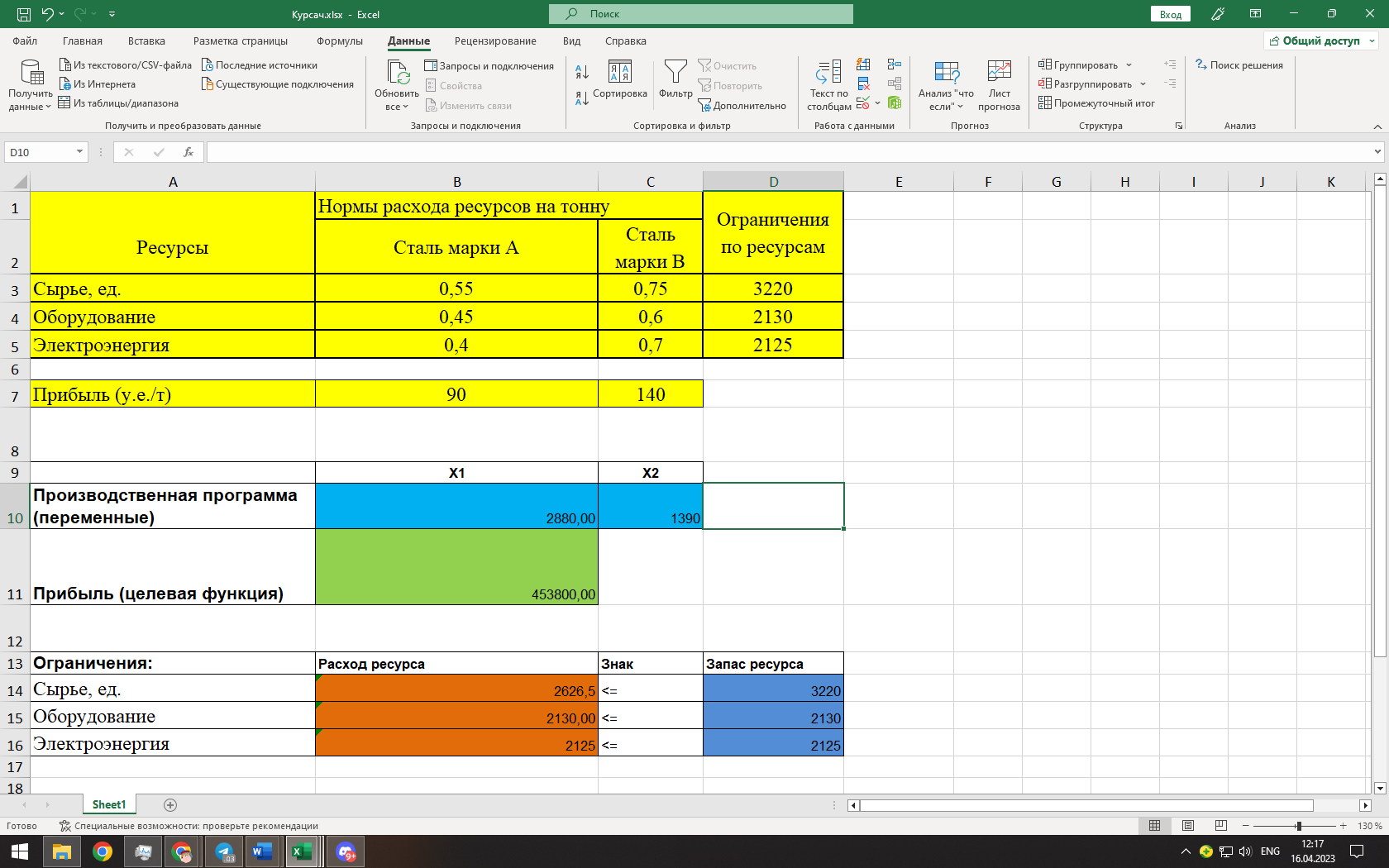
(Результат поиска решений)
Вывод: таким образом в ячейках получается оптимальное решение по производственной программе. При производстве 2880 тонн стали марки A и 1390 тонн стали марки B производство получит максимальную прибыль.
Кейс-задание №2B
Предприятие может выпускать три марки стали: сталь марки А, сталь марки B и сталь марки C. Норма расхода сырья, времени работы оборудования и затрат на электроэнергию, которые необходимы для производства одной тонны каждого изделия, приведены в таблице.
| Ресурсы | Нормы расхода ресурсов на тонну продукции | Ограничения по ресурсам | |||
| Сталь марки A | Сталь марки B | Сталь марки C | |||
| Сырье, ед. | 0,55 | 0,75 | 1,1 | 3220 | |
| Оборудование, ед. | 0,45 | 0,6 | 1 | 2130 | |
| Электроэнергия, ед. | 0,4 | 0,7 | 0,9 | 2125 | |
| Прибыль (у.е./т) | 90 | 140 | 200 | | |
симплекс-метод
Построение математической модели.
Критерий оптимальности – максимальный доход.
Переменные решения:
х1 – Сталь марки A
х2 – Сталь марки B
х3 – Сталь марки C
Цель – максимизация прибыли, получаемая при реализации крепежных изделий: шайб, гаек и болтов. Таким образом, суммарная прибыль, то есть целевая функция:
Z(X) = 90х1+140х2+200х3 max
Ограничения по запасам ресурса на три вида продукции.
Левая часть ограничения по нормам расхода ресурсов представляет собой сырье, оборудование и электроэнергию, затрачиваемые на производство объема выпуска каждого вида крепежных изделий х1, х2, х3. Правая часть ограничения – это их запас ресурса. Получаем следующие ограничения:
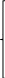- по сырью:0,55х1 + 0,75х2+1,1х3 ≤ 3220;
- по оборудованию:
0,45х1 + 0,6х2 +1х3 ≤ 2130;
- по электроэнергии:
0,4х1 + 0,7х2 +0,9х3 ≤ 2125
Вид математической модели:
Z(X) = 90х1+140х2+200х3 max
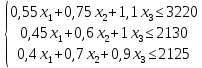
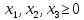
Приведем задачу линейного программирования к каноническому виду:
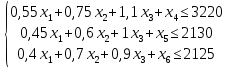
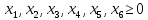
Следовательно: Z1(X)=0-(90х1+140х2+200х3) min
Первый опорный план:
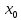= (0,0,0,3220,2130,2125)Базисное решение с помощью следующей симплекс-таблицы:
| | Своб. член | х1 | х2 | х3 |
| Z1 | 0 | 90 | 140 | 200 |
| х4 | 3220 | 0,55 | 0,75 | 1,1 |
| х5 | 2130 | 0,45 | 0,6 | 1 |
| х6 | 2125 | 0,4 | 0,7 | 0,9 |
Нашли генеральный элемент – 1, так как в строке Z выбираем положительное число (у нас число 200 – выбираем столбец х3), а в столбце х3, не считая строки Z, выбираем то значение, для которого отношение к нему свободного члена минимально (2130/1 – минимальное значение). В новом допустимом базисном решении х
3 и х5 изменим на противоположные. Найдем это решение, перейдя к новой симплекс-таблице:
| | Своб. член | х1 | х2 | х5 |
| Z1 | -426000 | 0 | 20 | -200 |
| х4 | 877 | 0,055 | 0,09 | -1,1 |
| х3 | 2130 | 0,45 | 0,6 | 1 |
| х6 | 208 | -0,005 | 0,16 | -0,9 |
Текущий опорный план неоптимален, так как в индексной строке находятся положительные коэффициенты.
Определяем генеральный элемент в новой таблице – 0,16. В новом допустимом базисном решении х2 и х6 изменим на противоположные. Найдем это решение, перейдя к новой симплекс-таблице:
| | Своб. член | х1 | х6 | х5 |
| Z1 | -452000 | 0.625 | -125 | -87.5 |
| х4 | 760 | 0.058 | -0,56 | -0.59 |
| х3 | 1350 | 0.47 | -3,75 | 4.375 |
| х2 | 1300 | -0,031 | 6.25 | -5,625 |
Текущий опорный план неоптимален, так как в индексной строке вновь встречается отрицательный коэффициенты. Значит нам предстоит повторный пересчет.
Определяем генеральный элемент в новой таблице – 0,47. В новом допустимом базисном решении х2 и х6 изменим на противоположные. Найдем это решение, перейдя к новой симплекс-таблице:
| | Своб. член | х3 | | х6 | х5 |
| Z1 | -4538000 | -1,33 | | -120 | -93,33 |
| х4 | 593 | 2,13 | | -0,1 | -1,13 |
| х1 | 2880 | 2,13 | | -8 | 9,33 |
| х2 | 1390 | 0,067 | | 6 | -5,33 |
Далее генеральный столбец выбрать нельзя. Значит, оптимальное решение имеет вид:
Хопт= (2880; 1390;0)
Zmin=-4538000
Zmax= 90*2880 +140*1390 +200*0=453800
Вывод: при объеме выпуска 2880 тонн стали марки A, 1390 тонн стали марки B и 0 тонн стали марки C максимальная прибыль от реализации составит 453800 у.е.
использование надстройки «Поиск решения» MSExcel
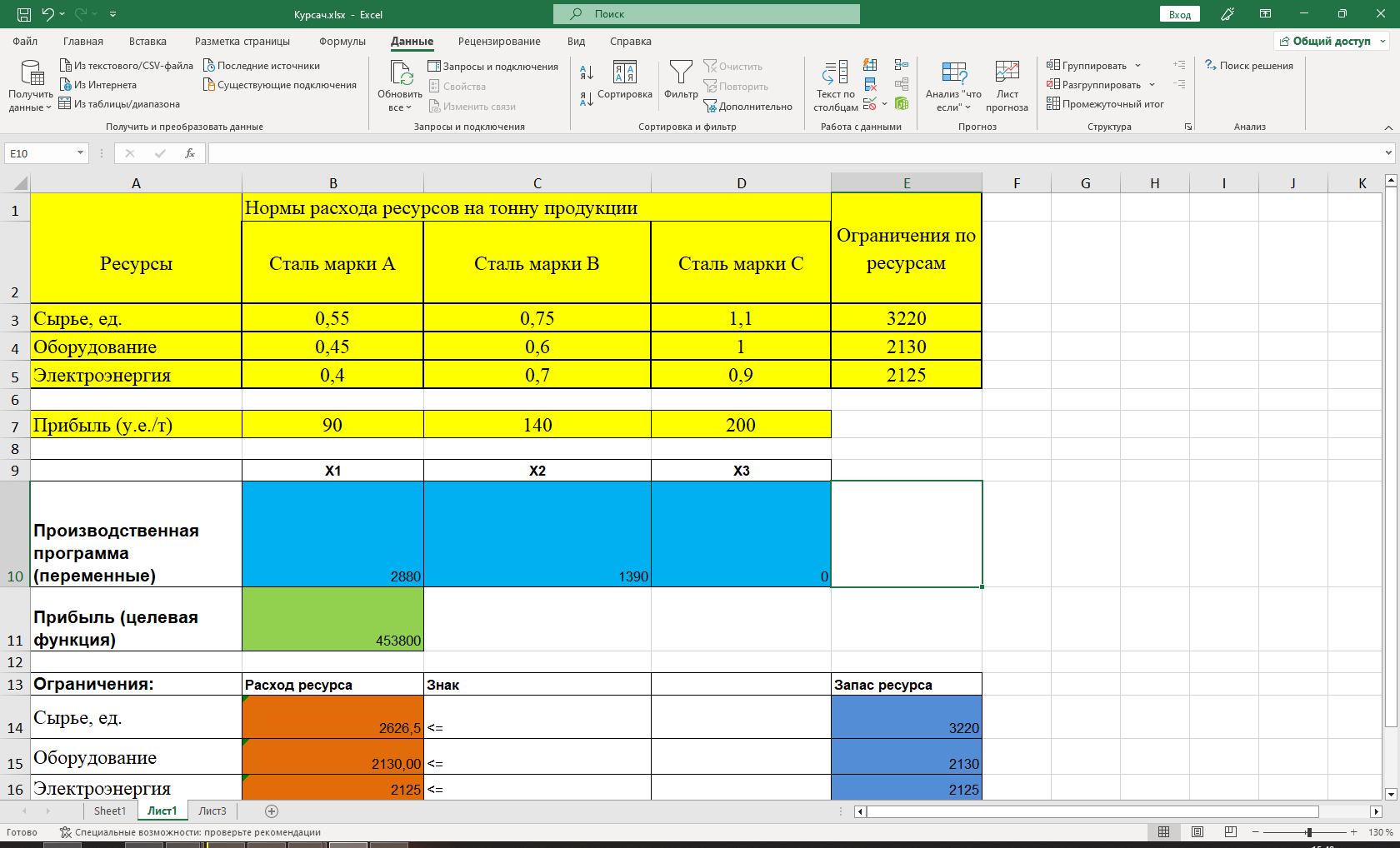
Построив математическую модель, можно перейти к построению табличной модели. Для этого введем данные – параметры, которые характеризуют выпуск стали, в единую таблицу.
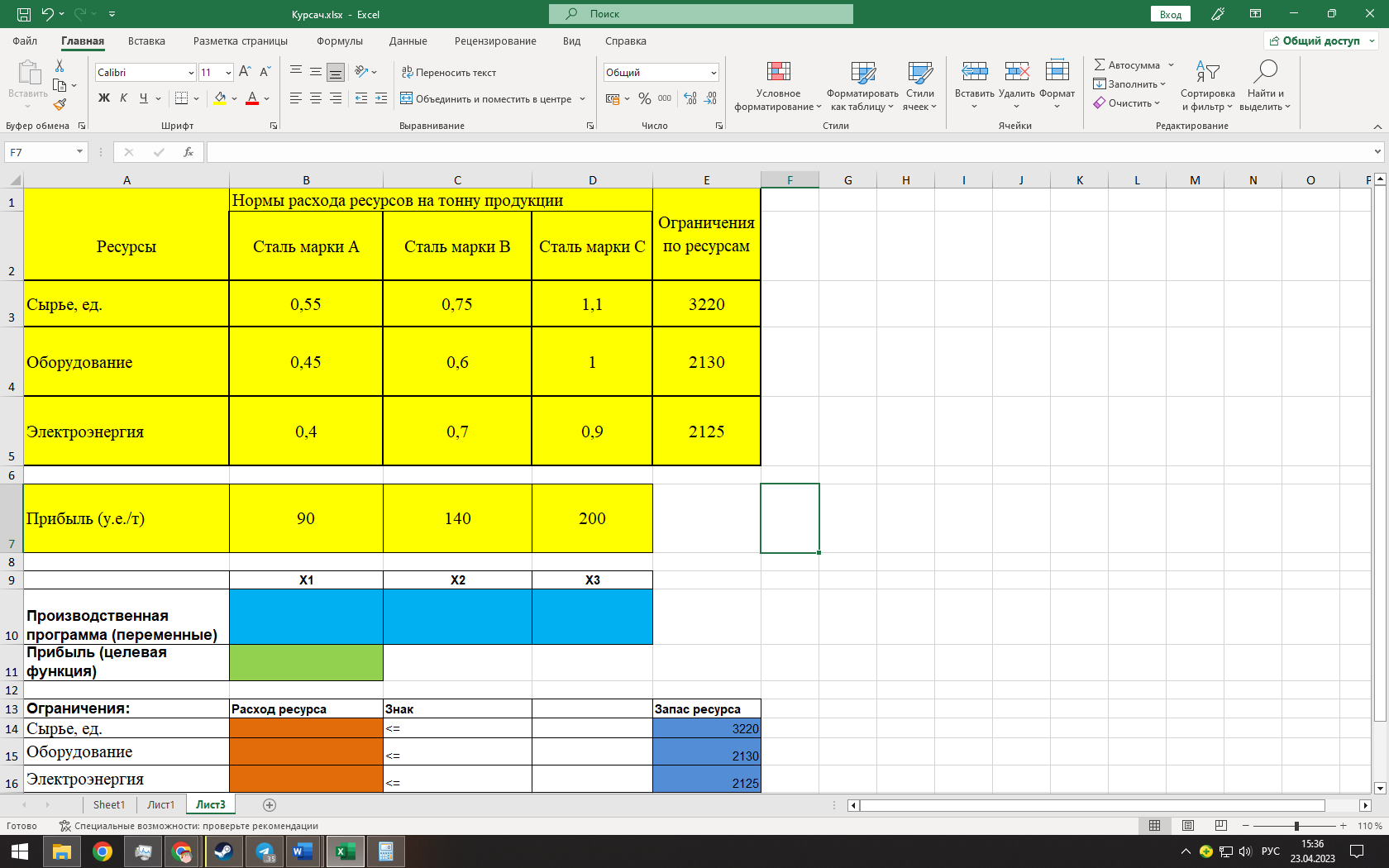
(Исходные данные в табличной модели)
В колонке «Запас ресурса» указаны ограниченные месячные запасы ресурсов, которыми располагает предприятие. Целевая функция. В ячейке В11 будет отображаться значение целевой функции. Формула, по которой это значение будет рассчитано, определяется выражением:
90х1+140х2+200х3
Используя обозначения соответствующих ячеек в Excel, получим следующее:
=СУММПРОИЗВ(B10:D10;B7:D7)
Ограничения задачи представляют собой сумму произведений каждой из ячеек переменных (B10, D10) на соответствующую ячейку для коэффициентов конкретного ограничения (B7, D7).
Таким образом, для первого ограничения в ячейку В14 будет введена формула:
=СУММПРОИЗВ($B$10:$D$10;B3:D3),
где символ $ означает, что при копировании этой формулы в другие места листа Excel номер строки 10 не изменится. Скопируем эту формулу в ячейки В15 и В16. В формуле будет меняться только номер строки во втором массиве. Этот номер является строкой, где записано ограничение.
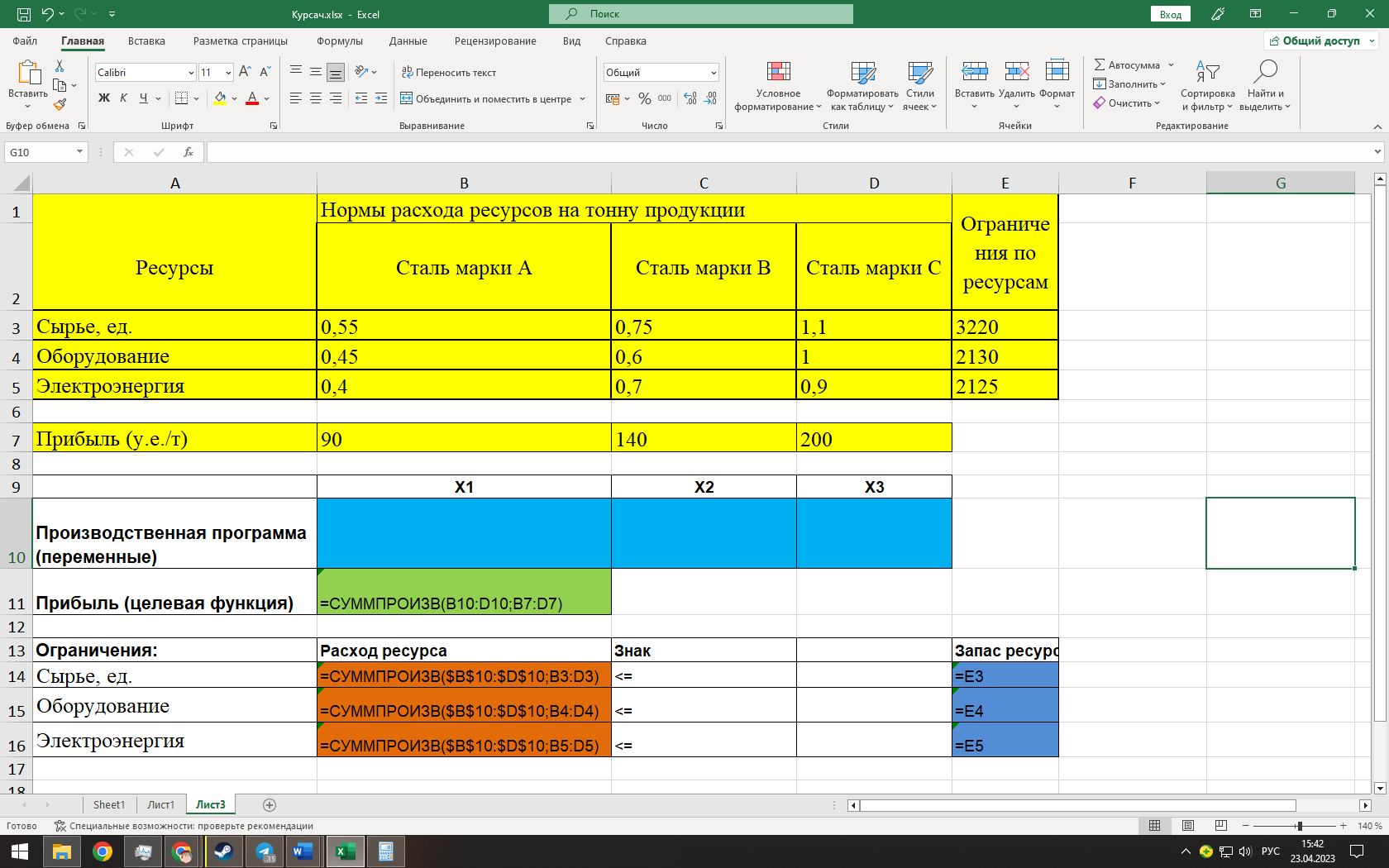
С помощью «Поиска решения» найдем решение данной задачи. В диалоговом окне «Поиска решения» требуется ввести необходимые параметры.
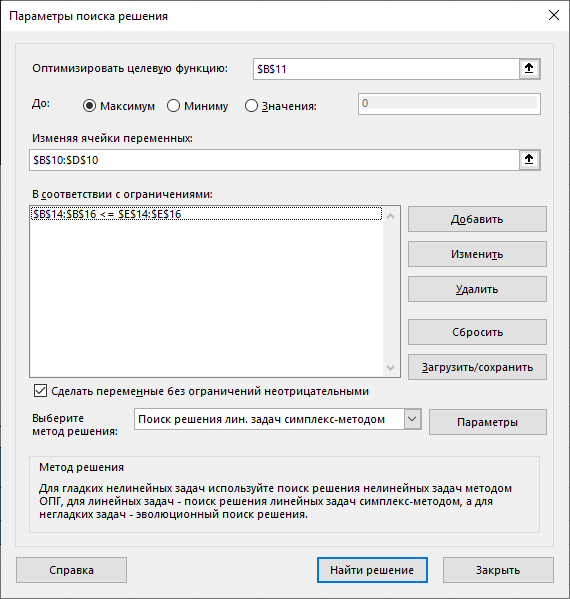
(Задача параметров для поиска решений)
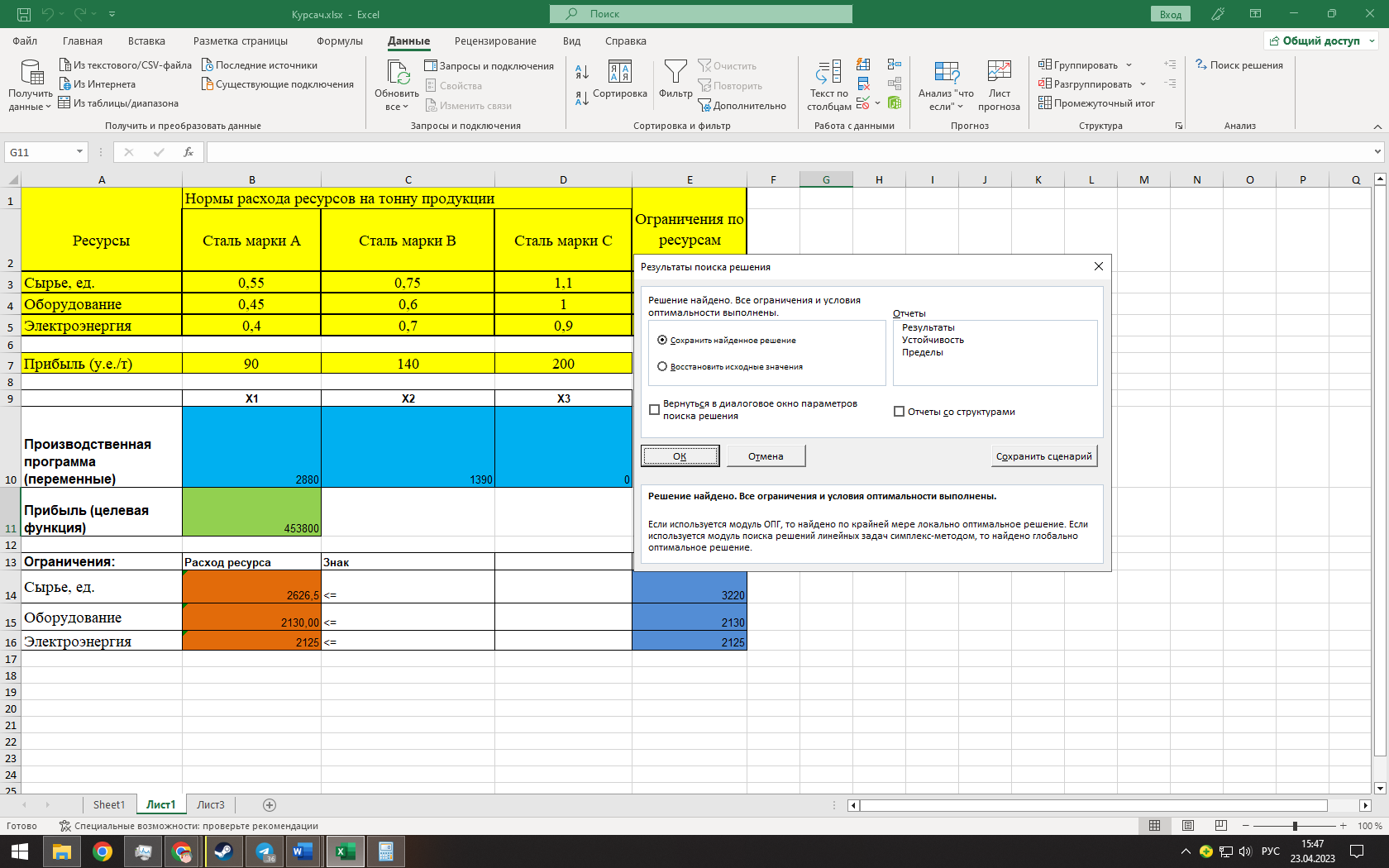
(Выполнение поиска решений)
(Результаты поиска решений)
Вывод: при объеме выпуска 2880 тонн стали марки A, 1390 тонн стали марки B и 0 тонн стали марки C максимальная прибыль от реализации составит 453800 у.е.
дополнительные вопросы оптимальности
А). Определить дефицитные и избыточные ресурсы;
Дефицитные ресурсы — это те ресурсы, которые в соответствии с экономическим принципом нехватки ресурсов или законом о нехватке ресурсов находятся в ситуации ограниченной доступности.
Избыточный ресурс — это ресурс, который имеется в избытке или излишке в системе, и может не может быть использован полностью.
Для полноценного понимания, какие ресурсы являются избыточными/дефицитными, проведем анализ. Удобно будет проанализировать уже готовое решение, которое было представлено нам в предыдущем пункте данной работы.
Основываясь на нем, можно заметить, что все марки стали используют все три вида ресурсов, а именно: сырье, оборудование и электроэнергия. Однако данные ресурсы распределены неравномерно, что-то расходуется в большой степени, что-то в меньшей. Также стоит учитывать запасы ресурсов, тот максимум, который есть на складе и может быть реализован. Более того, нужно понимать, что даже при достатке двух ресурсов, но отсутствии одного сталь не может быть произведена.
Проанализировав данную информацию, можно перейти к определению избыточных и дефицитных ресурсов. Посмотрев на расход ресурсов и их запасы, мы можем заметить, что такие ресурсы как Электричество и Оборудования полностью израсходованы и их запасы полностью истощены.
| Ограничения: | Расход ресурса | Знак | Запас ресурса |
| Сырье, ед. | 2626,5 | <= | 3220 |
| Оборудование | 2130,00 | <= | 2130 |
| Электроэнергия | 2125 | <= | 2125 |