Файл: Друзья, этот файл поможет вам сдать на хороший результат, однако не стоит жадничать сделайте специально пару ошибок Если нужна будет помощь в прохождении других тестов пишите в личные сообщения в матрицах жирным отмечены элементы, по которым искать отве.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 40
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Друзья, этот файл поможет вам сдать на хороший результат, однако не стоит «жадничать» – сделайте специально пару ошибок)))
Если нужна будет помощь в прохождении других тестов – пишите в личные сообщения)
В матрицах жирным отмечены элементы, по которым искать ответ!!!
y = 1 / cosx бесконечно большой функцией …
является при x → п/2
y = 1 / (x + 1) бесконечно большой функцией …
является при x → – 1
y = tgx бесконечно большой функцией …
является при x → п/2
y = cosx бесконечно большой функцией …
не является ни при каком значении x
y = x2 – 4 бесконечно большой функцией …
является при x → ∞
y = ex бесконечно большой функцией …
является при x → + ∞
y = sinx бесконечно малой функцией …
является при x →
y = tgx бесконечно малой функцией …
является при x → 0
y = 1 / cosx бесконечно малой функцией …
не является ни при каком значении x
y = 1 / x бесконечно малой функцией …
является при x → ∞
y = 1 / (x + 4) бесконечно малой функцией …
является при x → ∞
y = √x бесконечно малой функцией …
является при x → 0
y = x2 – 1 бесконечно малой функцией …
является при x → 1
y = ex бесконечно малой функцией …
является при x → – ∞
Абсциссами точек перегиба графика функции … являются:
Абсциссой точек перегиба графика функции … является:
Друзья, этот файл поможет вам сдать на хороший результат, однако не стоит «жадничать» – сделайте специально пару ошибок)))
Если нужна будет помощь в прохождении других тестов – пишите в личные сообщения)
В матрицах жирным отмечены элементы, по которым искать ответ!!!
y = 1 / cosx бесконечно большой функцией …
является при x → п/2
y = 1 / (x + 1) бесконечно большой функцией …
является при x → – 1
y = tgx бесконечно большой функцией …
является при x → п/2
y = cosx бесконечно большой функцией …
не является ни при каком значении x
y = x2 – 4 бесконечно большой функцией …
является при x → ∞
y = ex бесконечно большой функцией …
является при x → + ∞
y = sinx бесконечно малой функцией …
является при x →
y = tgx бесконечно малой функцией …
является при x → 0
y = 1 / cosx бесконечно малой функцией …
не является ни при каком значении x
y = 1 / x бесконечно малой функцией …
является при x → ∞
y = 1 / (x + 4) бесконечно малой функцией …
является при x → ∞
y = √x бесконечно малой функцией …
является при x → 0
y = x2 – 1 бесконечно малой функцией …
является при x → 1
y = ex бесконечно малой функцией …
является при x → – ∞
Абсциссами точек перегиба графика функции … являются:
Абсциссой точек перегиба графика функции … является:
Друзья, этот файл поможет вам сдать на хороший результат, однако не стоит «жадничать» – сделайте специально пару ошибок)))
Если нужна будет помощь в прохождении других тестов – пишите в личные сообщения)
В матрицах жирным отмечены элементы, по которым искать ответ!!!
y = 1 / cosx бесконечно большой функцией …
является при x → п/2
y = 1 / (x + 1) бесконечно большой функцией …
является при x → – 1
y = tgx бесконечно большой функцией …
является при x → п/2
y = cosx бесконечно большой функцией …
не является ни при каком значении x
y = x2 – 4 бесконечно большой функцией …
является при x → ∞
y = ex бесконечно большой функцией …
является при x → + ∞
y = sinx бесконечно малой функцией …
является при x →
y = tgx бесконечно малой функцией …
является при x → 0
y = 1 / cosx бесконечно малой функцией …
не является ни при каком значении x
y = 1 / x бесконечно малой функцией …
является при x → ∞
y = 1 / (x + 4) бесконечно малой функцией …
является при x → ∞
y = √x бесконечно малой функцией …
является при x → 0
y = x2 – 1 бесконечно малой функцией …
является при x → 1
y = ex бесконечно малой функцией …
является при x → – ∞
Абсциссами точек перегиба графика функции … являются:
Абсциссой точек перегиба графика функции … является:
| Функция | Абсцисса |
| y = x3 | 0 |
| y = x3/6 – x2/2 | 1 |
| y = lnx, x > 0 |  |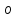
Алгебраическое дополнение элемента y … – см. «Вычислить алгебраическое дополнение элемента y …»
Боковые стороны и меньшее основание трапеции равны по 10 см. Определить ее большее основание так, чтобы площадь трапеции была наибольшей
20 см
Верным является утверждение …
(каждое из этих утверждений является верным)
| 23x – 1 3x ln2 при x → 0 |
| ln(x2 + 1) x2 при x → 0 |
| arcsin(2x) 2x при x → 0 |
| 1 – cosx x2/2 при x → 0 |
Вертикальной асимптотой графика функции … является …
Вертикальными асимптотами графика функции … являются …
| | |
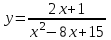 | x = 3; x = 5 |
| y = lnx | x = 0 |
| y = 2/x + x/2 | x = 0 |
Все точки разрыва функции … можно найти как – см. «Точками разрыва …»
Вторая производная функции y = 1/x равна …
2/x3
Вторая производная функции y = sin2x равна …
-4 sin2x
Второй дифференциал функции y = sinx равен …
- sinx dx2
Второй дифференциал функции y = cosx равен …
- cosx dx2
Выберите правильный ответ на вопрос:
производная [c · u(x) – d · v(x)], где c и d – действительные числа, равна
| + c·u`(x) – d·v`(x) | c·u`(x) + d·v(x) | c`·u(x) – d`·v (x) | c·u`(x) + d·v`(x) | 0 |
Вычислить (интеграл) – см. «интеграл … равен» – 2-я половина таблицы
Вычислить алгебраическое дополнение элемента y определителя …
| Определитель | Алгебраическое дополнение y |
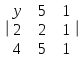 | -3 |
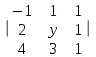 | -5 |
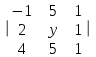 | -5 |
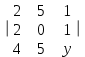 | -10 |
Вычислить минор элемента x определителя – см. «Минор элемента x определителя … равен …»
Вычислить определенный интеграл – см. во второй половине «Интеграл … равен»
Вычислить определитель – см. «Определитель … равен …»
Вычислить приближенно приращение функции y = x2 + 2x + 3, когда x изменяется от 2 до 1,98.
-0,12
Геометрически первая производная от функции
, если она существует, есть
тангенс угла наклона касательной к оси OX
Горизонтальной асимптотой графика функции y = ax является …
y = 0
Дифференциал функции … равен …
| Интеграл | Ответ |
| y = x3 + 3x2 + 3x | (3x2 + 6x + 3) dx |
| y = (ax2 – b)3 | 4ax(ax2 – b) dx |
| y = ln2x |  |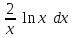
| y = sin22x | 2 sin4x dx |
Дифференциал функции y = x3 при x = 1 и x = 0,1 равен …
0,3
Достаточными условиями существования производной непрерывной функции в точке являются:
существование и равенство двух односторонних пределов
Если = 3, то бесконечно малая по сравнению с бесконечно малой …
одного порядка
Если = 3, то бесконечно малая по сравнению с бесконечно малой …
третьего порядка (верно в другой формулировке)
Заменив приращение функции дифференциалом, приближенно найти sin31°.
0,515
Заменив приращение функции дифференциалом, приближенно найти arctg 1,05.
0,81
Значение функции
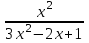при x → ∞ равно …1/3
Значение функции y = e-x при x → + ∞ равно …
равно 0
Из непрерывности функции
еще не следует ее дифференцируемость
Интеграл … равен …
| Интеграл | Ответ |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
| |  |
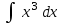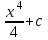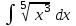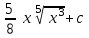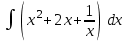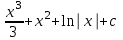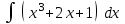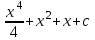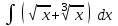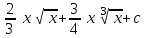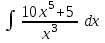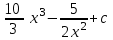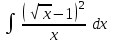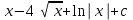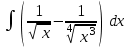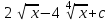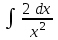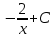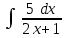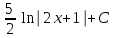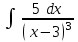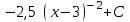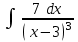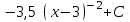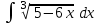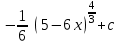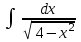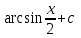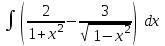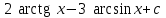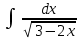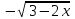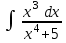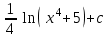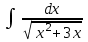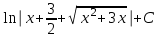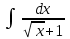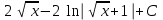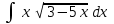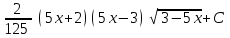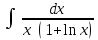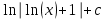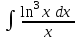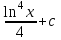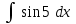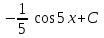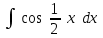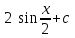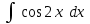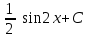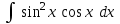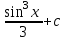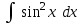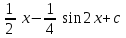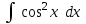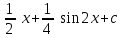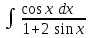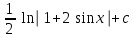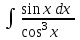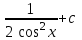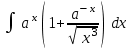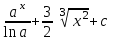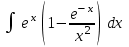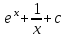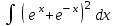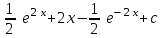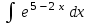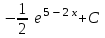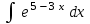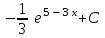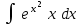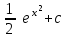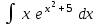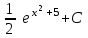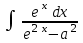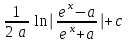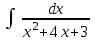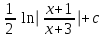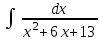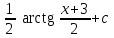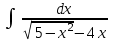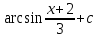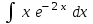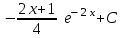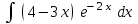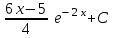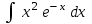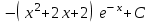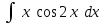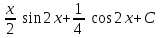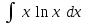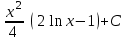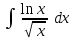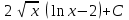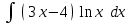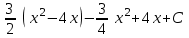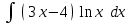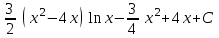| Определенные интегралы | |
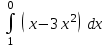 | 1/2 |
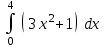 | 68 |
 |  |
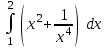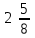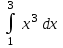 | 20 |
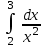 | 1/6 |
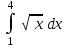 | 14/3 |
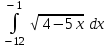 | 64 2/3 |
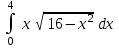 | 21 1/3 |
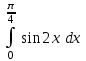 | 1/2 |
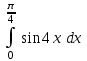 | 1/2 |
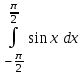 | 0 |
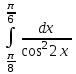 | (√3 – 1)/2 |
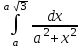 | /12a |
 |  |
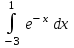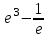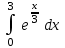 | 3 (e – 1) |
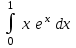 | 1 |
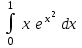 | (e – 1)/2 |
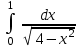 | п/6 |
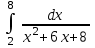 | 1/2 ln5/4 |
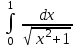 | ln|1 + √2| |
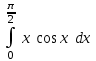 | п/2 – 1 |
 |  |
 |  |
| | |
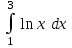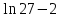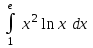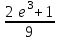Интервалы вогнутости функции
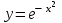можно найти как …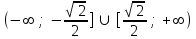
Интервалы выпуклости функции y = x3/3 – 3x2 + 5x + 1 можно найти как …
(– ∞; 3)
Интервалы монотонного возрастания функции … равны …
| Функция | Интервал |
| y = 6x2 – 3x | (1/4; + ∞) |
| y = x3 – 3x2 | (– ∞; 0] U [2; + ∞) |
| y = x/4 + 4/x | (– ∞; – 4] U [4; + ∞) |
| y = x3 – 6x2 + 9x + 3 | (– ∞; 1] U [3; + ∞) |
Интервалы монотонного убывания функции … равны …
| Функция | Интервал |
| y = 3x2 – 12x + 2 | (– ∞; 2) |
| y = x3 – 12x | (-2; 2) |
| y = x3 – 3x2 | (0; 2) |
| y = x3 + 3x2 + 3x + 4 |  |
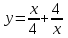 | (– 4; 0] U [0; 4) |