ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 46
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| «Ықтималдық» бөлімі бойынша жиынтық бағалау | Комбинаторика элементтері және оларды оқиғалардың ықтималдықтарын табуда қолданылуы.. Ықтималдықтарды қосу және көбейту ережелері |
| Оқу мақсаты | 10.3.1.2 Қайталанбайтын алмастырулар, орналастырулар және терулерді есептеу үшін формулаларды қолдану 10.3.1.4 Комбинаторика формулаларын қолданып, ықтималдықтарды табуға есептер шығару 10.3.2.4 Ықтималдықтарды көбейту ,қосу ережелерін түсіну және қолдану * P(A ∙ B) = P(A) ∙ P(B) |
| 1- нұсқа 1. Үшеуі бірдей бір түзудің бойында жатпайтын 12 нүкте берілген. а) осы нүктелерден өтетін неше түзу жүргізуге болады? [2] ә) нүктелердің біреуі басы болатын және екінші нүктеден өтетін неше сәуле жүргізуге болады? [2] б)төбелері осы нүктелер болатын неше үшбұрыш жүргізуге болады? [2]
3.Ойыншықтар дүкенінде 100 шар сатылады. Олардың 27-сі көк, 43-і ақ, 8-і қызыл, тағы да сандары бірдей сары және жасыл шарлар бар. Сауранның кездейсоқ жасыл немесе ақ шар алуының ықтималдылығын табыңыз. [4] 4.Есептеңдер: а ) 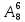  Р4 [2] б) (х+2)4 өрнегінің бином жіктелуіндегі үшінші мүшесін табыңдар.[3] | |
2-нұсқа
1.Үшеуі бірдей бір түзудің бойында жатпайтын 15 нүкте берілген.а) осы нүктелерден өтетін неше түзу жүргізуге болады? [2]
ә) нүктелердің біреуі басы болатын және екінші нүктеден өтетін неше сәуле жүргізуге болады? 2
б)төбелері осы нүктелер болатын неше үшбұрыш жүргізуге болады? [2]
2.1-ден бастап 50-ге дейінгі (50-ді қоса есептегенде) натурал сандардың ішінен кездейсоқ таңдап алынған бір санның жай сан болу ықтималдығын табыңыз. [2]
3.Бір қоймадағыт 10 бұйымның 7-еуі жоғары сапалы,екінші қоймадағы 15 бұйымның 9-ы жоғары сапалы.Әр қоймадағы таңдамай бір-бірден бұйым алғанда екеуінің де сапасыз болу ықтималдығын табыңдар. [4]
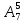
4.Есептеңдер:
Р
5 [2] б) (2х+1)5 өрнегінің бином жіктеліуіндегі төртінші мүшесін табыңдар. [3]