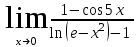
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬУЧРЕЖДЕНИЕ ОБРАЗОВАНИЯКафедра высшей математикиКонтрольная работа по курсуВЫСШАЯ МАТЕМАТИКАВариант 5Проверил: Выполнил:Ф.И.О. преподавателя Ст. гр. № __________Ф.И.О.________________Минск 2023Задание1. Вычислить предел функции по правилу Лопиталя.РешениеПусть функции f и g определены и непрерывны в некоторой окрестност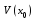и точки 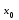за исключением, быть может, самой точки 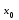. Если существует предел 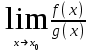, то в целях устранения неопределенност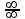и или 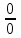можно взять две производные – от числителя и знаменателя. При этом 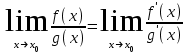значение предела не изменится. Предел 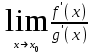тоже должен существовать, в противном случае правило не применимо.Подставим 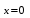и получим неопределенность вида 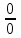.Найдем обе производные, от числителя и знаменателя. 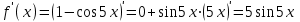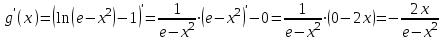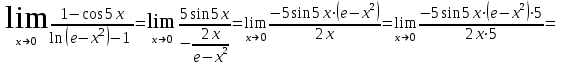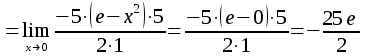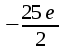;_.Применим правило Лопиталя и получим:_Ответ:Задание2. Вычислить все частные производные второго порядка указанных функций.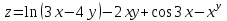_.РешениеНайдем частные производные первого порядка функции z:При нахождении

---

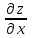
считаем аргумент y постоянным:

.

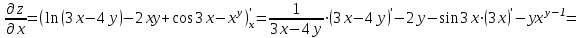
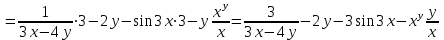При нахождении 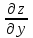считаем аргумент x постоянным: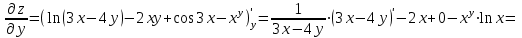



.

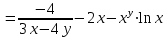Найдем вторые и смешанную частную производную функции z:

Для того, чтобы найти дифференцируем по x: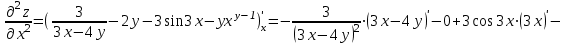

.

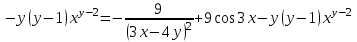Для того, чтобы найти 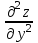дифференцируем 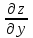по y: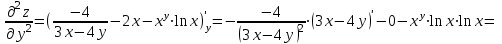



.

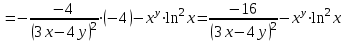Для того, чтобы найти 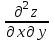дифференцируем по у: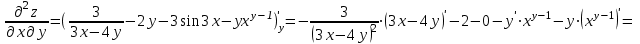



.

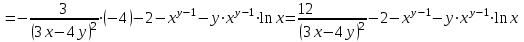Ответ: ;

;

.
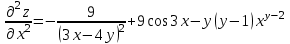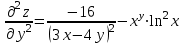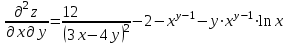Задание3. Вычислить.

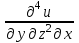, если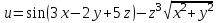

Решение

Для вычисления данной частной производной, необходимо сначала продифференцировать функцию по y, затем 2 раза по z, а затем по x.

При нахождении 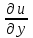считаем аргументы z и x постоянными: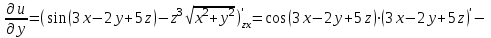



.

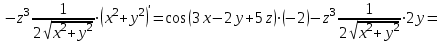
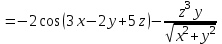При нахождении 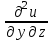считаем аргументы y и x постоянными:

---

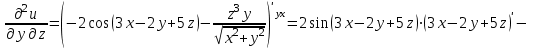
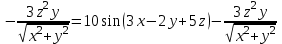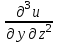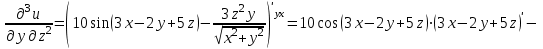
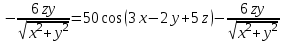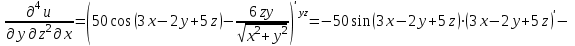
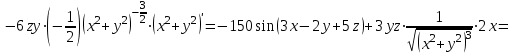
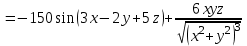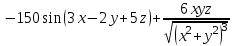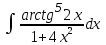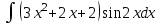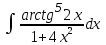
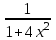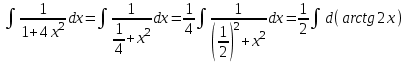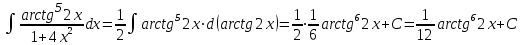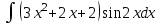
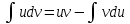
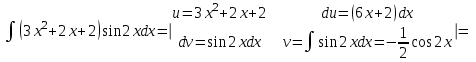
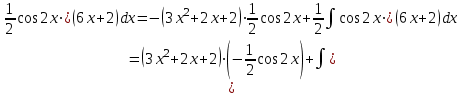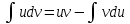
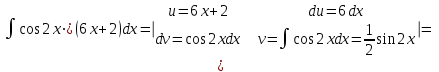
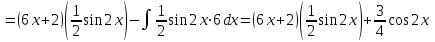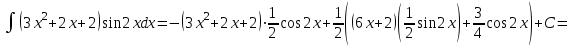
.При нахождении считаем аргументы y и x постоянными: .При нахождении считаем аргументы y и z постоянными: .Ответ: .Задание4. Вычислить неопределенные интегралы:_а) ; б) .Решениеа) Выражение подведем под знак дифференциала, т.е.:_. ._б) К данному интегралу применим метод интегрирования по частям: К полученному интегралу применим метод интегрирования по частям: .Получим: 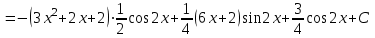.Ответ: а) 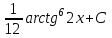;б) 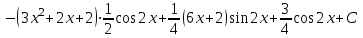.Задание5. Вычислить определенные интегралы:

---

а) 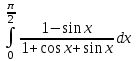; б) .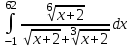

Решение

а) Применяем универсальную тригонометрическую подстановку:

_{; ; ; ; .}





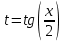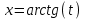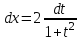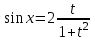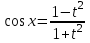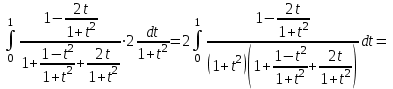
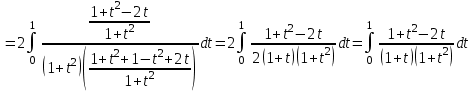
Используем метод разложения на простейшие. Разложим функцию на простейшие слагаемые:



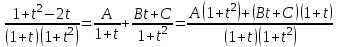
Приравняем числители и учтем, что коэффициенты при одинаковых степенях x, стоящие слева и справа должны совпадать:







.





.

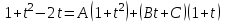
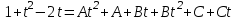
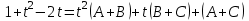
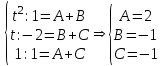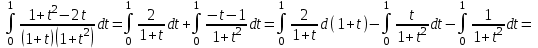
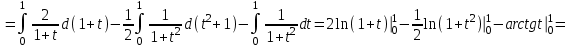
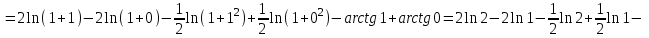
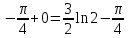б)

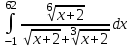
Введем замену: 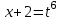, тогда , .



.

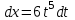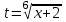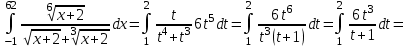
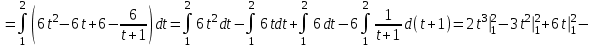
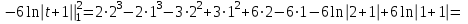
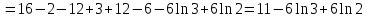Ответ: а) ;

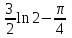б) .
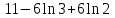Задание6. Найти общее решение дифференциального уравнения:

---

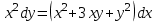
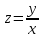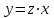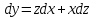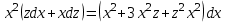
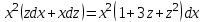
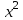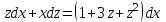
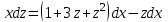
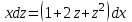
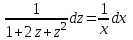
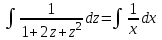
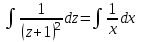
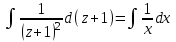
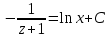
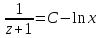
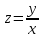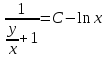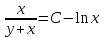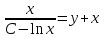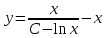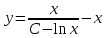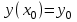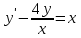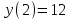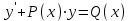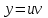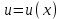РешениеСделаем замену: , , .Получим:Первое решение x=0.Делим обе части на .Проинтегрируем:Учитывая, что , получим: , , , .Ответ: ; x=0.Задание7. Решить задачу Коши при начальном условии : , .РешениеЭто линейное дифференциальное уравнение первого порядка относительно y, и оно имеет вид: .Решение будем искать в виде произведения двух функций , где и 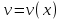- неизвестные функции от переменной x. Тогда

---

Смотрите также файлы

• 1. Раскройте понятие объективного вменения.doc

• Примечание y.pdf

• Рассказу Рэя Брэдбери Каникулы.doc

• Самостоятельная работа по теме 1 Цель занятия закрепление знаний о психологических основах творческой деятельности детей, формирование умения применять их.docx

• Руководитель практики от профильной организации.docx