Файл: Решение Для вычисления данной частной производной, необходимо сначала продифференцировать функцию по y, затем 2 раза по z, а затем по x.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 22
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
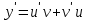. Подставив y и 
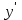в исходное уравнение, получим:
,
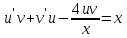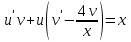
Функцию v найдем так, чтобы выражение в скобках равнялась нулю:
,
,
,
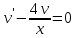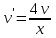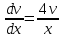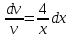
Получили уравнение с разделяющимися переменными. Проинтегрируем обе части и получим:
,
,
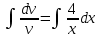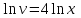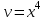.Подставим найденную функцию v в уравнение:
,
,
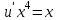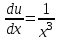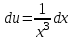.Проинтегрируем обе части и получим:
,
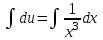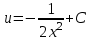.Тогда общее решение исходного дифференциального уравнения будет иметь вид:
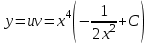.Найдем частное решение при условии:
.
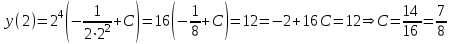.Таким образом, частное решение имеет вид:
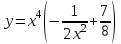.Ответ:
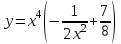.Задание8. Найти общее решение дифференциального уравнения.
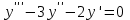
Решение
Это линейное однородное дифференциальное уравнение третьего порядка с постоянными коэффициентами.
Составим характеристическое уравнение и решим его.
; 
; 
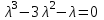
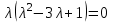
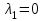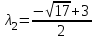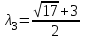.Получили 3 действительных корня.
Общее решение однородного уравнения будет иметь вид:
,
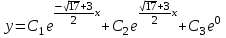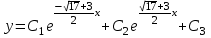.Ответ:
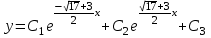.Задание9. Записать первые четыре члена ряда. Исследовать сходимость числовых рядов.
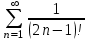
Решение
Запишем первые четыре члена ряда:
При n=1:
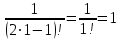.При n=2:
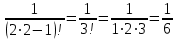.При n=3:
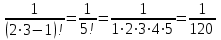.При n=4:
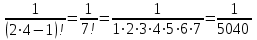.Вычислим интервал сходимости ряда с помощью признака Даламбера:
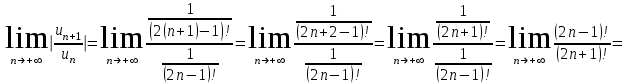
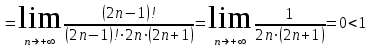, значит, ряд сходится.Ответ: сходится.
Задание10. Найти радиус и область сходимости степенного ряда.
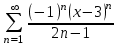
Решение
Вычислим интервал сходимости ряда с помощью признака Даламбера:
.
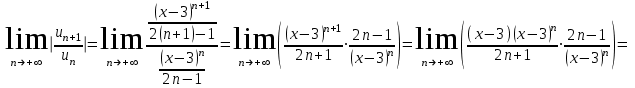
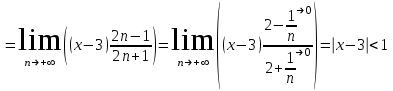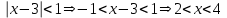.Радиус сходимости:
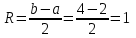.Исследуем сходимость на концах интервала.
-
При x=2:
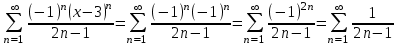. Рассмотрим два положительных числовых ряда
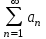и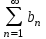 
. Если предел отношения общих членов этих рядов равен конечному, отличному от нуля числу: 
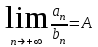, то оба ряда сходятся или расходятся одновременно.Возьмем расходящийся ряд
.
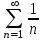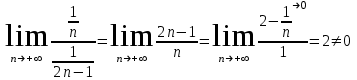, значит, ряд 
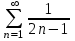тоже расходится.-
При x=4:
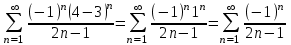.Рассмотрим первые три члена ряда:
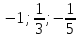.Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется:
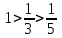.б) По второму признаку Лейбница предел ряда должен стремится к 0.
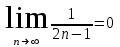.Второе условие Лейбница выполняется.
Таким образом, рассматриваемый ряд сходится.
Но, т.к.
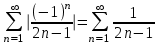расходящийся ряд, то в данной точке ряд сходится условно.Область сходимости степенного ряда
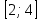.Ответ:
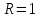, область сходимости степенного ряда .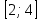