1.Жиындардың берілу тәсілдері.

Жиын ұғымы математиканың негізгі, алғашқы ұғымдарының бірі, сондықтан ол басқа ұғымдар арқылы анықталмайды. Жиындар теориясының негізін қалаған неміс математигі Георг Кантор (1845-1918) жиын түсінігін келесі түрде анықтаған: «Бірнеше заттардың, объектілердің қандай да бір белгісіне қарай біртұтас болып бірігуі жиынды анықтайды». Сан ұғымынан бұрын шыққан жиын ұғымын қандай да бір нәрселердің жинағы ретінде түсінеміз, ол жинаққа кіретін нәрселерді жеке-жеке қабылдауға және оларды бір-бірінен де, бұл жинаққа жатпайтын басқа нәрселерден де ажыратуға болады деп білеміз. Яғни, жиын туралы сөз еткенде, қандай да бір белгілері бойынша бір тұтас етіп біріктірілген нәрселерді қарастырамыз.

Мүшелерін тізіп жазу және сипаттау арқылы.Мүшелерін тізіп жазу арқылы. Бұл тәсілмен тек қана ақырлы жиындарберіледі. Мысалы, процессор a, монитор b, клавиатура c және принтерден d тұратын компьютер А жиынын былай өрнектеуге болады: A = {a, b, c, d}, ақырлы жиын   .Ақырсыз жиындарды тізіммен беру мүмкін емес. Мысалы, барлық натурал сандардың немесе барлық бүтін сандардың жиынын тізім арқылы беру, яғни ол жиындардың барлық элементтерінің тізімін жасау мүмкін емес.

1. 
   
   Ең болмағанда А жиынына немесе В жиынына тиісті элементтер жиынын А және В жиындарының бірігуі (қосындысы)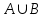   деп атаймыз.
   
2. 
   
   А жиынына да В жиынына да тиісті элементтер жиынын А және В элементтер жиынының қиылысуы (көбейтіндісі) деп аталады.
   

---

7.Группалар,сақиналар,өріс







САҚИНА

Екі амал берілген K жиыны-қосу (+) және көбейту (*), егер келесі шарттар орындалса, сақина деп аталады:

1) қосу операциясына қатысты жиын — K коммутативті топ, яғни.

а)Коммуникативті қосу операциясы: ;

б) Ассоциативті қосу операциясы: ;

в)  нөлдік элемент бар;

г) әр элемент үшін оған қарама қарсы элемент бар;

2)  K жиынына ассоциативті көбейту амалы:

3) қосу және көбейту операциялары дистрибутивті заңымен байланысты:



Өріс

Жиын П, онда екі амал берілген: қосу ( + ) және көбейту ( * ), егер келесі шарттар орындалса, өріс деп аталады:

1) П-бірлігі бар коммутативті сақина  ;

2)  әрбір элементі үшін,  нөлден басқа, кері элемент бар 

---

.

Көріп отырғаныңыздай, өріс — бұл төрт амал анықталған жиын: қосу, көбейту, азайту және бөлу. Мысалы, өрістер рационал және нақты сандар жиыны болып табылады.


13.Ең кіші ортақ еселік (ЕКОЕ)





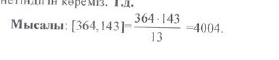
A={ 1, 2, 4, 7, 13, 14, 26, 28, 52, 91, 182, 364}

B={ 1, 11, 13, 143}

AB={1.13}

19. Көпмүшеліктің еселі көбейткіштері бөлу





Теорема 15. F (X) көпмүшесі P (x) өрісінің үстінде P егер және тек егер оның туындысымен өзара қарапайым болса, оның еселіктері болмайды.



Алгоритмі:

1.Туындысын аламыз

2.Евклид алгоритмі бойынша ЕҮОБ табамыз.

3.Д(х) ТУЫНДЫСЫН табамыз,

4.Е ні табамыз

5.Функцияның түрін жазамыз








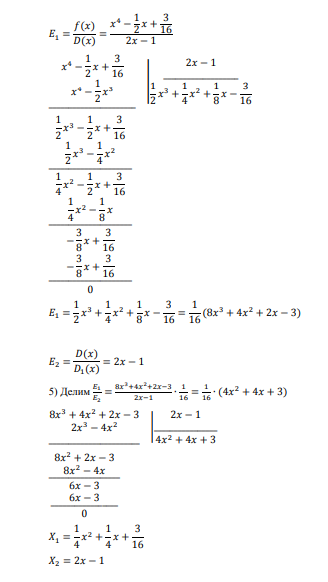
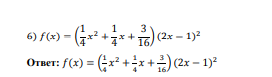
25.Салыстырулар теориясы

Салыстыру теориясы сандар теориясының бір бөлімі. 1795 жылы салыстырудың мәні мен символдық белгілеуін алғаш рет Гаусс енгізді. Оның зерттеу жұмысы 1801 жылы «Арифметикалық зерттеу» еңбегінде көрсетілген. Салыстыру жөніндегі ұғым бір санның екінші санға бөлінгіштігі ұғымымен тығыз байланысты. Бұл ұғым бізге әсіресе берілген сандардың бірі екіншісіне бөлінетін-бөлінбейтінін және де қандай қалдық қалатынын білу керек болғанда аса қажет болмақ.

Математикада салыстыру теориясын көп жерде қолданады. Мысалы, салыстыру теориясы арқылы екі айнымалы бірінші дәрежелі теңдеуді шешуде, санды санға бөлгенде қалдықты табу, арифметикалық амалдың дұрыс орындалғандығын тексеру, жәй бөлшекті ондық бөлшекке айналдырғандағы период ұзындығын табу, тағы сол сияқты мәселелерде қолданады.

---

Анықтама. a және b – бүтін сандар m модулі бойынша салыстырмалы деп аталады, егер a – b айырмасы m-ге бөлінетін болса.

Сонда берілген a, b, m сандары арасындағы қатынасты салыстыру көрсетеді және m –маңызды рөл атқарғандықтан, біз оны «модуль» деп атаймыз. Қысқаша, бұл үш сандардың қатынасын мынандай түрде жазамыз:

a 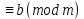(1).

Ал a және b – салыстырудың оң және сол жақтары деп атайды. m саны әрқашан оң мәнге ие: m 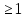және ол модуль таңбасымен жазылады: mod m. Егер a - b айырмасы m-ге бөлінетін болса, онда a 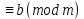түрінде, ал егер бөлінбейтін болса, a 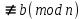түрінде жазамыз.

Салыстыру қатынас:

1. 
   Рефлексивті, яғни a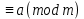
   
2. 
   Симметриялы, яғни a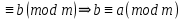
   
3. 
   Транзитивті, яғни
   

---

Смотрите также файлы

• Методические указания по прохождению преддипломной практики Специальность 09. 02. 04Информационные системы (по отраслям).docx

• 2. теория государства и права и другие социальные науки.docx

• 1. Понятие языковой нормы характерно для а литературного языка.docx

• Общие признаки воинского коллектива Воинский коллектив.docx

• 3 Заключение от профильной организации.docx