1.Шынайылықты репрезентативтілік қатесін анықтау арқылы бағалау тәсілі.

Орта шаманың орташа қатесінің формуласы:

, мұндағы σ - ортаквадраттық ауытқу; n – бақылау саны.

Салыстырмалы көрсеткіштің қатесінің формуласы:

, мұндағы p — %, %о,%оо өрнектелген көрсеткіш.

q = (100 – p) егер p - % өрнектелсе; немесе (1000 – p) егер p - %о өрнектелсе;

(10 000 — p) егер p - %оо өрнектелсе және с.с.

Егер бақылау саны 30-дан кіші болса, онда репрезентативтілік қатесінің сәйкес формулалары:

и

2. Орта және салыстырмалы шамалардың сенім шекараларын анықтау.

Сенім шекараларын анықтау формулалары:

Орта шама үшін ( ):_бас=_{таңдама} ± t

Салыстырмалы шамалар үшін (Р): Рбас=Ртаңдама ± t , мұндағы _бас және Рбас — сәйкес бас жиынтықтың орта шамасы мен салыстырмалы көрсеткіштерінің мәндері;

_{таңдама} және Ртаңдама - сәйкес таңдама жиынтықтың орта шамасы мен салыстырмалы көрсеткіштерінің мәндері;

- репрезентативтілік қатесі; t – шынайылық критерийі (сенім коэффициенті).

Бұл тәсіл таңдама жиынтық нәтижелері бойынша бас жиынтықтағы зерттеліп отырған құбылыстың (немесе белгінің) өлшемдері жөнінде пайымдау қажет болған жағдайда қолданылады.

Әдісті қолданудың міндетті шарты таңдама жиынтықтың репрезентативті болуы. Таңдама тәсілдің нәтижелерін бас жиынтыққа аудару үшін сенім ықтималдығының (қатесіз болжау ықтималдығы Р) дәрежесі қажет, ол зерттеліп отырған белгілер бойынша таңдама тәсіл нәтижелері жағдайлардың қанша пайызында бас жиынтықта орын алатындығын көрсетеді.

Орта шаманың немесе салыстырмалы көрсеткіштің сенім шекараларын анықтау барысында сенім ықтималдығының қажетті дәрежесін зерттеуші өзі тағайындайды.

Медициналық-биологиялық зерттеулердің көбісінде сенім ықтималдығының дәрежесі Р=95,5%, жеткілікті деп саналады, яғни бас жиынтықта таңдама тәсіл бойынша анықталған заңдылықтан ауытқу байқалуы мүмкін жағдайлар саны 5%-тен аспайды. Кейбір зерттеулерде, мысалы, жоғарытоксикологиялық заттарды, вакциналарды, оперативті емдеу тәсілдерін және т.б.қолданумен байланысты болатын, нәтижесінде сырқаттың ауыр түрі, асқыну, летальды нәтижелер тууы мүмкін жағдайларда сенім ықтималдығының Р=99,7%, дәрежесі қолданылады, яғни бас жиынтықта 1%-тен аспайтын жағдайлар санында таңдама тәсіл бойынша анықталған заңдылықтан ауытқу байқалуы мүмкін.

Р сенім ықтималдығының берілген дәрежесіне t критерийінің белгілі бір анықталған мәні сәйкес келеді.

n>30 болғанда сенім ықтималдығының Р=99,7% дәрежесіне t=3 мәні, ал Р=95,5% дәрежесіне t=2 мәні сәйкес келеді. n<30 болғанда t шамасы сенім ықтималдығының дәрежесіне сәйкес а арнайы кесте бойынша анықталады. (Н.А.Плохинского).

ҮЛГІ-ЕСЕП

Бақылау саны 30-дан үлкен болған жағдайда репрезентативтілік қатені () және бас жиынтықтың орта шамасының (_бас) сенім шекараларын анықтауға арналған .

Есептің шарты: адам ағзасына шу мен төмен жиілікті дірілдің құрамдасқан әсерін зерттеу барысында тексерілген ауылшаруашылығы көліктерінің 36 жүргізушісінің 1 сағ. жұмыс істегеннен кейінгі тамыр соғу жиіліктерінің орташа мәні минутына 80 соққы, σ= ±6 мин/соққы болғаны тағайындалды.

---

Тапсырма: репрезентативтілік қатені () және бас жиынтықтың орта шамасының (_бас) сенім шекараларын анықтау керек.

ШЕШУІ

1. Орта шаманың орта қатесін есептеу():

мин./соққы.

2. Бас жиынтықтың орта шамасының (_бас) сенім шекараларын есептеу.

Ол үшін:

а)сенім ықтималдығының дәрежесін беру: Р=95,5%;

б) t критерийінің шамасын анықтау: t=2.

Онда _бас=_таң±t = 80±2*1=80 ± 2 мин./соққы.

Қорытынды: 95,5% сенім ықтималдығымен тағайындалды: бас жиынтықтағы, яғни ауылшаруашылығы көліктерінің барлық жүргізушілерінің 1 сағ. жұмыс істегеннен кейінгі тамыр соғу жиіліктерінің орташа мәні 78 минутына соққыдан 82 минутына соққыға дейінгі аралықта болады, яғни тамыр соғу жиіліктерінің орташа мәні 78 минутына соққыдан кем, 82 минутына соққыдан жоғары болу мүмкіндігі кездесетін жағдайлар саны бас жиынтықта 5%-тен аспайды.

ҮЛГІ-ЕСЕП

репрезентативтілік қатені (m) және бас жиынтықтың салыстырмалы көрсеткішінің (Рбас ) сенім шекараларын анықтауға арналған.

Есептің шарты:Н қаласының аудандарының бірінде тұратын 3 жастағы 164 баланы медициналық тексеруден өткізгенде 18% жағдайда мүсіннің функционалдық сипатта бұзылуы табылды.

Тапсырма: : репрезентативтілік қатені (mР) және бас жиынтықтың салыстырмалы көрсеткішінің (Рбас) сенім шекараларын анықтау керек.

ШЕШУІ

1. Салыстырмалы көрсеткіштің репрезентативтілік қатесін есептеу:

2. Бас жиынтықтың салыстырмалы көрсеткіштерінің сенім шекараларын есептеу:

а) сенім ықтималдығының дәрежесін беру қажет (Р =95%);

б) берілген ықтималдық дәрежесі және 30- дан үлкен бақылаулар санына сәйкес t критерийінің шамасы 2-ге тең (t = 2).

Онда Рбас=Рт ±t = 18% ± 2*3 = 18% ± 6%.

Қорытынды: Р=95% сенім ықтималдығымен Н. қаласында тұратын 3 жасар балалардың мүсіннің функционалдық сипатта бұзылуының жиілігі 100 балаға шаққанда 12%-тен 24% аралығында болатындығы тағайындалды.

Қалыпты таралудың негізгі сипаттамалары:

• Сандық сипаттамалардың теңдігі (орта мән, мода және медиана өз ара тең);

• орта мәннен ауытқудың симметриялылығы;

• қисық астындағы жалпы аудан 1 ге тең;

• қисықтың ұштары екі бағытта да абцисса осіне үздіксіз жақындай отырып, алайда ешқашан онымен жанаспай шексіздікке ұмтылады.

• қисықтың түрі бас жиынтықтың орта квадраттық ауытқуымен анықталады;

• орта квадраттық ауытқуы аз таралуға жіңішке, жоғары созылған қисықтар, ал орта квадраттық ауытқуы үлкен таралуға жазыңқы қисықтар сәйкес келеді.

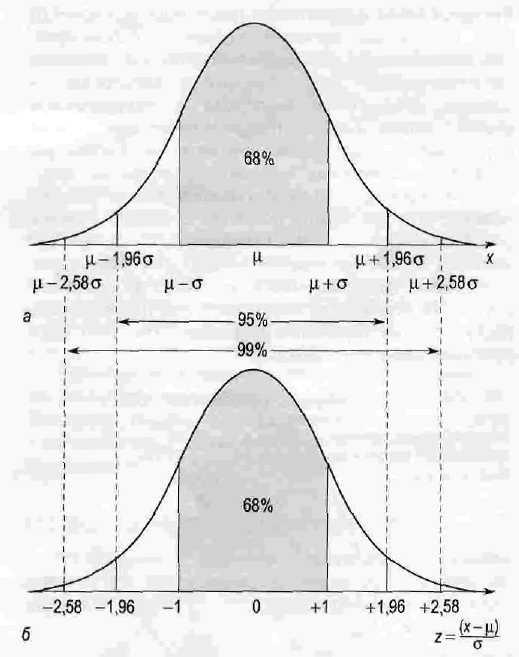
3 сигма ережесі.

барлық мәндердің 68,26% -і ±σ аралығында жатады (орта мәннен ±1 орта квадраттық ауытқу);

барлық мәндердің 95,44% -і ±2σ аралығында жатады ( орта мәннен ±2 орта квадраттық ауытқулар);

барлық мәндердің 99,73% -і ±3σ аралығында жатады (орта мәннен ±3 орта квадраттық ауытқулар).

Гаусс қисығы

Қалыпты таралу тығыздығының графигін қалыпты қисық немесе Гаусс қисығы деп атайды.

Қалыпты таралудың қисығы центрге қатысты симметриялы, қоңырау тәрізді түрі бар

---

3 сигма ережесі.

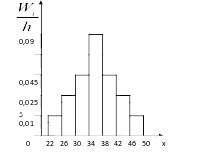
Мысал. Өте үлкен ампулалар партиясынан көлемі 50 болатын кездейсоқ таңдама алынды. Х белгісі – 1 см-ге дейінгі дәлдікпен өлшенген ампулалардың ұзындығы келесі вариациялық қатар түрінде берілген: 22, 24, 26, 26, 27, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Таралудың статистикалық дискретті, интервалдық қатарларын, мода, медиана, таңдама ортасын, дисперсияны, орта квадраттық ауытқу, сенімділік интервалын табу керек және тең қадаммен жиілік және салыстырмалы жиілік гистограммасын тұрғызу керек. Таңдаманың қалыпты таралу заңына бағынатындығын немесе бағынбайтындығын тексеру керек (3 сигма ережесінің орындалуы).

Шешімі. Таңдаманың дискретті статистикалық таралуы

	22	24	26	27	28	31	32	33	34	35	36	37	38	40	41	43	44	45	47	50
	1	1	2	1	2	3	2	4	5	2	5	6	2	5	2	1	2	2	1	1
	0,02	0,02	0,04	0,02	0,04	0,06	0,04	0,08	0,1	0,04	0,1	0,12	0,04	0,1	0,04	0,02	0,04	0,04	0,02	0,02

Мода М₀=37.

Медиана

Таңдама орта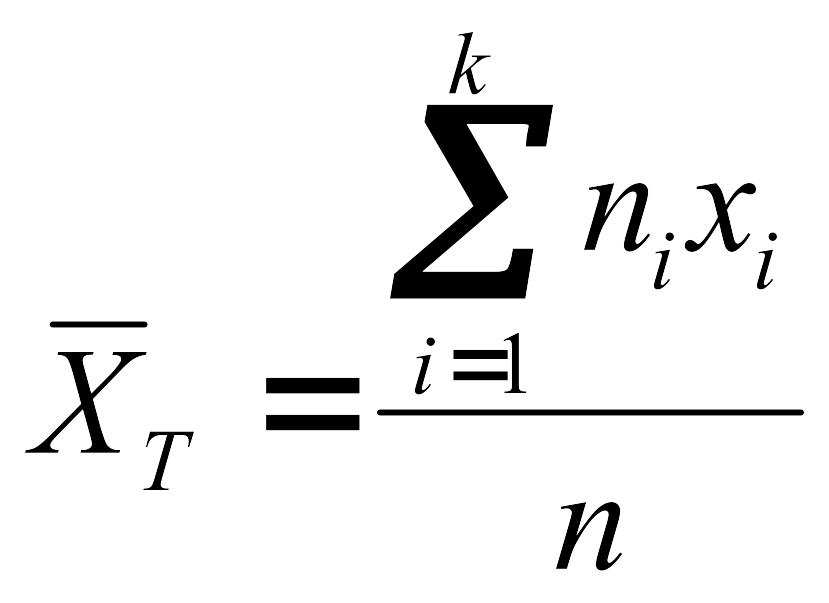

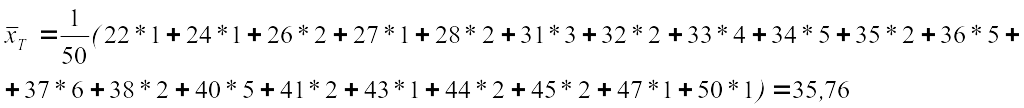
Таңдама дисперсия

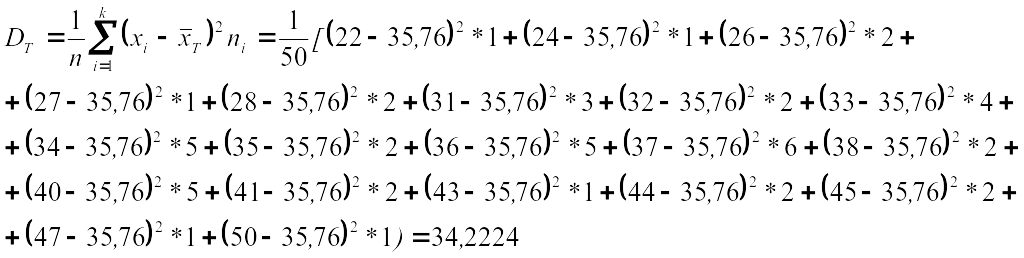
Таңдама орта квадраттық ауытқу деп таңдама дисперсиядан алынған квадрат түбірді айтады: .

Таңдама ортаның стандартты қатесі:

Бас орта және сенім интервалының арасында жатады.

Таңдаманың интервалдық статистикалық таралуы

екен, h табамыз

. Яғни,

Топтастыру интервалы
жиіліктер	2	5	9	18	9	5	2
салыстырмалы жиіліктер	0,04	0,1	0,18	0,36	0,18	0,1	0,04

Ж

0,5

1,25

2,25

4,5

0

22

26

30

34

38

42

46

50

x

иіліктер гистограммасы

Салыстырмалы жиіліктер гистограммасы

0,04

0,1

0,18

0,36

0

22

26

30

34

38

42

46

50

x

3 сигма ережесі.

• барлық мәндердің 68,26% ±σ аралығында жатады (орта мәннен ±1 орта квадраттық ауытқу);

• барлық мәндердің 95,44% ±2σ аралығында жатады (орта мәннен ±2 орта квадраттық ауытқулар);

• барлық мәндердің 99,73% ±3σ аралығында жатады (орта мәннен ±3 орта квадраттық ауытқулар).

,

,

.

Алынған деректерге сәйкес таңдама қалыпты таралған деп қорытынды жасауға болады.

Тапсырмалар.

1. Екі жастағы 20 ұл балалардың бойының ұзындығы: 92, 91, 90, 93, 91, 93, 91, 92, 90, 91, 95, 94, 92, 92, 92, 90, 95, 93, 94, 89 ( см ) тең. Таралудың статистикалық дискретті, интервалдық қатарларын, мода, медиана, таңдама ортасын, дисперсияны, орта квадраттық ауытқу, сенімділік интервалын табу керек және тең қадаммен салыстырмалы жиілік гистограммасын тұрғызу керек. Таңдаманың қалыпты таралу заңына бағынатындығын немесе бағынбайтындығын тексеру керек (3 сигма ережесінің орындалуы).

2. Ауылдық мекендер үшін 25 жас шамасындағы ер адамдардың бойлары қарастырылды. Көлемі 35 кездейсоқ таңдама бойынша: 175, 167, 168, 169, 168, 170, 174, 173, 177, 172, 174, 167, 173, 172, 171, 171, 170, 167, 174, 177, 171, 172, 173, 169, 171, 173, 173, 168, 173, 172, 166, 164, 168, 172, 174. Таралудың статистикалық дискретті, интервалдық қатарларын, мода, медиана, таңдама ортасын, дисперсияны, орта квадраттық ауытқу, сенімділік интервалын табу керек және тең қадаммен салыстырмалы жиілік гистограммасын тұрғызу керек. Таңдаманың қалыпты таралу заңына бағынатындығын немесе бағынбайтындығын тексеру керек (3 сигма ережесінің орындалуы).

---

3. Фармацевтикалық фабрикадан шығарылатын өнімдерден кездейсоқ жағдайда гомеоетикалық препараттардың 15 жәшігі таңдап алынды. Олардағы таблеткалардың саны сәйкесінше 50, 51, 48, 52, 50, 49, 50, 47, 50, 51, 49, 50, 52, 48, 49 – ге тең. Таралудың статистикалық дискретті, интервалдық қатарларын, мода, медиана, таңдама ортасын, дисперсияны, орта квадраттық ауытқу, сенімділік интервалын табу керек және тең қадаммен салыстырмалы жиілік гистограммасын тұрғызу керек. Таңдаманың қалыпты таралу заңына бағынатындығын немесе бағынбайтындығын тексеру керек (3 сигма ережесінің орындалуы).

4. Кездейсоқ жағдайда таңдалынған 30 науқастың артериалды қысымдарын өлшегенде келесі нәтижелер алынды: 151, 166, 133, 155, 179, 148, 143, 128, 138, 172, 168, 157, 158, 136, 169, 153, 142, 147, 134, 164, 167, 131, 152, 147, 176, 122, 149, 154, 161, 156. Таралудың статистикалық дискретті, интервалдық қатарларын, мода, медиана, таңдама ортасын, дисперсияны, орта квадраттық ауытқу, сенімділік интервалын табу керек және тең қадаммен салыстырмалы жиілік гистограммасын тұрғызу керек. Таңдаманың қалыпты таралу заңына бағынатындығын немесе бағынбайтындығын тексеру керек (3 сигма ережесінің орындалуы).

---

Смотрите также файлы

• 1-beyorganika.docx

• ГИПОКСИЯ ВНУТРИУТРОБНОГО ПЛОДА И АСФИКСИЯ НОВОРОЖДЕННЫХ.doc

• - СРС 2нов-ОМ- 14-15.doc

• +Тест.docx

• ТЕРАПИЯЛЫҚ СТОМАТОЛОГИЯ ПРОПЕДЕВТИКАСЫ МОДУЛІ.doc