Алгоритмы и структуры данных

Практическая работа № 7. Разработка и применение циклического списка. Задача Иосифа.

Циклический списокНа практике нередко возникают задачи, при которых требуется последовательный просмотр данных по «кругу», когда последний элемент замкнут на первый или наоборот, первый – на последний. Например, операция поиска и замены элементов текста в текстовых файлах современных редакторах. Такие операции реализуются с помощью специальных линейных структур, называемых кольцевыми (циклическими) списками. Кольцевой список — это список, у которого последний элемент связан с первым. 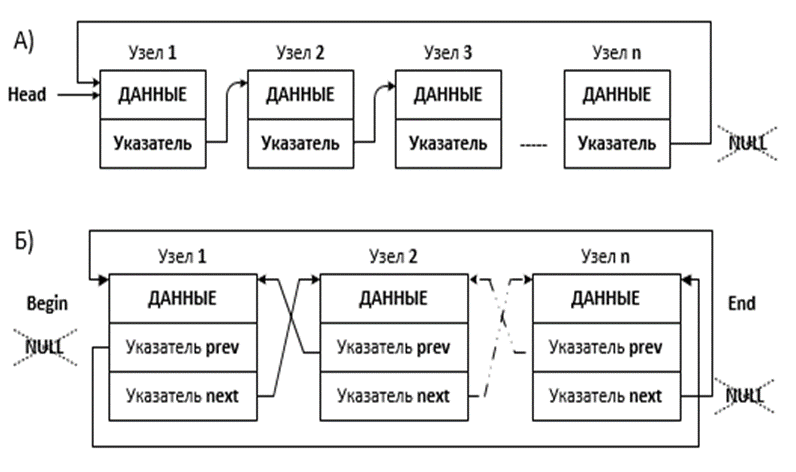Кольцевой список можно сделать как односвязным, так и двухсвязнымЯсно, что эти типы данных являются абстракциями линейного односвязного и двусвязного списков. Отличие состоит лишь в том, что при инициализации кольцевых списков – в односвязном линейном списке указатель next последнего элемента устанавливается не в NULL, а замыкается на первый элемент; в двусвязном списке – еще и указатель prev первого элемента устанавливается на последний элемент. При выполнении операций обхода нужно «отслеживать» признаки первого или последнего элемента. Рассмотрим эти особенности на примере линейного односвязного кольцевого списка. Для представления его узлов используют те же две структуры.

---

Для представления данныхstruct Data {int a; }; Для представления узлов (Node) спискаstruct Node{ Data d; // поле для данных типа DataNode *next; // поле указателя next на следующий элемент такого же узла};При инициализации в функции Init_Circle_1() корневого узла, его указатель next «замыкается» сам на себя.Node * Init_Circle_1(int h) // h- значение первого узла{Node *p;p = new Node; // выделение памяти под корень спискаp->d.a = h; // сохранение данныхp->next = p; // указатель на корневой узелreturn(p);}Ввод узлов циклического списка реализуется функцией Insert_Circle_1() в которой у каждого нового узла (new_node), его указатель next устанавливается на корневой узел.Node * Insert_Circle_1(Node *x, int h){Node *new_node, *p;p = x->next; // сохранение указателя узла на следующий узел new_node = new Node;new_node->d.a = h; // сохранение поля данных добавляемого узлаx->next = new_node; // предыдущий узел указывает на новыйnew_node->next = p; // созданный узел указывает на корневой узел return(new_node);} В функции Print_Circle_1() единственным отличием от функции печати односвязного списка, или от функции обхода двусвязного списка в прямом порядке является условие окончания цикла p!=x (пока не найден корень) – вместо p!=NULL (пока не найден признак конца списка).void Print_Circle_1(Node *x){ Node *p = x;do{ cout<<p->d.a<<" "; // вывод значения элемента узла p p = p->next; // переход к следующему узлу} while (p != x); // условие окончания обхода}Задача Иосифа.Пожалуй все в далеком детстве играли в прятки или в пятнашки и помнят считалки с помощью которых определяли первого игрока, которому приходилось «водить». По сути дела считалка и являлась модифици-рованной задачей Иосифа. В считалке, счет идет от первого слова до последнего. В задаче Иосифа от единицы до любого числа, меньшего общего количества людей при этом выбывает человек, номер которого совпадет с этим числом, и расчет продолжается циклически до того момента, когда останется один человек.

---

Если общее число людей равно , а счет проводится до 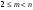, то на каждом шаге выбывающий имеет порядковый номер , а дальше счет начинается с 1 (со следующего участника), продолжается до и т.д. до того момента, когда останется всего один участник. Для решения задачи на компьютере удобным аппаратом является моделирование решения задачи с помощью линейного списка, конкретно — циклического односвязного списка. Так же, как и в обычном односвязном списке, удаление узлов циклического списка возможно по значению данных, номеру узла или его адреса. В циклическом списке указатель next замкнут на корень. Поэтому особенностью операции удаления узла циклического списка является то, что все другие узлы, начиная со следующего после удаленного, сдвигаются «влево», и сам следующий узел становится корнем списка. Например, если начальный список u0 = {1, 2, 3, 4, 5, 6, 7, 8, 9}, то после удаления элемента с номером, например, 5, новым списком будет список u1 = {6, 7, 8, 9, 1, 2, 3, 4}. Функция Del_Node_Circle_1() на вход получает указатель на корень списка и номер узла, который нужно удалить. Если номер узла не совпал с искомым, то узел пропускается и поиск начинается со следующего узла (цикл for()). При нахождении узла p с искомым номером, указатель next узла предшественника (ptr->next) устанавливается на следующий за p узел (ptr->next=p->next), после чего узел p удаляется (delete(p)). Функция возвращает в точку вызова указатель на новый список (return x).Node* Del_Node_Circle_1(Node* x, int N){if (x != NULL){ Node *p = x;if (x->next != x) // если узел не последний{ for (int i = 1; i < N; i++) // поискаузла p->next сискомымномеромp = p->next;Node *ptr = x;while (ptr->next != p) // указатели всех узлов перенастраиваем на узел pptr = ptr->next;// удаление узла p

---

ptr->next = p->next;if (x = p)x = p->next;delete(p);}return x;}Операция удаления кольцевого списка хорошо иллюстрируется как раз на классическом примере решения задачи Иосифа («выбор лидера»). Еще раз напомним ее условие. В круг становится k человек на позицию с соответствующим номером. На каждом шаге просмотра круга из него удаляется человек, позиция которого при просмотре равна n. Круг смыкается и поиск следующего человека с номером позиции n в новом круге продолжается. 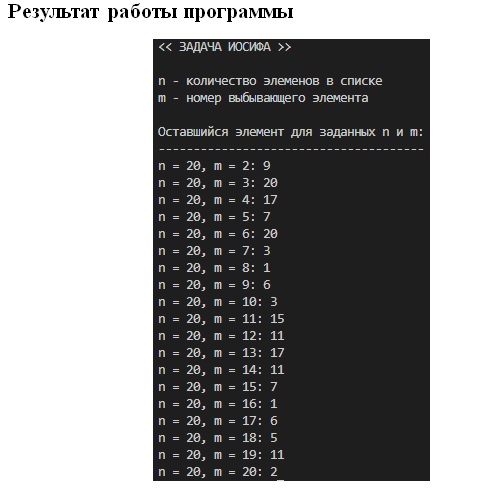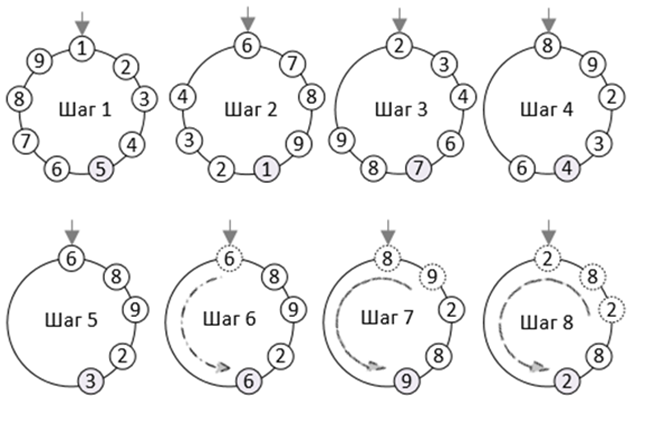Определить, кто (человек с первоначальным номером позиции) останется не удаленным.Ниже представлена схема шагов решения задачи для k=9 и n=5 (удаление каждого пятого). Далее представлен результат работы программы решения задачи. Этот результат можно получить, доработав интерфейс вызова функции Del_Node_Circle_1() в точке ее вызова. Например, через цикл вызова, условием окончания которого является признак того, что в списке остался единственный узел:while(u->next!=u){u= Del_Node_Circle_1(u, n);Print_Circle_1(u);}Схема решения задачи ИосифаиКонечный результат циклического вызова функции Del_Node_Circle_1().Задание.Пусть общее число участников 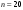, а расчет производится от 2 и до 20. На экран монитора требуется вывести 19 результатов расчета, т.е. фиксированное число и при каждом расчете равно 20, а меняется от 2 при первом до 20 при последнем расчете.

---

Смотрите также файлы

• Дорожная карта мероприятий по обеспечению перехода на новые фгос ноо, фгос ооо на 20212027 годы.docx

• Занятие Психосоматические состояния. Механизмы психосоматических состояний. Внутренняя картина болезни.docx

• Обзор рынка недвижимости. Анализ рынка объекта оценки, ценообразующих факторов, а также внешних факторов, влияющих на его стоимость.docx

• Тестовые задания по общей микробиологии.pdf

• Один день в Мемфисе.docx