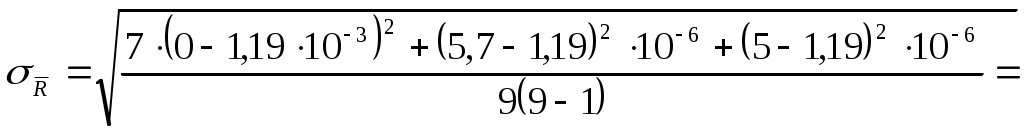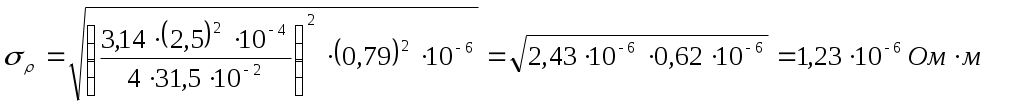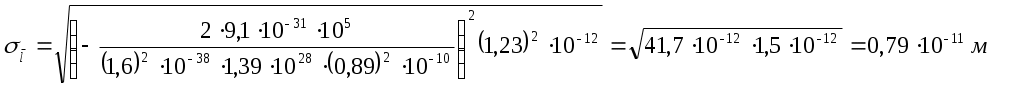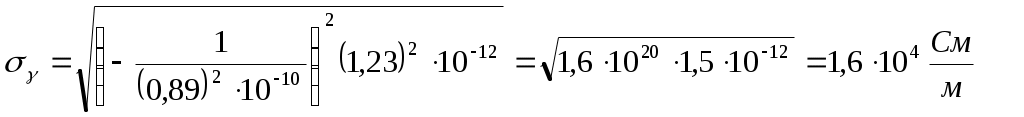Федеральное агентство по образованию Российской ФедерацииГосударственное образовательное учреждение высшего профессионального обученияНациональный минерально-сырьевой университет «Горный»Кафедра общей и технической физикиЛабораторная работа №6

Тема: Измерение низких сопротивлений материалов.

^{(подпись) (Ф.И.О.)}

Проверил: доцент ____________ Левин К. Л.

^{(должность) (подпись) (Ф.И.О.)}Санкт-Петербург2016Цель работы: определить удельное сопротивление металлов и других низкоомных материалов с помощью измерительного усилителя.Краткое теоретическое обоснование.Электрическое сопротивление – величина, характеризующая сопротивление проводника электрическому току. Зависит от размеров и формы проводника.1 Ом – сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток 1 А.Удельное сопротивление – сопротивление проводника длиной 1 м и площадью поперечного сечения 1 мм². Зависит от свойств материалаСпособность вещества проводить электрический ток характеризуется его удельным сопротивлением , либо удельной проводимостью . Их величина определяется химической природой вещества и условиями, в частности температурой, при которых оно находится.1 См (сименс) – проводимость участка электрической цепи сопротивлением 1 Ом.Классическая электронная теория проводимости металлов:

1. 
   Закон Джоуля – Ленца.
   

Дополнительная энергия, приобретаемая электроном к концу свободного пробега

---

, идет на нагревание металла.



Число столкновений электрона за 1с с узлами решетки . Если n – концентрация электронов, то энергия, передаваемая решетке в единице объема в единицу времени,

2. 
   Закон Видемана – Франца.
   

Отношение теплопроводности к удельной проводимости для всех металлов при одной и той же температуре одинаково и увеличивается пропорционально температуре: , где .Классическая теория объяснила законы Ома и Джоуля – Ленца и качественно объяснила закон Видемана – Франца.Длина свободного пробега электронов в проводниках – путь, который в среднем проходят электроны между двумя последовательными столкновениями с ионами решетки. 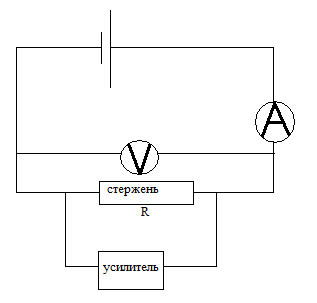В конце свободного пробега скорость электрона равна нулю, так как электрон отдает всю энергию ионам решетки.Свободные электроны – электроны, движение которых подчиняется законам классической статики.Схема установки:Расчетные формулы: сопротивления проводников на основании закона ОмаS = d²/4 удельное сопротивлениеR_к = R_п  – Rконтактное сопротивление R_к концентрация свободных электронов удельная электропроводность по классической теории, где

---

– средняя скорость теплового движения, - средняя длина свободного пробега электронов.

удельная электропроводность по квантовой теории, где  – удельное сопротивление, n – концентрация электронов, – их средняя длина свободного пробега, h– постоянная Планка.
Формулы погрешности:










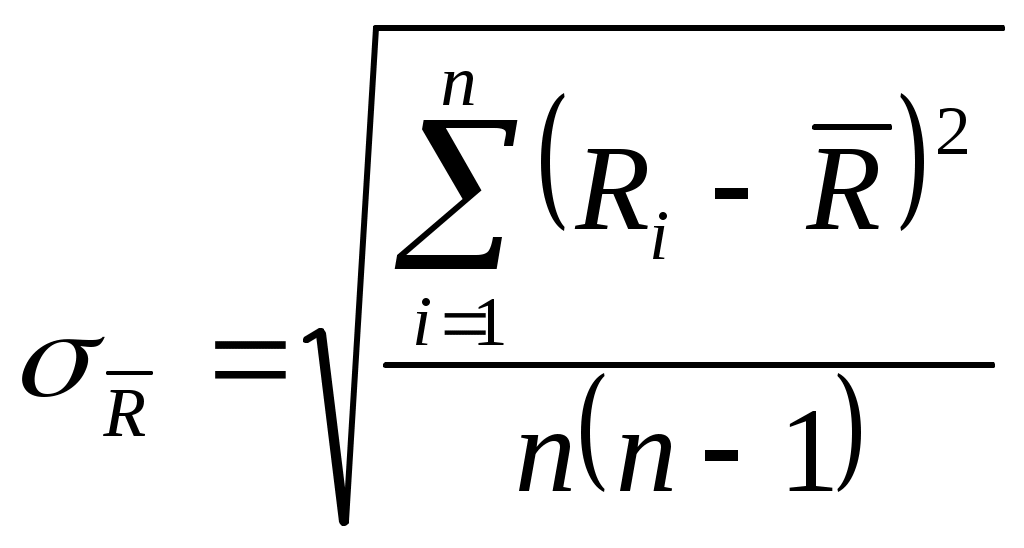
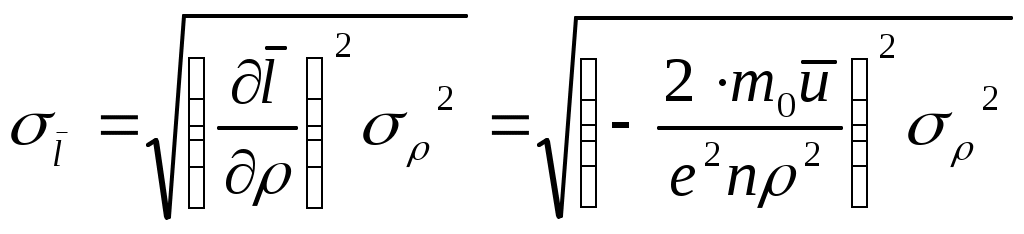
Ход работы:
Вольт – амперная характеристика алюминиевого стержня.

Табл.1

I	А	0	0,25	0,50	0,75	1,00	1,25	1,50	1,75	2,00
U	В	0	0,002	0,006	0,009	0,017	0,023	0,03	0,033	0,038
RAl	Ом	0	0,00008	0,000012	0,000012	0,000017	0,000018	0,000018	0,000018	0,000019

Измерение полного сопротивления R_п (с учётом контактного сопротивления R_к Al)Табл.2

I	А	0	0,25	0,50	0,75	1,00	1,25	1,50	1,75	2,00
U	В	0	0,44	0,89	1,32	1,74	2,18	2,61	3,04	3,47
Rп	Ом	0	1,76	1,78	1,76	1,74	1,744	1,74	1,737	1,735
Rк Al	Ом	0	1,76	1,78	1,76	1,74	1,736	1,733	1,726	1,725

---

Вольт – амперная характеристика медного стержня.Табл.3

I	А	0	0,25	0,50	0,75	1,00	1,25	1,50	1,75	2,00
U	В	0	0,008	0,01	0,011	0,022	0,028	0,03	0,035	0,039
RCu	Ом	0	0,00003	0,00002	0,000024	0,000032	0,00003	0,00003	0,00003	0,000026

Измерение полного сопротивления R_п (с учётом контактного сопротивления R_к Cu)Табл.4

I	А	0	0,25	0,50	0,75	1,00	1,25	1,50	1,75	2,00
U	В	0	0,49	0,95	1,45	2,08	2,47	2,85	3,28	3,81
Rп	Ом	0	1,96	1,9	1,93	2,08	1,976	1,9	1,874	1,905
Rк Cu	Ом	0	1,96	1,9	1,93	2,08	1,976	1,9	1,8683	1,9

Обработка результатов:d = 2,5 см l = 31,5 смпри Т=300 К м/c Кл кгd_Al=2700 кг/м³

---

(плотность алюминия)

d_Cu=8920 кг/м³ (плотность меди)
Алюминиевый стержень.














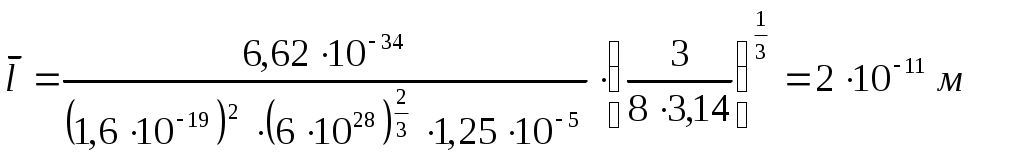
Расчет погрешностей.











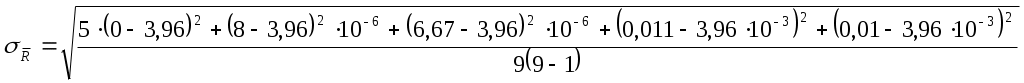
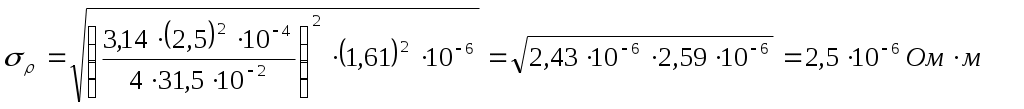
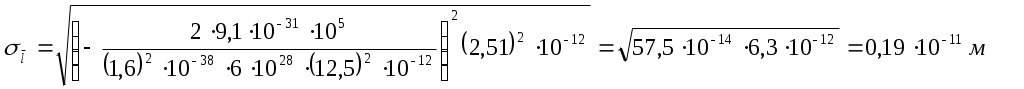
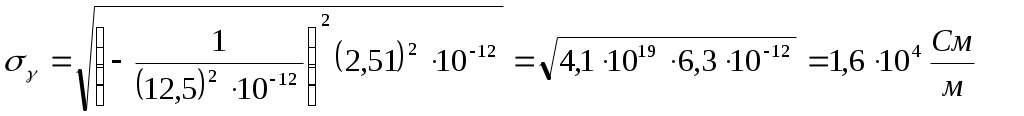
Медный стержень.





Ом








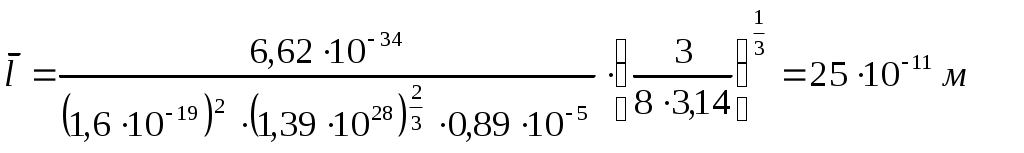
Расчет погрешностей.

---

Смотрите также файлы

• Минобрнауки россии федеральное государственное бюджетное образовательное учреждение высшего образования Ухтинский государственный технический университет.docx

• Составить обзор научных и педагогических идей (трудов) и проанализировать как менялась педагогическая мысль за всю историю человечества.docx

• Программа среднего профессионального образования 46. 02. 01 Документационное обеспечение управления и архивоведение Дисциплина Экономика. Индивидуальный проект.docx

• Контрольная работа 1 по теме Первоначальные химические понятия.docx

• Русский язык и культура речи Какой принцип является главной коммуникативной нормой, определяющей весь процесс коммуникации.docx