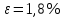Лабораторная работа (вариант 34)

Определение ускорения свободного падения с помощью

математического маятника

Цель работы: определение ускорения свободного падения 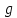при помощи математического маятника, изучение погрешностей измерений физических величин и применение на практике для оценки точности определения .

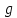Приборы и принадлежности: электронный тренажер, лабораторная установка «Математический маятник», секундомер, рулетка.
Теоретическая часть

Математическим маятником (рис.1) называется материальная точка на конце легкой нерастяжимой нити или невесомого стержня.



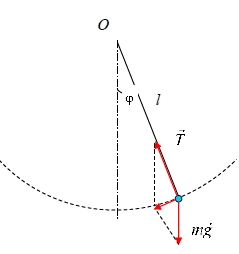
Рис.1 Математический маятник

Здесь m – масса материальной точки, l – длина нити, 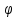- угол отклонения нити от вертикали.

Колебания – это движения или процессы, обладающие той или иной степенью повторяемости во времени.

Периодическим называется такое колебание, у которого каждый цикл в точности воспроизводит любой другой цикл. У всякой системы, способной совершать свободные колебания, имеется устойчивое положение равновесия.

Гармонические колебаниями (Рис.2) физической величины 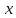называется процесс измерения ее во времени 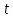по закону: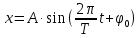



где 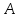- амплитуда колебаний, 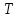- период колебаний,

Величина 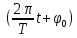называется фаза колебаний,

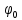- начальная фаза колебаний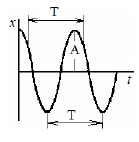

---

Рис.2 График гармонических колебаний

Амплитудой называется максимальное значение колеблющейся величины.

Частотой ν называется количество колебаний, совершаемых в единицу времени.

Периодом колебания называется время, за которое совершается одно полное колебание (цикл).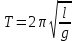



ν – величина, обратная периоду колебаний: ν = 1/Т.

ω – циклическая частота колебаний:

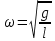
Для определения ускорения свободного падения :


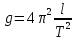
Описание экспериментальной установки

Схема экспериментальной установки и входящие в неё приборы и принадлежности приведены на рис.3.



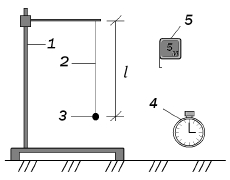
Рис.3 Экспериментальная установка

1. 
   штатив; 2 – длина маятника; 3 – шарик; 4 – секундомер; 5 – рулетка
   

Если измерить расстояние от точки подвеса до центра тяжести шарика l, вывести из положения равновесия шарик, отклоняя его на угол 5–7°, при помощи секундомера определить время t некоторого числа n полных колебаний, затем найти период 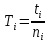, то ускорение свободного падения можно определить по формуле 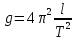. При работе с математическим маятником имеется возможность изменять длину нити l и число колебаний n. Следует иметь в виду: при увеличении длины маятника и числа колебаний уменьшается экспериментальная погрешность.

Рабочие формулы:

1. 
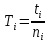   – период колебаний
   
2. 
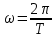   - циклическая частота колебаний
   
3. 
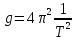   – определение ускорения свободного падения
   
4. 
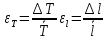   - случайная погрешность измерений периода колебаний и длины маятника
   
5. 
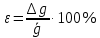   - относительная погрешность ускорения свободного падения
   

---

Экспериментальная часть

1.Установим заданную длину 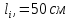. Отклоним шарик приблизительно на 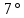от положения равновесия и отпустим. Измерим секундомером время 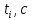, с периодами полных колебаний числа 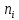. Выполним необходимые измерения и вычисления и запишем в таблицу 1.

Таблица 1. Измерения и вычисления

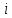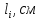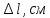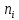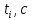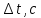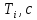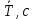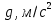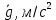1	50	0,5	07	9,906	0,001	1,415	1,413	9,85	9,88
2	50		08	11,247		1,406		9,98
3	50		09	12,745		1,416		9,83
4	50		10	14,112		1,411		9,90
5	50		11	15,608		1,419		9,79

2. Найдем период колебаний

---

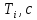
по формуле . Результат запишем в таблицу 1.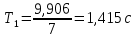











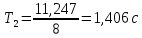
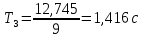
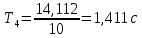
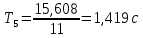
3. Вычислим среднее арифметическое периода колебаний :





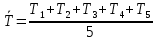
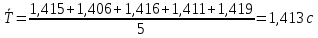
4. Определим ускорение свободного падения для каждого измерения по формуле:













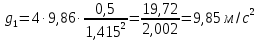
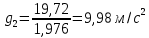
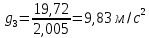
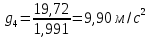
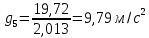
5. Вычислим ускорение свободного падения, подставляя среднее значение длины маятника 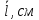и периода :



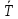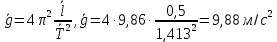
6. Найдем абсолютную погрешность ускорения свободного падения. Для определения случайной погрешности измерений периода колебаний составим таблицу 2, в которую занесём результаты измерений, промежуточные вычисления и другие необходимые данные для подстановки их в формулу.

Таблица 2. Вычисления

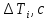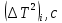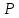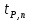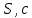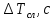1	1,415	-0,002	0,000004	1,413	0,95	2,78	0,002	0,005
2	1,406	0,007	0,000049
3	1,416	-0,003	0,000009
4	1,411	0,002	0,000004
5	1,419	-0,006	0,000036

---

1. 
   
   
2. 
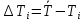
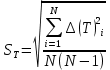   , где 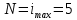- число опытов,
   

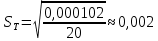
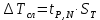, где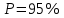 - доверительная вероятность, , ,

3. 
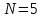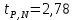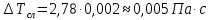
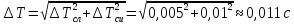
   случайная погрешность измерений периода колебаний и длины маятника:
   

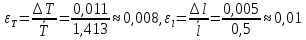
Вычисления показали, что погрешност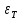и и 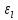– одного порядка, поэтому подставим полученные значения относительных погрешностей измерения длины и периода колебаний маятника в формулу: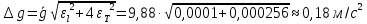



Получили численное значение абсолютной погрешности измерения ускорения свободного падения .

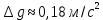Относительная погрешность ускорения свободного падения:



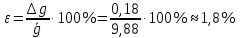
7. Запишем окончательный результат определения ускорения свободного падения с учётом границ доверительного интервала :

,

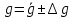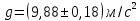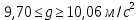
Табличное значение величины 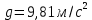попадает в полученный доверительный интервал.

Вывод: В результате проведенного лабораторного эксперимента определено ускорение свободного падения 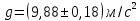с надёжностью 95 % при числе измерений n = 5 и относительной погрешности

---

Смотрите также файлы

• Причины травм.docx

• Практическая работа 1 Работа с файлами с использованием файлового менеджера Тип урока изучение нового материала Цели урока.doc

• Задания Рассмотрите пример и укажите вид информации.doc

• Задание 1 Построение модели Черный ящик Порядок выполнения работы.docx

• Задания 2 Построение модели состава системы Порядок выполнения работы.docx