3.5. Аппроксимация функции полиномами, коэффициенты которых определены по методу наименьших квадратов (МНК)

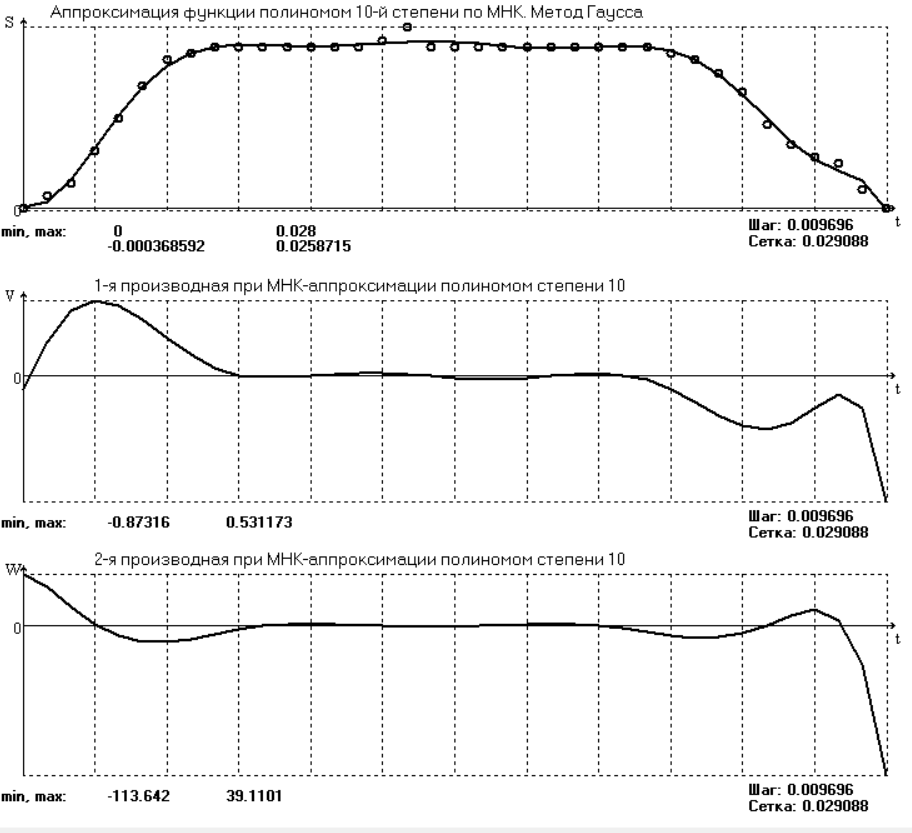
По этому методу искомую гладкую функцию строят в виде суммы простых аналитических функций, выбор которых является отдельной не тривиальной задачей. В данной программе используется самая простая – система степенных функций: 1, t, t 2 , t 3 , … , так, что нужная гладкая функция получается в виде полинома: SП(t) = b0 + b1t + b2t 2 + b3t 3 + … + bnt m , (3.5) где m – задаваемая пользователем степень полинома. Таким образом, задача сводится к нахождению оптимальной степени полинома m и коэффициентов bi таких, чтобы график SП(t), получаемый по формуле (3.5), проходил между точками исходной функции, минимизируя среднеквадратическое отклонение значений исходной функции от значений полинома (3.5). Исследования, проведённые с помощью программы ApproxFSP, показали, что наилучшие результаты получаются для степени полинома m = 16. При этом решать систему уравнений при определении коэффициентов bi следует с помощью обращения матрицы системы. На рис. 3.8 показаны результаты аппроксимации. Функция аппроксимирована удовлетворительно на фазах удаления и возврата, но неудовлетворительно на фазах ближнего и дальнего выстоя. Данный вариант аппроксимации следует признать неприемлемым, поэтому зависимости скорости и ускорения не приводим.





Вывод:

С помощью структурного анализа механизма мы определили: количество звеньев, количество и типы кинематических пар, наличия пассивных связей, вычисления чисел степеней свободы.

Мы определили кинематические параметры движения (перемещение, скорость, ускорение), связанные друг с другом как первообразные и производные функции. Функции скорости и ускорения мы

---

получили с помощью математической обработки

Функция аппроксимировалась пятью методами, четыре из которых позволяют сглаживать функции.

Сглаживание может быть необходимо, например, в тех случаях, когда функция искажена погрешностями эксперимента.

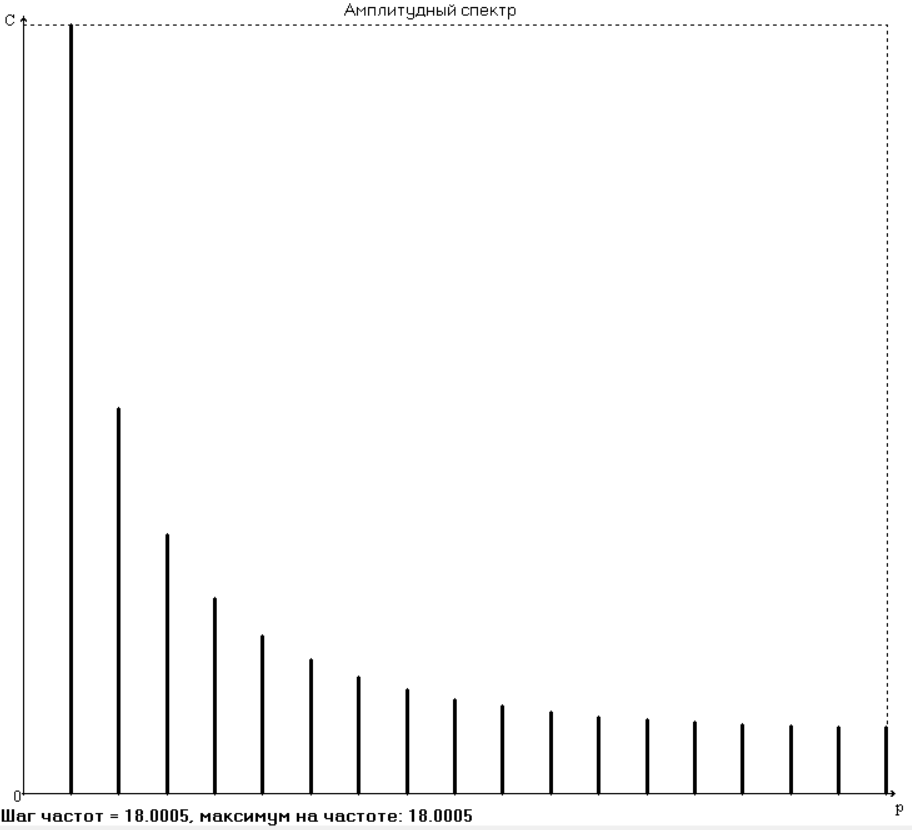
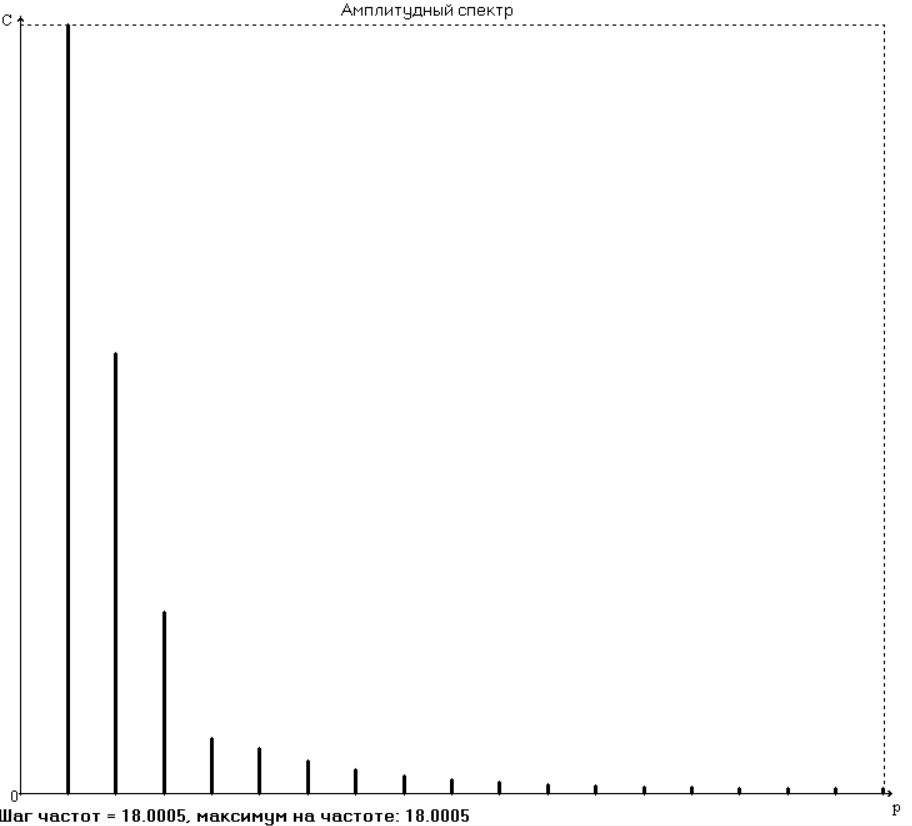
Ряд Фурье позволяет производить как интерполирующую, так и сглаживающую аппроксимацию. Для сглаживающей аппроксимации следует при разложении учитывать лишь первые основные частоты, что определяется по амплитудному спектру.

Тригонометрические ряды Фурье хорошо аппроксимируют гладкие периодические функции.

С помощью скользящих средних удовлетворительно выполнена сглаживающая аппроксимация самой функции, несколько хуже – первой производной и неудовлетворительно – второй производной.

Интерполяционные сплайны целесообразно применять в тех случаях, когда аппроксимирующую функцию надо проводить в точности по исходным точкам.

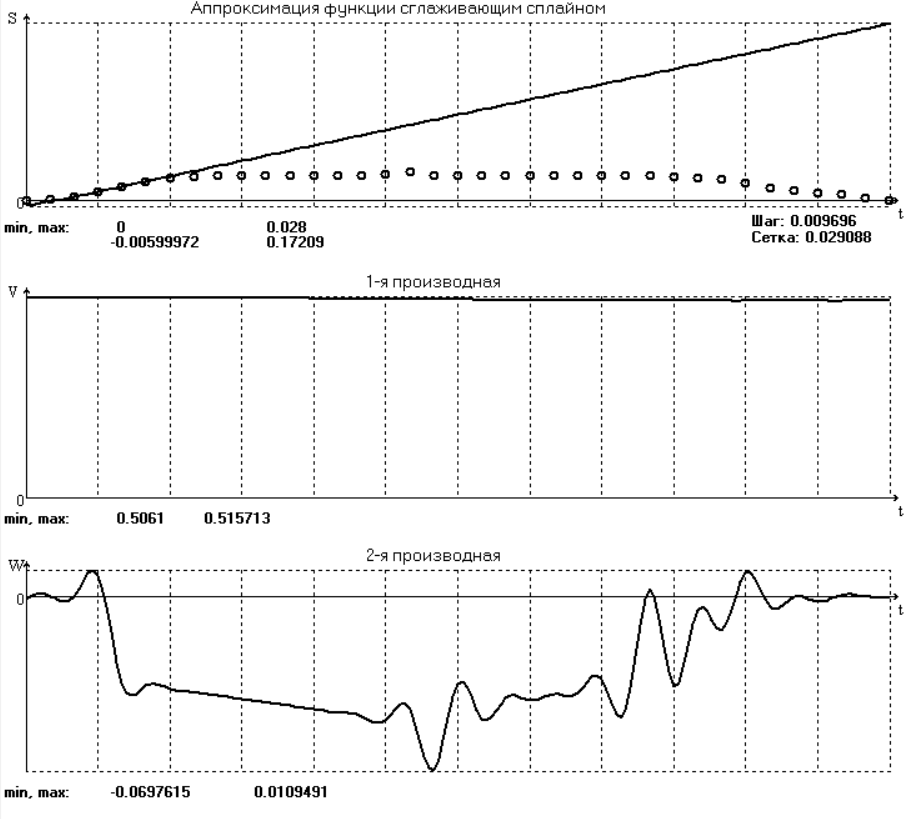
При использовании сглаживающего сплайна функция ушла от экспериментальных значений.

Литература

1. Лавров В.Ю. Введение в теорию механизмов и машин (ТММ): учебное

пособие / Балт. гос. техн. ун-т. СПб., 2016. 151 с.

2. Лавров В.Ю. Курсовое проектирование по теории машин и механизмов в

среде программы Mechanic: учебное пособие / Балт. гос. техн. ун-т. СПб., 2013. 32 с.

---

Смотрите также файлы

• Проверяемая цель.docx

• Лекция Учение о половом цикле. План лекции.pdf

• Тоо казахалтын филиал рудник жолымбет.docx

• Практическая работа к разделу 1 Ценности.docx

• Удк 34 doi 10. 34670AR. 2020. 32. 82. 001.pdf