Файл: 1. Проверить удовлетворяет ли функция заданному уравнению.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 21
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1.Проверить удовлетворяет ли функция заданному уравнению
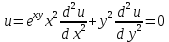
Найдем частные производные первого и второго подярка
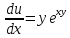
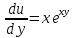
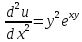
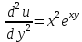
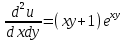
Подставим
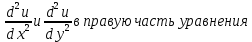
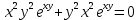
Проведем упрощения
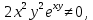
Следовательно функция не удовлетворяет заданному уравнению
2 Охарактеризовать точки безусловного экстремума и найти безусловные экстремумы следующих функций
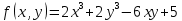
Найдем частные производные первого порядка
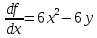
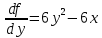
Решим систему уравнений
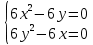
Находим критические точки функции
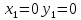
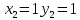
Найдем частные производные второго порядка
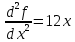
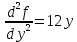
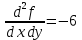
Вычисляем значения частных производных второго порядка в каждой из найденных критических точек
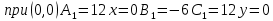
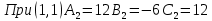
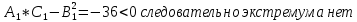
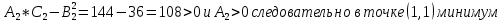
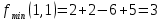
Ответ:
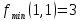
3 Охарактеризовать точки безусловного экстремума заданной функции.
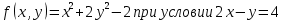
Найдем экстремум функции
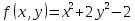, используя функцию ЛагранжаВ качестве целевой функции, подлежащей оптимизации, в этой задаче выступает функция:
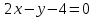
Составим вспомогательную функцию Лагранжа:
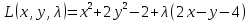
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным x,y и неопределенному множителю λ.
Решим систему уравнений
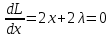
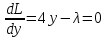
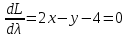
Решив данную систему, получаем стационарные точки
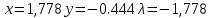
Определение типа экстремума в стационарных точках.
Для определения типа экстремума необходимо вычислить матрицу Гессе для точки M(1,778; -0,444; -1.7778), либо найти значения функции в каждой из точек и выбрать экстремальное.
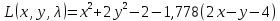
Найдем частные производные.
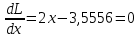
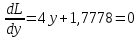
Решим систему уравнений и получим
Найдем частные производные второго порядка
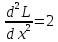
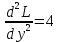
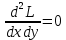
Вычислим значение этих частных производных второго порядка в стационарных точках
Вычисляем значения для точки (1,778; -0,444)
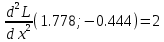
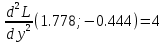
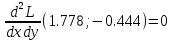
Строим матрицу Гессе:
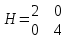
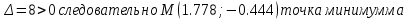
4 Методом Лагранжа найти и охарактеризовать точки локального условного экстремума
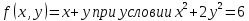
Найдем экстремум функции
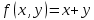, используя функцию ЛагранжаВ качестве целевой функции, подлежащей оптимизации, в этой задаче выступает функция:
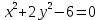
Составим вспомогательную функцию Лагранжа:
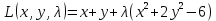
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным x,y и неопределенному множителю λ.
Решим систему уравнений
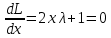
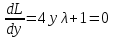
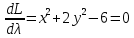
Решив данную систему, получаем стационарные точки
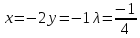
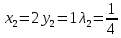
Определение типа экстремума в стационарных точках.
Для определения типа экстремума необходимо вычислить матрицу Гессе для точки M1(-2;-1;-1/4); M2(2;1;1/4) либо найти значения функции в каждой из точек и выбрать экстремальное.
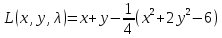
Найдем частные производные.
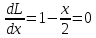
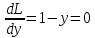
Решим систему уравнений и получим
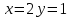
Найдем частные производные второго порядка
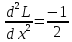
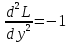
Вычислим значение этих частных производных второго порядка в стационарных точках
Вычисляем значения для точки (2;1)
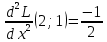
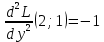
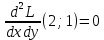
Строим матрицу Гессе:
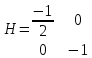
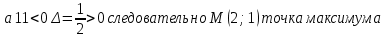
Для точки M2(2;1;1/4)
Найдем частные производные.
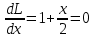
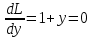
Решим систему уравнений и получим
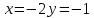
Вычислим значение этих частных производных второго порядка в стационарных точках
Вычисляем значения для точки (2;1)
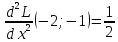
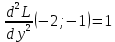
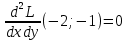
Строим матрицу Гессе:
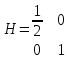
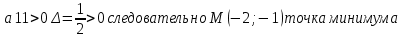
5. Найти наибольшее и наименьшее значение заданной функции в области D, ограниченной заданными графиками заданных функций
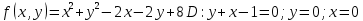
Составим вспомогательную функцию Лагранжа:
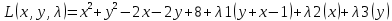
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным
x,y и неопределенному множителю λ.
Решим систему уравнений
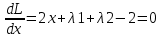
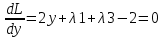
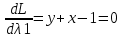
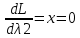
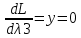
Данная система не имеет решений, следовательно точек минимума и максимума в указанной области нет.
6. Найти параметры линейной зависимости по данным таблицы методом наименьших квадратов и записать полученную линейную функцию
| x | -3.4 | -3.2 | -3.1 | -2.5 | -1.5 |
| y | -13,9 | -12,9 | -12.2 | -9.1 | -4.2 |
| | x | y | x^2 | y^2 | x*y | Y` |
| | -3,4 | -13,9 | 11,56 | 193,21 | 47,26 | -13,83 |
| | -3,2 | -12,9 | 10,24 | 166,41 | 41,28 | -12,81 |
| | -3,1 | -12,2 | 9,61 | 148,84 | 37,82 | -12,3 |
| | -2,5 | -9,1 | 6,25 | 82,81 | 22,75 | -9,24 |
| | -1,5 | -4,2 | 2,25 | 17,64 | 6,3 | -4,13 |
| сумма | -13,7 | -52,3 | 39,91 | 608,91 | 155,41 | |
| среднее | -2,74 | -10,46 | 7,982 | 121,782 | 31,082 | |