Файл: Вершинами графа, элементы множества e называются ребрами графа а пара (V, e ), т е. множество вершин и ребер графа называется графом. Если две вершины графа соединены ребром, то такие вершины называются смежными.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 77
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Теория графов
Пусть задано некоторое множествоVи множество E пар различных элементов из
V . Элементы этого множества V называются вершинами графа , элементы множества
E называются ребрами графа . а пара (V , E ) , т.е. множество вершин и ребер графа называется графом . Если две вершины графа соединены ребром , то такие вершины называются смежными . Вершины , которые соединены ребром называются его
Концами. Если вершина является концом ребра , то будем говорить , чторебро
выходит из вершины .Число ребер , выходящих из вершины vназывается степенью вершины и обозначается d(v) . Вершина степени 0 называется изолированной , степени 1висячей . Граф H называется подграфом графа G, если вершины и ребра H
принадлежат G .
Подграф H графа G называется подграфом , порожденным
множеством вершин {
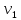 ,
, 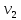 ,…,
,…,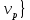 , если он содержит вершины
, если он содержит вершины 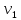 ,
, 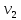 ,…,
,…,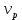 и
и все ребра графа G , соединяющие эти вершины .
Подграф H графа G называется подграфом , порожденным
множеством ребер {
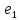 ,
, 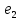 ,…,
,…,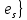 , если он содержит ребра
, если он содержит ребра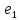 ,
, 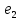 ,…,
,…,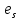 и
и все вершины графа G , являющимися концами этих ребер .
Граф , у которого каждая пара вершин соединена ребром , называется полным
графом . Полный граф с n вершинами обозначается
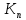 . Граф
. Граф 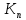 содержит
содержит 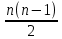
ребер .
Граф , который не имеет ни одного ребра называется пустым .
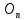
– пустой граф с
n вершинами .
Граф с n вершинами называется помеченным, если его вершины занумерованы от 1 до n.Два помеченных графа считаются равными , если множества вершин и ребер у них совпадают .
Теорема . Число помеченных графов сn вершинами равно
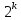 , где k=
, где k= .
.Доказательство . Рассмотрим множество V={1 , 2 ,…,n } всех вершин графа и множество
всех его потенциально возможных ребер E={ (1,1) ,…, (1,n) , …,(n-1 ,n) }.
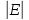 =K=
=K= .
.Для каждого ребра (i ,j)из множества E существует две возможности : ребро (i ,j) есть в графе или ребра (i ,j) нет в графе .Поэтому число различных помеченных графов равно
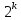 , где k=
, где k= .
.Определение . Граф Gназывается связным , если от любой его вершины можно по ребрам перейти к любой другой вершине .Будем говорить , что две вершины графа принадлежат одной компоненте . если от одной из них до другой можно перейти по ребрам графа .
Задача .Если для графа наименьшая степень его вершин
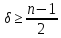 , то граф G связный .
, то граф G связный .Решение . Рассмотрим компоненту , содержащую наименьшее число вершин .В ней будет не более
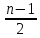 вершин . Но в таком случае степень любой вершины из этой компоненты будет не больше
вершин . Но в таком случае степень любой вершины из этой компоненты будет не больше 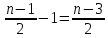 , что противоречит условию задачи .
, что противоречит условию задачи .Задача .Если граф с
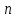 вершинами имеет больше , чем
вершинами имеет больше , чем 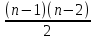 ребер ,то он связный .
ребер ,то он связный .Решение . Рассмотрим несвязный граф с
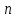 вершинами ,который имеет наибольшее число ребер . Этот граф имеет ровно две компоненты , каждая из которых является полным графом .Пусть большая из компонент имеет p вершин (значит p
вершинами ,который имеет наибольшее число ребер . Этот граф имеет ровно две компоненты , каждая из которых является полным графом .Пусть большая из компонент имеет p вершин (значит p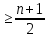 ) , тогда меньшая –
) , тогда меньшая –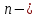 p
p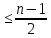
.число ребер в графе будет
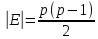 +
+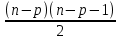 =
=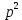 -np+
-np+ .
.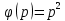 -np+
-np+ .
.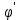 (p)=2p-n =2(p-
(p)=2p-n =2(p-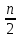 ) .Приp
) .Приp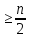 значение квадратного трехчлена растет . Наибольшее p при котором граф будет несвязным равно
значение квадратного трехчлена растет . Наибольшее p при котором граф будет несвязным равно  1.Одна компонента такого графа будет
1.Одна компонента такого графа будет 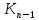 , а вторая – граф
, а вторая – граф 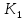 .Число ребер в графе
.Число ребер в графе 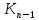 равно
равно  . а граф который получается из условия задачи имеет больше , чем
. а граф который получается из условия задачи имеет больше , чем 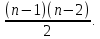 значит он связный .
значит он связный .Определение .Пусть задан граф G . Рассмотрим граф
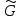 , который имеет такое же множество вершин . что и граф G , а ребро соединяет две вершины графа
, который имеет такое же множество вершин . что и граф G , а ребро соединяет две вершины графа 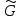 тогда и
тогда и только тогда , когда эти вершины не соединены ребром в графе G . Граф
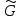 называется
называетсядополнительным графом к графу G .
Задача . Из двух графов G и дополнительного к нему графа
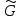 хотя бы один из них связен .
хотя бы один из них связен .Решение . Пусть граф G не является связным и состоит из компонент
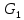 ,
, 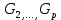 . Тогда в
. Тогда в дополнительном графе существуют ребра между любыми вершинами компонент
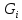 и
и 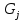
(i
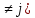
и граф
 будет связным .
будет связным .Определение .Граф , степени всех вершин которого одинаковы называется регулярным графом .
Определение . Граф , у которого существуют пары вершин , соединенные несколькими ребрами , называется мультиграфом .
Лемма о рукопожатиях .Сумма степеней вершин графа равна удвоенному числу ребер .
Следствие . Число вершин нечетной степени в графе четное .
Доказательство леммы .В сумме степеней вершин графа каждое ребро учитывается дважды .
Определение .Маршрутом в графе называется такая последовательность чередующихся вершин
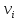 и ребер
и ребер 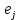 графа (
графа (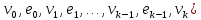 , что каждое ребро соединяет вершины последовательности , между которыми оно находится ,т.е. ребро
, что каждое ребро соединяет вершины последовательности , между которыми оно находится ,т.е. ребро 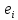 соединяет
соединяет вершины
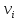 и
и 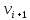 .Вершины
.Вершины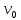 и
и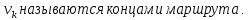 Если концы маршрута совпадают , то маршрут называется замкнутым .
Если концы маршрута совпадают , то маршрут называется замкнутым .Маршрут . в котором все ребра различные называется цепью . Про цепь говорят , чтоона соединяет свои концы .
Цепь в графе можно задавать перечислением только вершин или только ребер .Цепь , в которой первая и последняя вершины совпадают , называется циклом .
Цепь графа называется простой цепью ,если все ее вершины , кроме возможно крайних различны .Цикл графа называется простым циклом , если все его вершины кроме первой и последней различны . Простой цикл с p вершинами обозначается
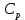 .
.Определение .Ориентированная простая цепь называется путем ,ориентированный простой цикл называется контуром .





 1 4 7 Ориентированный маршрут
1 4 7 Ориентированный маршрут







 2 5 8 1
2 5 8 1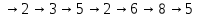

 3 6 9
3 6 9Замкнутый ориентированный маршрут 1
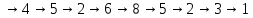 .
.Ориентированная цепь : 4
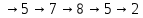 . Замкнутая ориентированная цепь :
. Замкнутая ориентированная цепь :6
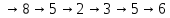 .Пример пути . соединяющего вершины 3 и 9 :
.Пример пути . соединяющего вершины 3 и 9 :3
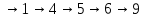 .Пример контура : 5
.Пример контура : 5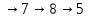 .
.Определение. Длиной маршрута называется число ребер в нем с учетом повторения .
Определение .Длиной цепи называется число содержащихся в ней ребер .
Определение . Расстоянием между двумя вершинами графа называетсянаименьшаяиз
длин цепей , соединяющих эти вершины . Сама такая цепь называется геодезической . Расстояние между вершинами uиv обозначается d(u , v).
Определение .Самая длинная геодезическая цепь называется диаметром графа . Длину диаметра будем называть диаметром и обозначать D.
Пример



 2 6 9
2 6 9