Файл: Вершинами графа, элементы множества e называются ребрами графа а пара (V, e ), т е. множество вершин и ребер графа называется графом. Если две вершины графа соединены ребром, то такие вершины называются смежными.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 79
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


 ) a• •b 2) a• •b 3) •b
) a• •b 2) a• •b 3) •b



 •c a• •c
•c a• •c


 c• •s d• •e •d
c• •s d• •e •d
 •d •e
•d •e-




 •b 5) a• •b
•b 5) a• •b



 •h
•h




 a• •g •I •cc• •d
a• •g •I •cc• •d

 •f •j e• •f
•f •j e• •f
 e• •d g• •h
e• •d g• •h6. Докажите , что если граф содержит цикл от вершины vк ней самой , то он содержит простой цикл от вершины vк ней самой .
7 . Докажите , что ориентированный граф является сильно связным , если в графе существует вершина v такая, что каждая другая вершина графа достижима из v и вершина v достижима из любой вершины графа.
8 . Ориентированный граф имеет эйлеров цикл тогда и только тогда , когда он сильно связный и степень входа каждой вершины равна ее степени выхода .
Матрицы инцидентности и смежности .
Определение .Пусть G –граф .B –матрица , строки которой обозначены вершинами графа, а столбцы обозначены ребрами графа . Будем считать , что вершины и ребра графа пронумерованы . B=(
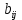 )
) 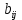 =
=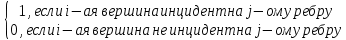
B
называется матрицей инцидентности .
 •a
•a



b
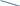 •
• 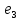 •c
•c 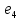 •d
•d 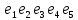
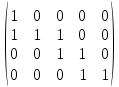
Определение .Пусть G –ориентированный граф .B –матрица , строки которой обозначенывершинами графа и столбцы обозначены теми же вершинами в том же самом порядке . B=(
 )
) =
=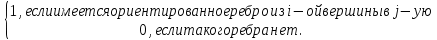
B называется матрицей смежности графа G .
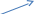
 •b
•b
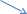
 a• •d
a• •d•c
a b c d

Важным применением матрицы смежности является возможность находить пути фиксированной длины k .
Определение . Для положительных целых чисел mи nматрицей m
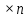 или
или массивом m
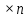 называется функция А={1,2,…,m}
называется функция А={1,2,…,m}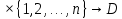 .
.Определение .Булевой матрицей называется матрица , каждый элемент которой есть 0 или 1 .
Определение булевых операций V и Ʌ на множестве {0,1}.
| V | 0 | 1 | | Ʌ | 0 | 1 |
| 0 | 0 | 1 | | 0 | 0 | 0 |
| 1 | 1 | 1 | | 1 | 0 | 1 |
Пусть Aи Bбулевы матрицы размера m
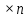 , а С -булева матрица размера n
, а С -булева матрица размера n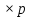 .
.Тогда 1) U=AVBопределяется соотношением
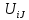 =
=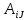 V
V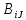 , 1
, 1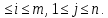
2)I=AɅBопределяется соотношением
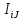 =
=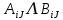
, 1

-
D=AʘCопределяется соотношением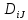 =
=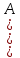 Ʌ
Ʌ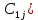 V
V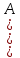 Ʌ
Ʌ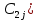 V…
V…
V
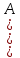 Ʌ
Ʌ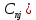 , 1
, 1
A=
 – матрица смежности ориентированного графа .
– матрица смежности ориентированного графа .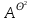 =
= ʘ
ʘ =
=
Теорема . Пусть G –(ориентированный ) граф с вершинами
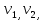 …,
…,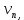 и матрицей смежности А . Путь длины kили k-путь из
и матрицей смежности А . Путь длины kили k-путь из  в
в  для 1
для 1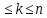 существует тогда и только тогда , когда
существует тогда и только тогда , когда 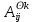 =1.
=1.Теорема . Пусть G –(ориентированный ) граф с вершинами
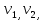 …,
…,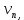 и матрицей смежности А . Из вершины
и матрицей смежности А . Из вершины  в вершину
в вершину  имеется mпутей длины k , где 1
имеется mпутей длины k , где 1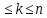
тогда и только тогда , когда
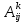 =m , где
=m , где 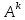 =A
=A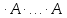 обычное умножение матриц .
обычное умножение матриц . =
=
Теорема . Пусть G –(ориентированный ) граф с вершинами
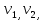 …,
…,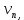 и матрицей смежности А . Пусть
и матрицей смежности А . Пусть 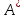 =AV
=AV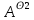 V
V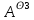 V… V
V… V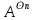 . Тогда
. Тогда 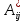 =1 тогда и только тогда , когда существует путь из
=1 тогда и только тогда , когда существует путь из  в
в  .
.Теорема . Пусть G –(ориентированный ) граф с вершинами
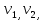 …,
…,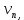 и матрицей смежности А. Пусть
и матрицей смежности А. Пусть 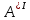 =
=