Файл: Вершинами графа, элементы множества e называются ребрами графа а пара (V, e ), т е. множество вершин и ребер графа называется графом. Если две вершины графа соединены ребром, то такие вершины называются смежными.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 81
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1 3 5
4 7 8d(1 ,5 )=2 , d(1 ,9 )=3 , d(4 ,9 )=3 .D=3.
Ярусом вершины vпорядка n(обозначается D(v , n)) , n=1 , 1 , 2 ,… называется множество вершин , находящихся от вершины v на расстоянии n .
Теорема .Пусть G=G (V , E ) –граф . Если существует путь из вершины
в вершину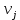
, тогда существует простой путь из вершины в вершину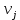 .Д
оказательство .
удаляем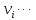
Теорема . Граф G является связным тогда и только тогда , когда между любыми двумя его вершинами существует простой путь .
Определение. Пусть G=G (V , E ) – граф . Подграф
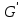графа G называется компонентой графа G, если выполнены следующие условия :- 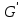- непустой связный подграф .
-
Если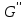
- связный подграф графа G и 
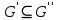, тогда 
.
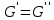Значит
- максимальный связный подграф графа G .Определение .Граф , вершины которого можно разбить на два множества ( две доли ) таким образом , что каждое ребро будет соединять вершины из разных множеств , называется двудольным . Двудольный граф обозначается G(
, 
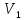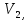E). Полный двудольный граф , у которого 
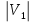=m ,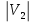 
=n, обозначим 
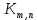.Если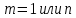 
=1 , то граф называется звездой . Определение. Если каждая вершина графа отмечена , то он называется размеченным .
Пример .Теорема ( Кенига ). Для того , чтобы граф был двудольным , необходимо и достаточно , чтобы он не содержал циклов нечетной длины .
Доказательство .⇒ Пусть G(
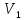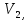, E)-двудольный граф , в котором существует цикл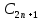
нечетной длины .Пусть
=
-…-
-
-
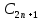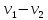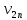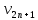. Не ограничивая общности можно считать , что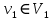 
. Тогда 
,…, 
, 
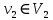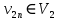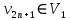, то есть ребро (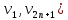
соединяет вершины из одной доли –противоречие .
Пусть все простые циклы графаG(V, E) имеют четную длину . Граф G можно считать связным . Разобьем вершины графа G на два непересекающихся множества
и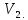
-
Включим во множество произвольную вершину v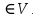
-
Выделим ярусы вершины v:D(v,0) , D(v ,1) , D(v , 2),….Вершины ярусов D (v , 2k+1 ),
K=1 , 2 ,… включим во множество
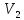.Вершины ярусов D (v , 2k )включим во множество . Тогда 
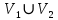=V;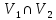 
=
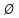.Предположим , что в графе GЕсть вершины ,принадлежащие одной доле и соединенные ребром .
Пусть для определенности u , w
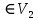.u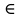
D(v , 2n+1), 
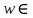D(v , 2m+1). Рассмотрим геодезические , соединяющие вершину v с вершинами u иw. Обозначим их 
, 
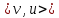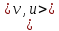и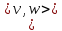 
.В силу сказанного 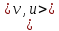=2n+1 , 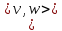=2m+1 .Эти геодезические имеют общие вершины , например,
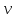. Пусть 
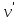- наиболее удаленная от вершины 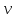общая вершина геодезических . Может оказаться , что 
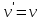. Так как 
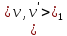и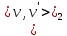 
- это участки геодезических , то 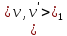и и 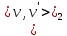- это геодезические соединяющие вершины 
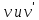. Значит они имеют одинаковую длину , 
=
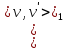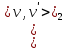=k . Тогда длина простой цепи 
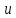−w-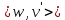
-
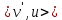равна 1+(2n+1-k)+(2m+1-k)=1+2m+2n-2k–нечетноечисло . Противоречие .
Теорема о сумме степеней вершин двудольного графа .
Суммы степеней вершин двудольного графа равны .
Доказательство . Пусть
, 
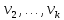– вершины одной доли , а 
, 
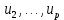– вершиныдругой доли . Тогда из одной доли выходит 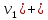d(
d(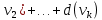
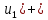ребер , а из другой d(
d(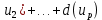
ребер . Равенство сумм следует из того , что это одни и те же ребра .Определение . Граф называется n – дольным , если все его вершины можно разбить на
n частей ( долей ) так , что каждое ребро будет иметь свои концы в разных долях .
Определение . Связный граф , в котором отсутствуют циклы называется деревом . Граф , в котором отсутствуют циклы называется лесом .
В любом дереве есть висячая вершина.
Доказательство .Предположим противное . Рассмотрим произвольную вершину
и Перейдем из нее по любому ребру (
, 
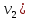в вершину 
. Поскольку степень вершины не меньше двух , то из нее по новому ребру можно в вершину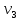 
и т.д. Но число вершин в графе Gконечно .Поэтому мы в конце концов придем в одну из вершин , в которой уже были . Это означает существование цикла , что противоречит условию .Каждое дерево имеет висячую вершину .Удалим висячую вершину
из дерева G вместе с ребром , выходящим из
будет связным ,и в нем нет циклов , то есть 
– дерево .Продолжим эту процедуру для
и построим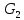 
. В итоге придем к дереву , состоящему из одной вершины . Получаем равенство m=n-1 , где
m – число ребер . а n – число вершин дерева . таким образом в любом дереве число ребер будет на единицу меньше числа вершин .
Задача . В связном графе , у которого число ребер на единицу меньше числа вершин нет циклов .
Р
ешение . Предположим противное : Граф G содержит цикл .поставим в соответствие каждой вершине цикла ребро цикла , которое выходит из этой вершины , если проходить цикл по часовой стрелке . Для каждой вершины , не принадлежащей циклу , выделим
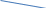
цепь , соединяющую . вершину с циклом и содержащую наименьшеечисло ребер .( Если таких цепей будет несколько , возьмем любую ) . Каждой такой вершине поставим в соответствие ребро выделенной цепи идущее от вершины к циклу . Таким образом каждой вершине графа будет поставлено в соответствие ребро , причем различным вершинам будут поставлены в соответствие различные ребра .Поэтому в графе ребер будет не меньше , чем вершин .
Теорема . Связный граф , имеющий n вершин и mребер , является деревом тогда и только тогда , когда m=n-1.
Теорема . Для графа G , имеющего n вершин и mребер следующие утверждения эквивалентны .
•G- дерево ;
• G – связный граф и m=n-1;
•G – граф без циклов и m=n-1;
•Любые две несовпадающие вершины графа G соединяет единственная простая цепь .
Импликации G- дерево
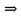G – связный граф и m=n-1⇒G – граф без циклов и m=n-1 уже доказаны .Докажем импликацию : G – граф без циклов и m=n-1⇒Любые две несовпадающие вершины графа G соединяет единственная простая цепь .Доказательство . Предположим , что для некоторых вершин aи b путь из aв b не является единственным .Пусть существуют два различных пути :