ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2.1. Выделение в блоке группы интегральных показателей (факторов), по изменению которых можно судить об общих тенденциях в данной сфере. Например, фактор “Дефицит бюджета” обобщенно характеризует ситуацию в бюджетной сфере.
2.2. Выделение в блоке показателей (факторов), характеризующих тенденции и процессы в данной сфере более детально. Например, факторы “Государственные закупки”, “Государственные трансфертные платежи” и др. более конкретно характеризуют ситуацию в бюджетной сфере.
3. Определение связей между факторами:
3.1. Определение связей и взаимосвязей между блоками факторов. Это позволит определить основные направления влияния факторов разных блоков друг на друга.
3.2. Определение непосредственных связей факторов внутри блока:
3.2.1. Определение направления влияний и взаимовлияний между факторами. Например, фактор “Уровень налогового бремени” влияет на “Неплатежи налогов”.
3.2.2. Определение позитивности влияния (положительное, отрицательное, +\-) Например, увеличение (уменьшение) фактора “Уровень налогового бремени” увеличивает (уменьшает) “Неплатежи налогов” – положительное влияние, а увеличение (уменьшение) фактора “Собираемость налогов” уменьшает (увеличивает) “Неплатежи налогов”.
3.2.3. Определение силы влияния и взаимовлияния факторов (слабо, сильно). Например, увеличение (уменьшение) фактора “Уровень налогового бремени” “значительно” увеличивает (уменьшает) “Неплатежи налогов”.
3.3. Определение связей между факторами различных блоков.
4. Проверка адекватности модели, т. е. сопоставление полученных результатов с характеристиками системы, которые при тех же исходных условиях были в прошлом. Если результаты сравнения – неудовлетворительны, то модель корректируется и переходят к п.
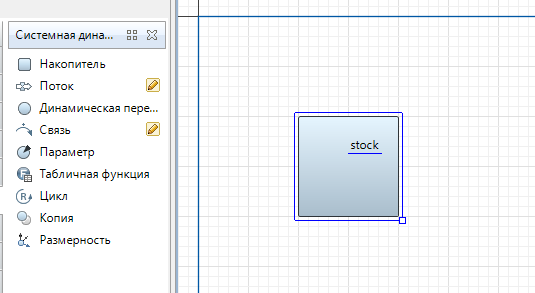
Системная диаграмма
Структурно модель системной динамики включает следующие элементы:
1) Уровни (накопители)
Уровни характеризуют накопленные значения величин внутри системы (заготовки, товары, банковская наличность, уровень оптимизма и т.д.)
Уровни представляют собой значения переменных, накопленные в результате разностей между входящими и выходящими потоками. Каждый уровень описывается переменной величиной
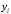
, зависящей от разностей.
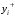
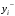
Уравнение уровня:
Новый уровень= Текущий уровень+ Входящий поток-Выходящий поток.
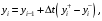
в дифференциальной форме:
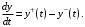
2) Потоковая связь ( ) – дуга потоковой диаграммы, связывает уровни с уровнями, истоками и стоками. Проходит через темп.
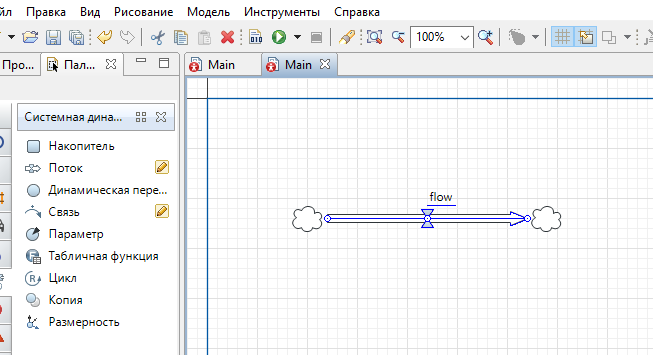
3) Темп ( ) – обозначает скорость потока, проходящего по соответствующей дуге потоковой сети. 
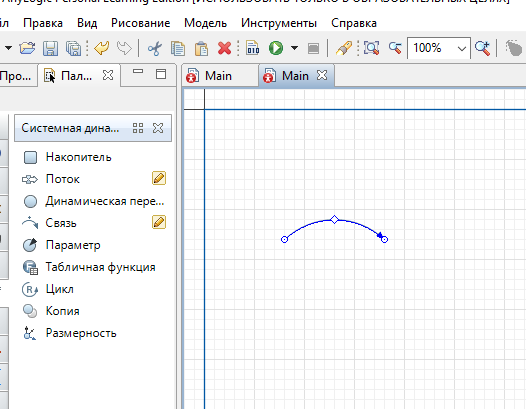
4) Озеро ( ) – нулевой уровень потоковой сети.5)Информационная связь – может соединять параметры, переменные и уровни с темпами, переменными и выходами
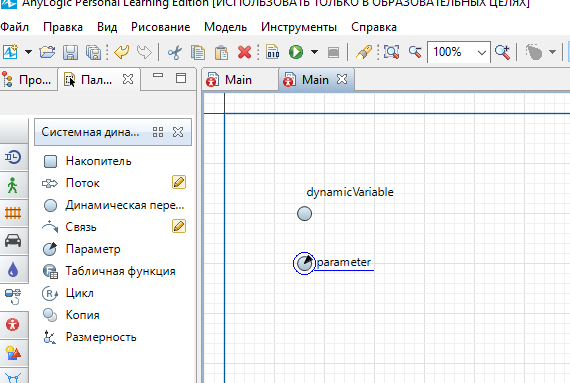
6) Переменная и параметр
Модель развития эпидемии
В современном здравоохранении одной из актуальных проблем является профилактика и предотвращение массового распространения инфекционных заболеваний различной природы. Скорость распространения эпидемии зависит от принимаемых в здравоохранении мер (в том числе вакцинации), влияющих на параметры процессов инфицирования и выздоровления. Поэтому исследование процесса развития эпидемии в целях предотвращения массовых заражений, является в настоящий момент социально значимой задачей.
В своих исследованиях мы опирались на классическую математическую модель развития эпидемии, описанную в работе [3]. В данной модели исследуется зависимость динамики числа заболевших (например, гриппом) и выздоровевших после болезни.
Постановка задачи. Рассмотрим сложную систему – общество, элементами которого являются люди. Выделим следующие группы (подсистемы) людей:
● инфицированные (заболевшие гриппом к определенному моменту времени);
● выздоровевшие (выздоровевшие после болезни гриппом);
● не вакцинированные (восприимчивые к гриппу);
● вакцинированные (невосприимчивые к гриппу).
Параметрами процесса развития эпидемии выступают:
● infection_rate (темп заболевания) – доля заболевающих гриппом в единицу времени (от 0 до 1) среди восприимчивых к гриппу людей;
● recovery_rate (темп выздоровления) – доля выздоравливающих в единицу времени (от 0 до 1) среди всех людей, заболевших гриппом.
Требуется: провести исследование динамики численности группы инфицированных и группы выздоровевших людей в зависимости от параметров процесса развития эпидемии и начальной численности всех групп населения.
Построение модели. Имитационная модель развития эпидемии относится к классу моделей системной динамики. Для наглядного представления такого типа моделей принято строить потоковые диаграммы. Элементами потоковой диаграммы для данного примера являются:
1) Уровни (узлы сети, обозначающие переменные состояния модели):
● susceptible (не вакцинированные) – общее число людей, восприимчивых к гриппу;
● infected (инфицированные) – общее число людей, заболевших гриппом;
● recovered – общее число людей, выздоровевших после болезни.
2) Постоянныепараметры: infection_rate; recovery_rate;
3) Темпы (скорость потока, проходящего по дуге потоковой сети):
●
●
●
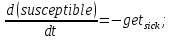
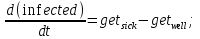
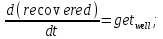
где темпы
● get_sick – число людей, заболевших в единицу времени,
get_sick = infected*susceptible*infection_rate;
● get_well – число людей, выздоровевших в единицу времени,
get_well = infected*recocery_rate.
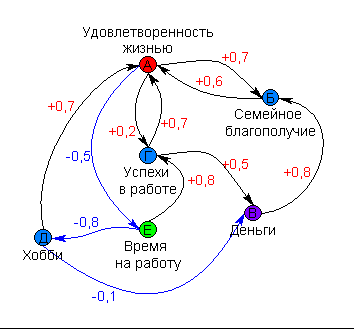
Потоковая диаграмма модели изображена на рис.11.
Susceptible
Recovered
Infected
get_sick
get_well
Recovery_rate
Infection_rate
Потоковая диаграмма развития эпидемии
Реализация модели в системе AnyLogic-ple-7.3.6:
