ФГБОУ ВО «ЧГУ имени И.Н. Ульянова»
Кафедра «Общей физики»

Лабораторная работа №1

Измерение линейных размеров и объемов твердых тел правильной формы

Работу выполнили:

студенты группы:

РЭА-42-22

1.Ярусов Даниил Евгеньевич

2.Горшков Антон Александрович

Допуск

Выполнение

Защита

Чебоксары 2023

1. Цель работы - ознакомление с основными положениями теории погрешностей, статистической обработкой результатов измерений, а также правилами и приемами измерений линейных и угловых величин.

2. Приборы и принадлежности: штангенциркуль, микрометр, кольцо.

3. Теория.

Для определения линейных размеров тел применяются самые различные измерительные приборы, выбор которых определяется необходимой точностью и условиями эксперимента. Наиболее простым из них является масштабная линейка с миллиметровыми делениями. Цена деления масштабной линейки 1 мм. При измерениях такой линейкой максимальная погрешность не превосходит половины цены деления, т.е. 0,5 мм.

Штангенциркуль служит для линейных измерений, не требующих высокой точности, и состоит из линейки с миллиметровым делением, вдоль которой может перемещаться подвижная рамка. На подвижной рамке нанесен линейный нониус с числом делений m (10 или 20). Погрешность штангенциркуля равна точности нониуса (иногда половина точности нониуса).


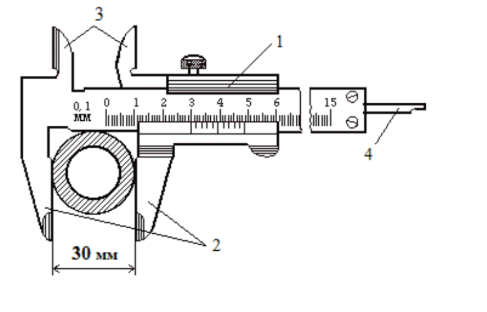
Нониус – дополнительная шкала к обычному масштабу, позволяющая повысить точность измерений в 10-20 раз. Линейный нониус представляет собой небольшую шкалу, скользящую вдоль основной шкалы.



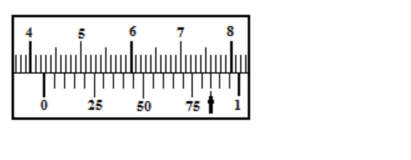
На этом штангенциркуле получается значение 42, 8 мм


Микрометр имеет вид тисков, в которых измеряемый предмет зажимается с помощью винта. На стержне винта укреплен барабан с нанесенной на нем шкалой. Отсчетное устройство состоит из грубой точной шкал.

---

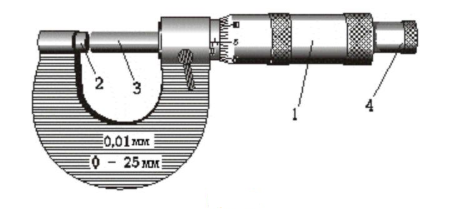
Перед началом измерений необходимо проверить нулевой отсчет микрометра. При измерении предмет зажимается между упором и стержнем винта с помощью трещотки. По грубой шкале отсчитывается размер предмета с точностью до мм. По шкале барабана отсчитываются сотые доли миллиметра. Результат получается суммированием показаний двух шкал.



На этом микрометре получается значение 2, 60 мм.

ИЗМЕРЕНИЯ

Объем тела, имеющего форму плоского цилиндрического

кольца, можно вычислить по формуле:


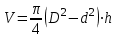
где D, d - внешний и внутренний диаметры; h - толщина кольца. Для измерения D и d следует воспользоваться штангенциркулем.


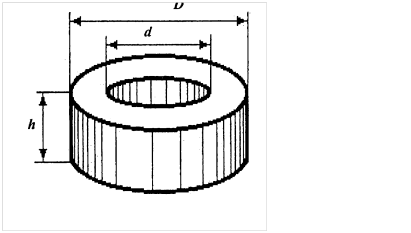
Измерения диаметров кольца делаются штангенциркулем, а измерения толщины кольца следует проводить микрометром. Перед началом измерений необходимо изучить краткую теорию нониуса, а также правила пользования измерительными инструментами (штангенциркуль, микрометр). Все измерения проделываются по несколько раз (не меньше пяти) в различных местах кольца.
4. Результаты и расчеты.
Таблица.

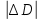1	D, мм	, мм	d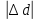, мм	, мм	h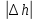, мм	, мм
1	56,1	0,23	44,9	0, 02	18,44	0,01
2	56,0	0,15	45,0	0,13	18,41	0,02
3	55,7	0,16	44,8	0,09	18,45	0,02
4	55,8	0,07	44,9	0,09	18,49	0,04
5	55,7	0,16	44,8	0,03	18,39	0,04
Ср.	55,86		44,88		18,43

---

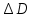_пр. =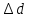 _пр.=0,1 мм

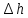_пр. =0,01 мм

Вычисления случайной погрешности и полной погрешности прямых измерений:
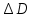_сл. =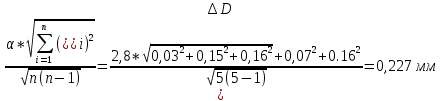

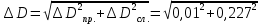=0,225 мм

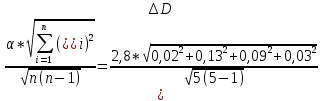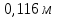_сл.= = м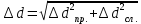
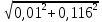= =0,116мм


h_сл. =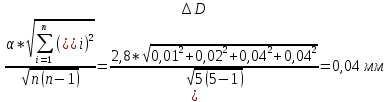


= =


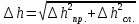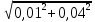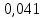
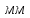
Вычисление среднего значения объема кольца в


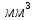
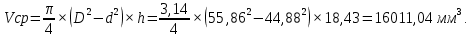
Вычисление относительной погрешности объема кольца:

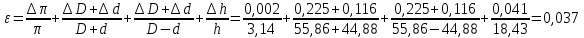
Вычисление абсолютной погрешности объема кольца
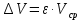
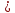0,037× 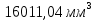= 592,41 мм³

5. Ответ: Истинное значение объема кольца с учетом абсолютной ошибки косвенного измерения равняется

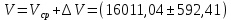мм³ =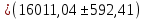

10 ^{– 9} м³

Контрольные вопросы и ответы (писать вопрос и краткий ответ, см. 2-й вопрос и его ответ)

---

1. 
   Что такое доверительный интервал и доверительная вероятность?
   

Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.
Вероятность, с которой в условиях данного эксперимента полученные экспериментальные данные можно считать надежными (достоверными), называют доверительной вероятностью

2. 
   Как находится абсолютная погрешность прямых измерений?
   

Абсолютная погрешность прямых измерений определяется по формуле:
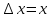_{среднее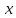} – _{измеренное}

3. 
   Как вычислить абсолютные и относительные погрешности
   

косвенных измерений?
Если один из множителей представляет собой сумму или разность, нужно предварительно найти его абсолютную погрешность (сложением абсолютных погрешностей слагаемых), а затем относительную. Зная относительную погрешность, найти абсолютную погрешность измерений можно так: ΔА = ε_A· А.

4. 
   Как оцениваются приборные погрешности?
   

Если класс точности используемого прибора известен, то величина приборной погрешности оценивается по формуле

,

где - класс точности прибора, x_max – выбранный верхний предел измерения прибора. Обычно класс точности может иметь одно из следующих значений: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0.

5. 
   Чему равна погрешность табличных значений?
   

Погрешность табличных значений равна 0.1мм

6. 
   Как устроен линейный нониус, где он применяется и чему равна его точность?
   

Разность b–f=b/m называется точностью нониуса, то есть точность нониуса b/m равна отношению цены наименьшего деления масштаба к числу делений на нониусе. Точность нониуса часто бывает равна 1/10 мм; в этом случае b=1 мм, m=10.

Нониус применяется для измерения глубин отверстия

---

Смотрите также файлы

• Отчет о проведении Недели психологии в школе по теме.docx

• Протокол от .doc

• Задания по географии для подготовки к итоговой аттестации Часть А.docx

• География пнінен орытынды аттестаттауа дайынды тапсырмалары а блімі.docx

• Электроизмерительные приборы4 1 Основные понятия и общие сведения из теории измерений4.docx