Министерство образования и науки Российской ФедерацииФедеральное государственное бюджетное образовательноеучреждение высшего образования«Кузбасский государственный технический университет имени Т. Ф. Горбачева»

2. Кафедра физики

Отчетпо лабораторной работе № 3 Определение момента инерции при помощи крутильного маятникаВыполнил ст. группы Амосов С.А.(Ф.И.О.)ПреподавательФофанов А.А.(Ф.И.О.)

	Дата	Роспись
Допуск
Отчет

Кемерово 2023

1. 
   Цель работы: освоение метода экспериментального определения момента инерции тела при помощи крутильных колебаний.
   

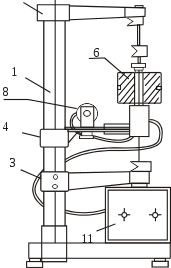
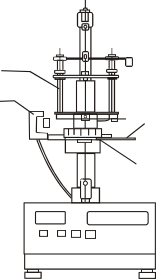
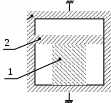
2. Приборы и принадлежности:стандартный крутильный маятник FРМ-05, линейка, эталонное тело.3. Описание и схема лабораторной установки: 259710Рис. 1. Крутильный маятник:1 – колонка; 2, 3, 4 – кронштейны; 5 – рамка; 6 – груз;7 – стальная плита; 8 – электромагнит; 9 – фотоэлектрический датчик; 10 – угловая шкала; 11 – миллисекундомер со счетчиком и кнопками управления.Рис. 2. Рамка крутильного маятника:1 – тело, момент инерции которого определяется; 2 – подвижная балка.

---

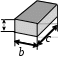
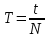
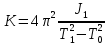
аРис. 3. Геометрическая форма исследуемых телa – высота эталонного тела, b – ширина эталонного тела, с- длина эталонного тела.4. Основные расчетные формулы: 1. Период крутильных колебаний:где T – Период крутильных колебаний; t – время колебаний; N – число колебаний (N = 10).2. Модуль кручения:гдеК – модуль кручения – коэффициент, определяемый упруги-ми свойствами проволоки; 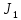– Момент инерции эталонного тела J₁ = 4,08⋅10⁻⁴ кг ⋅м²; 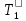– период колебаний рамки с эталонным телом; 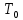– периоды колебаний ненагруженной рамки.3. Момент инерции ненагруженной рамки равен: 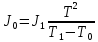,где ; 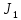– Момент инерции эталонного тела J₁ = 4,08⋅10⁻⁴ кг ⋅м²; 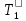– период колебаний рамки с эталонным телом; 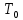– периоды колебаний ненагруженной рамки; T - период колебаний рамки; 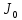- момент инерции ненагруженной рамки.4. Период колебаний рамки: 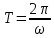,где T – период колебаний рамки;

---

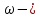
циклическая частота колебаний.
5. Циклическая частота колебаний:

,

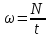где циклическая частота колебаний; N – число колебаний (N = 10); .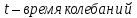
6. Теоретическое значение момента инерции параллелепипеда со сторонами а, b, с относительно оси а, b, c проходящей через центр масс:

,




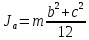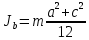
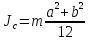
где 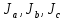– Теоретическое значение момента инерции параллелепипеда со сторонами а, b, с относительно оси а, b, c проходящей через центр масс; m – масса тела; а, b, c – стороны параллелепипеда.
7. Момент инерции закрепленного в рамке тела:

,

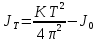где 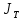- момент инерции закрепленного в ней тела; К – модуль кручения – коэффициент, определяемый упругими свойствами проволоки; T – период колебаний рамки; - момент инерции ненагруженной рамки.
8. Расхождение теоретических и экспериментальных значений:

,

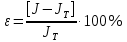где 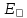– расхождение теоретических и экспериментальных значений; 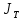– теоретические значения инерции; 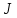–экспериментальное значение.


5. Таблицы

Таблица 1

№ п/п	t0i	N	T0i	T0	t1i	T1i	T1	К	J0
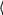	с		с	с	с	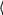с	с	кг·м2/с2	кг·м2
1		10
2
3
4
5

---

Расчет коэффициента К и момента инерции ненагруженной рамки J0где t0i –время колебаний ненагруженной рамки; N – число колебаний (N = 10); T0i – период крутильных колебаний ненагруженной рамки; ˂T0˃ - среднее значение периода крутильных колебаний ненагруженной рамки; t1i - время колебаний рамки с эталонным телом; T1i - период крутильных колебаний рамки с эталонным телом; ˂T1˃ - среднее значение периода крутильных колебаний рамки с эталонным телом; - момент инерции ненагруженной рамки; К – модуль кручения – коэффициент, определяемый упругими свойствами проволоки.Таблица 2Расчет моментов инерции параллелепипеда относительно осей, параллельных ребрам a, b, c

№ п/п

Ja = кг⋅м2

Jb = кг⋅м2

Jc = кг⋅м2

tai

N

Tai

Та

tbi

N

Tbi

Tb

tci

N

Tci

Тс

с

с

с

с

с

с

с

с

с

1

10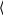

10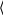

10

2

3

4

5

---

где 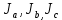- теоретическое значение момента инерции параллелепипеда со сторонами а, b, с относительно оси а, b, с проходящей через центр масс; ^tai, ^tbi,^tci – время колебаний относительно оси а, b, с;N – число колебаний (N = 10); ^Tai, ^Tbi, ^Tci – период колебания относительно оси а, b, с; 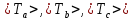- среднее значение периода колебаний относительно оси а, b, с.6. Примеры расчетов.7. Вывод

---

Смотрите также файлы

• С. В. Шекшеня М. Экономика 2015 С. 126.docx

• Синтез счётчика с асинхронной установкой.docx

• 2 Современные технологии производства пищевой продукции.docx

• Курсовая работа по дисциплине Разработка и эксплуатация защищенных автоматизированных систем (наименование дисциплины).docx

• Electronic Noses and Tongues Applications for the Food and Pharmaceutical Industries Elizabeth A. Baldwin, Jinhe Bai, Anne Plotto, and Sharon Dea.pptx