Файл: Коммуникаций российской федерации федеральное государственное бюджетное образовательное учреждение высшего образования.docx
Добавлен: 30.11.2023
Просмотров: 92
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
Кафедра информационных управляющих систем
ОТЧЁТ
по лабораторной работе №1
по дисциплине «Нейросетевые технологии»
Вариант 5
Выполнил: студент группы ИСТ-033
«18» апреля 2023 г. ________/Э.С. Виноградова
Принял: к.т.н., доцент Раковский О.В.
«18» апреля 2023 г.________/О.В. Раковский
Санкт-Петербург
2023
СОДЕРЖАНИЕ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» 1
(СПбГУТ) 1
ВВЕДЕНИЕ 3
Задание 1 3
Задание 2 3
ХОД РАБОТЫ 4
Задание 1 4
Задание 2 5
ЗАКЛЮЧЕНИЕ 8
ВВЕДЕНИЕ 3
ХОД РАБОТЫ 4
Задание 1 4
Задание 2 5
ЗАКЛЮЧЕНИЕ 8
ВВЕДЕНИЕ
Задание 1
Смоделировать заданную функцию на отрезке [0, 8] с использованием библиотеки neuralnet. Отчет должен содержать подготовку данных для обучения сети. Обоснование выбранной архитектуры. Структурную схему обученной сети с указанием весов. Графики моделируемой и смоделированной функций. Варианты заданий приведены в таблице 1.
Таблица 1
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» 1
(СПбГУТ) 1
ВВЕДЕНИЕ 3
Задание 1 3
Задание 2 3
ХОД РАБОТЫ 4
Задание 1 4
Задание 2 5
ЗАКЛЮЧЕНИЕ 8
| Вариант | Моделируемая функция |
| 0 | y = cos x / (sin 2x + 2) |
| 1 | y = sin x(arctg 0.5x) + cos x |
| 2 | y = 0.5 sin x + cos 2x + 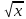 |
| 3 | y = cos x + x – sin 2x |
| 4 | y = 4 arctg x + sin x |
| 5 | y = A |
| 6 | y = sin x + x – cos 2x |
| 7 | y = 0.4 cos x + sin 3x + 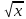 |
| 8 | y = 0.5 cos x + 1.5 arctg 0.2x + 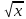 |
| 9 | y = sin 0.3x2 + 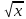 |
Задание 2
Подобрать структуру hidden и порог функции ошибки threshold для точной аппроксимации заданных последовательностей имульсов. Отчет по работе должен содержать структурную схему обученной сети без указания весов. Графики аппроксимируемой и полученной последовательности для нескольких приближений параметров hidden и threshold. Варианты заданий приведены в таблице 2.
Таблица 2
| Вариант | Последовательность импульсов |
| Четная цифра | x = seq(from = -9.5, to = 10, by = 0.5) y = rep(c(1,1,1,1,1,0,0,0,0,0), 4) |
| Нечетная цифра | x = seq(from = 0, to = 3.15, by = 0.05) y = rep(c(1,1,1,1,0,0,0,0), 8) |
ХОД РАБОТЫ
Задание 1
Смоделирована функция, с использованием библиеки neuralnet.
Сначала формируется фрейм данных learn для обучения сети (строка 5). Затем загружается библиотека neuralnet и формируется сеть netcos. В функции neuralnet() мы определяем минимальное число параметров: задаем формулу y x, определяем число нейронов в скрытом слое hidden = 4 и указываем имя фрейма learn с набором данных для обучения. Остальные параметры заданы по умолчанию (строка 7). Запуск функции на исполнение осуществляет обучение сети netcos.
Для проверки работы обученной сети создаем фрейм test (строка 11) с тестовыми данными. Функция predict() вычисляет реакцию обученной сети netcos в переменной yp. Листинг приведен на рисунке 1.
Приведен график моделируемой функции y, представленной 50 розовыми точками, и функции yp, сформированной сетью и представленной на графике 5000 черных точек. Графики аналогичны (рисунок 2). Структурная схема представлена на рисунке 3.
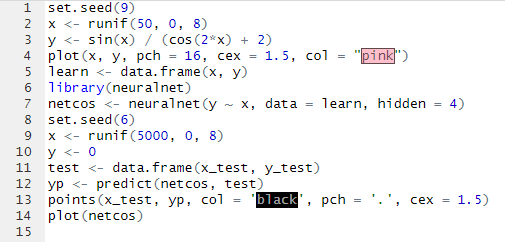
Рисунок 1
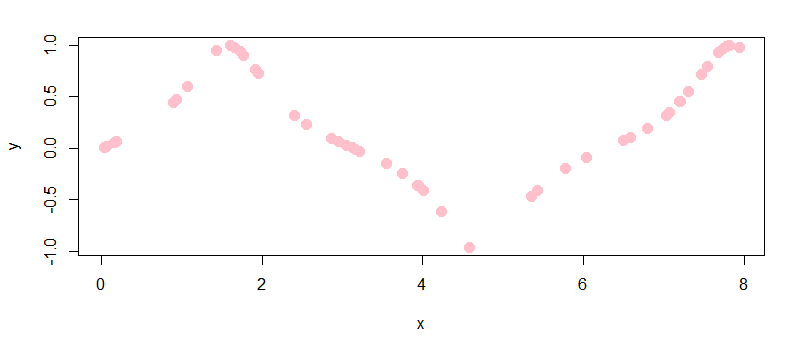
Рисунок 2
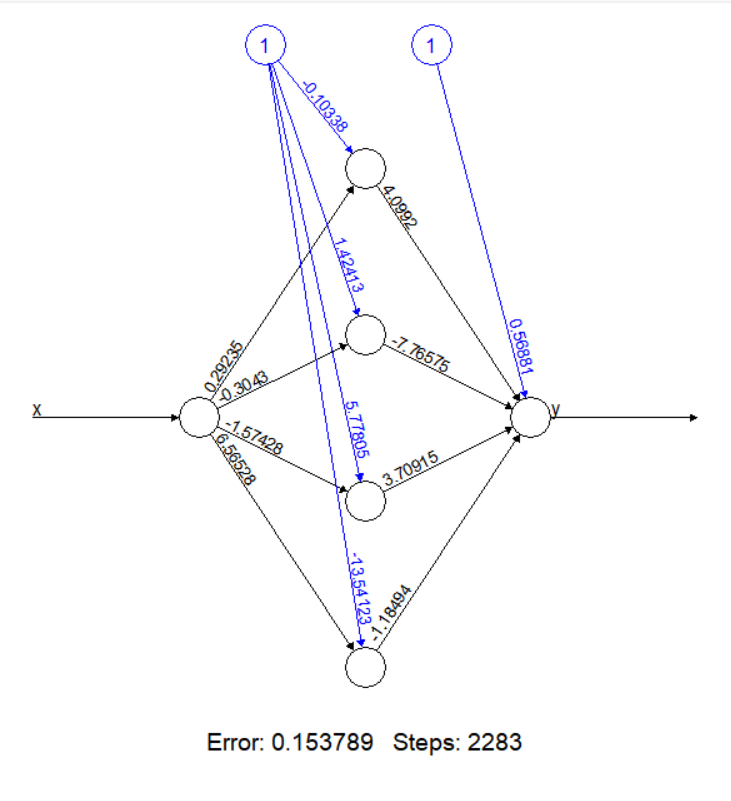
Рисунок 3
Задание 2
Создана последовательность импульсов x = seq(from = 0, to = 3.15, by = 0.05), y = rep(c(1,1,1,1,0,0,0,0), 8), а на неё наложен результат аппроксимации. Для построения жёлтой кривой была использована функция plot(x, y, type = ‘l’, col = “yellow”, lwd = 9), а для наложения чёрных - lines(x,yp). Результат представлен на рисунке 5. Листинг представлен на рисунке 4.
Для создания структурной схема обученной сети без указания весов задаём функцию plot(netcos, show.weight=FALSE). Если указать значение TRUE, то будут показаны весы, поэтому указано значение FALSE, чтобы их не было (рисунок 6).
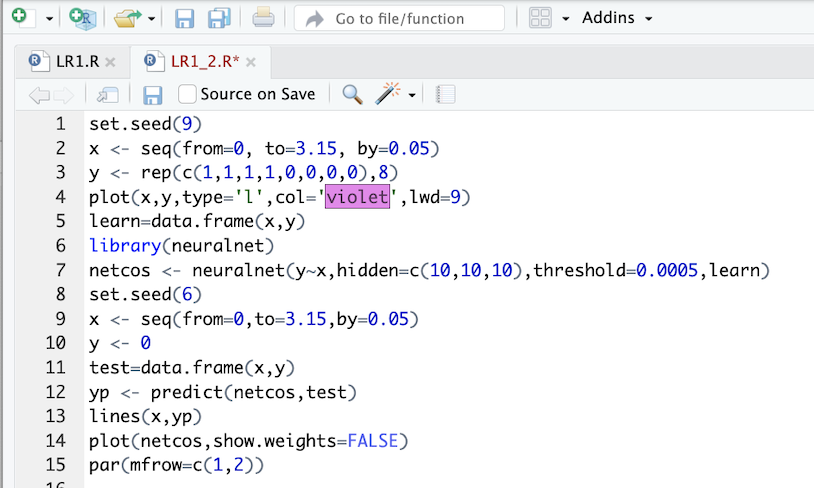
Рисунок 4
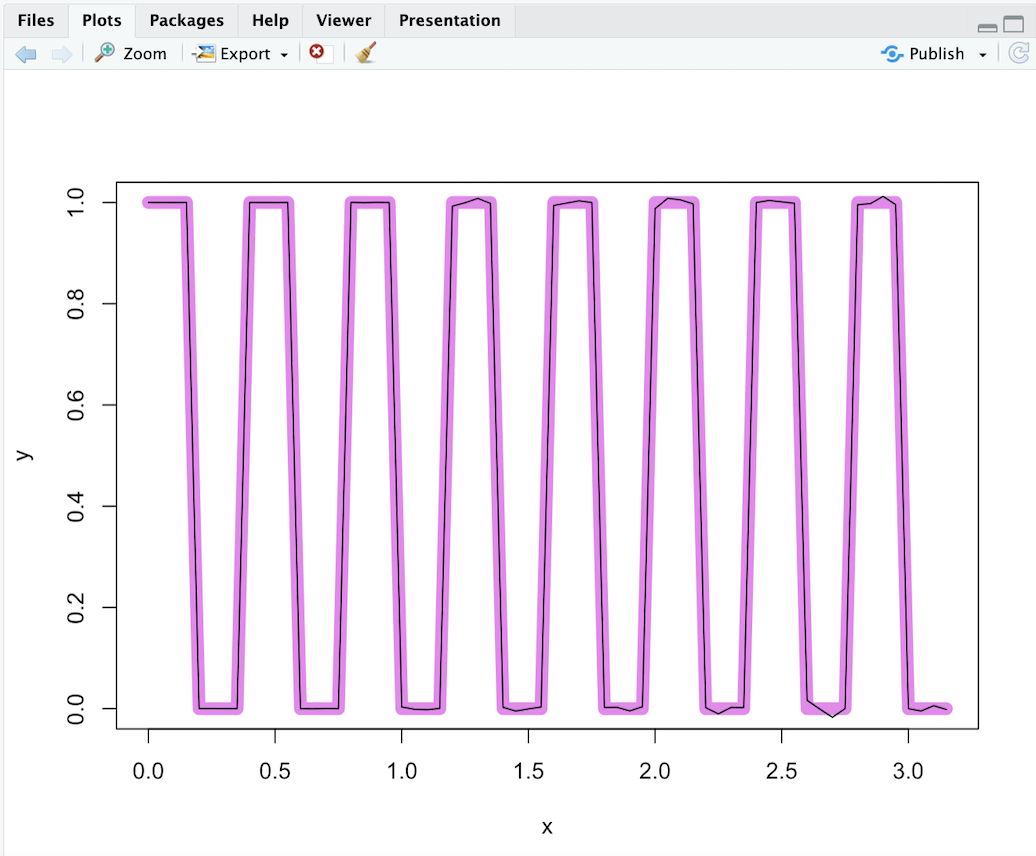
Рисунок 5
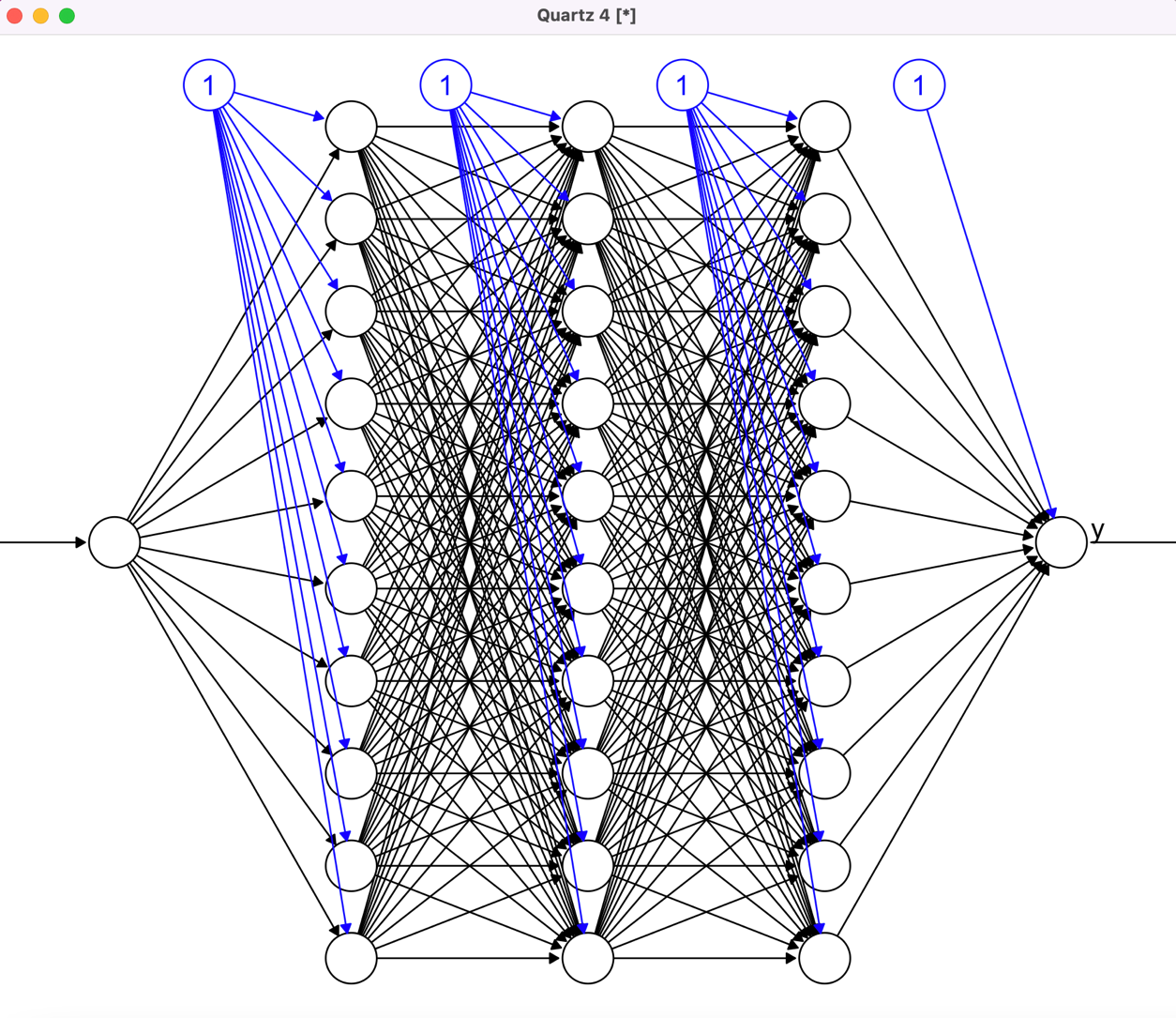
Рисунок 6
При увеличении количества слоев, значений нейронов и уменьшения значения threshold, графики сошлись более точно (рисунок 7). Графики представлены на рисунке 8. Структурная схема представлена на рисунке 9.
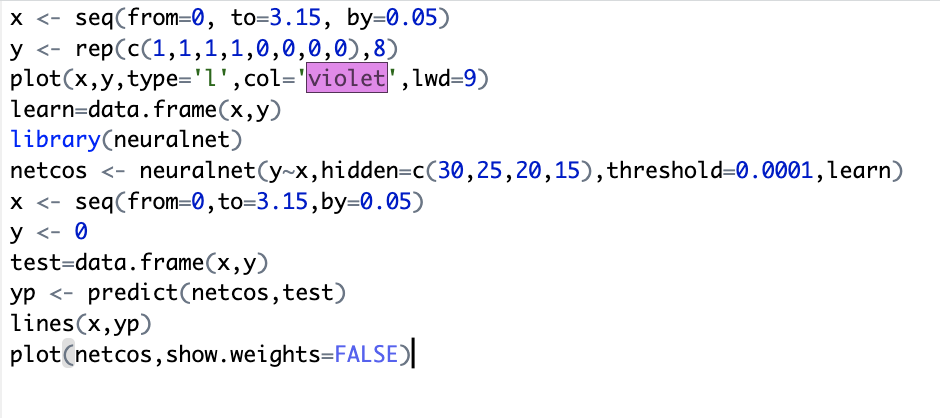
Рисунок 7
ЗАКЛЮЧЕНИЕ
В ходе лабораторной работы ознакомились со средой Rstudio, научились выполнять простейшие задачи по обучению сетей, смоделировали функцию на заданном отрезке. Подобрали структуру hidden и порог функции ошибки threshold для точной аппроксимации заданных последовательностей импульсов.