абс.-абсолютД-ДәлелдеуТ.-ТеоремаДәрежелік қатардың жинақтылық радиусын табу жолдары.A-Анықтама.R саны мынандай дәрежелік қатардың,бұндағы дәрежелік қатар 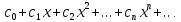жинақты болып табылады ,|x|R шартын барша x үшін теңсіздікті қанағаттандырса дәрежелік қатардың радиусы деп атаймыз.

Теорема.Дәрежелік 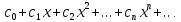қатардың жинақталу облысы ортасы сандар осінің санау басында жатқан (-R;R) аралығы болады дей аламыз,сонда аралықты 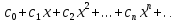. қатар абсолют жинақты болады.

Д.Жиын M= x дәрежелік қатардың кез келген кезде бар болатын жинақталу облысы болсын.K деп M жиынының барша сандардың абс. мәндерінен құралған жиынды белгілейік және R=supK болды делік.

R болуы мүмкін мына 3 жағдайды айқындалық:

Бір) R=0 болғанда,дәрежелік қатардың жалғыз түйір ғана жинақталыс x=0 болады.

Екі)R ақырлы шама,R n тең емес 0 ге және R тең емес шексіздікке болса,x 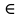M-тің 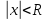теңсіздігін қанағаттандыратын әртүрлі мәні үшін нүкте 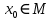табылып,мына теңсіздікті нақтылайды .

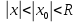Абельдің теоремасы арқылы 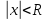теңсіздігі айқындалатын 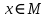үшін дәрежелік қатар жинақты.

Үш)R=+ 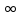болса,қандай көп мәнін 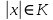мәнін алсақта, 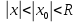теңсіздігін қанағаттандыратын x 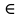M болады.

Бұл да Абель теоремасы абойынша 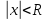теңсіздіг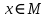ін үшін 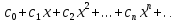. қатар абсолют жинақты.

А.Үстінде нақыталанған теоремадағы R шамасы 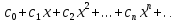. қатардың жинақтылыс радиусы,оның жинақтылыс интервалы (-R;R) дейді мыс.

Байқайтын бір мәселе: 」 Радиус тең емес нольге және тең емес шексіздікке болған жағдай кезінде (-R;R) аралығында 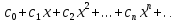. қатар жинақты немесе жинақсыз болуы мүмкін. 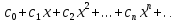. қатар үшін

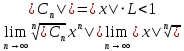теңсіздігі орындалатын болғанда , 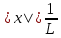кезінде абсолют жинақталады.

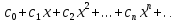. жинақтылыс радиусы үшін 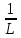шамасын,сонда R = 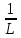қабылдауға болады.

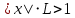」 ,болғанда қатар жинақталмайды.

Осы тұжырымдама сияқты,」 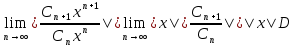<1 болса,R = 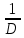болады.

Осылай дәрежелік қатардың жинақтылыс радиусын табу керек болса Коши немесе Даламбер белгісін қолданамыз.

Осы белгілер арқылы мысал қарастырып өтейік.Мысал, 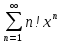жинақталыс радиусын табу керек.

Шешімі:D =

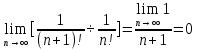
Сонда,радиус =+ 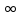,қатар барша нақты сандар жиынында жинақталады.

Екінші мысал)1+2x+(2x)^2+...+ (2x)^n +... жинақтылыс радиусын табу.

Шешімі: 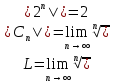,бұл жерде R = 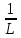=½

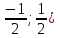( қатардың жинақтылыс интервалы болады.

Бізде x =-½ болғанда 1-1+1-1+...+| 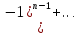сандық қатар шығады,бұда қатар жинақталмайды,себебі,дербес қосындысы ешқандай шекке ұмтылмайтындықтан.

x =½ болғанда,

1+1+1+...+1+... сандық қатар шығады да,ол да жинақталмайды.

Қатардың жинақтылыс облысы 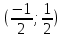болады. 1>

---

Смотрите также файлы

• казахский медицинский университет непрерывного образования департамент резидентуры лист овладения практическими навыками врачемрезидентом.docx

• Правовое регулирование воспитательной работы в образовательной организации Содержание.doc

• Служебная и профессиональная халатность проблемы разграничения.docx

• Задания 20. Короткий алгоритм в среде формального исполнителя или на языке программирования Вариант 20. 1.docx

• Реферат по дисциплине Архитектура эвм по теме Построение вычислительных кластеров.docx