Файл: 2 тема теория Информатика.doc

Тема №2. Архитектура современной вычислительной техники

Цель: Дать основное представление о структуре и функциях аппаратной части персонального компьютера. Научить различать основные типы персональных компьютеров.

Задачи обучения: Ознакомление с архитектурой современной вычислительной техники.

Ознакомление c внутренними и внешними устройствами компьютеров, основными средствами хранения документов.

Основные вопросы темы:

1. Представление информации в компьютере.

2. Булева алгебра и логические схемы компьютера.

3. Элементы организации основных блоков компьютера.

4. Архитектурная организация процессора.

5. Организация памяти компьютера.

6. Основные устройства, применяемые для долговременного хранения данных на ПК.

7. Логическая организация хранения данных на магнитных дисках.

8. Физическая организация хранения данных на магнитных дисках.

9. Состав ПК.

Методы обучения и преподавания: семинар

Теоретический блок

Медицина всегда была на переднем крае прогресса. Многие технические достижения внедрялись впервые в медицине. Так было и с перспективными разработками в области электроники, в частности компьютеров.

История применения компьютеров в медицине ведет отсчет с 1967 года, когда Олдендорф использовал примитивный ламповый ПЭВМ в первом магнитно-резонансном сканирующем томографе. Серийно же компьютеры стали применяться с 1971 года в МР-томографах Хаусфилда – инженера музыкальной компании EMI.

В настоящее время мир переживает настоящий компьютерный бум. Персональные компьютеры (ПК или РС) прочно входят в нашу жизнь и становятся вещью первой необходимости. Жизнь миллионов людей не мыслима без «персоналки» и медицина на данном этапе развития уже не может обойтись без «электронного помощника».

Возможности, которые предоставляет ПК, рано или поздно станут такими же обыденными, как и стетоскоп, и их придется осваивать.

Основным объектом внимания дисциплины «Информатика» является процесс информатизации и компьютеризации современного общества, который охватывает все сферы нашей жизни и развивается невиданными в истории темпами.

То, что связано с приобретением новых знаний об окружающем мире, ранее не известных человечеству, - называют наукой, а то, что связано с реализацией этих знаний в процессе создания и использования материальных и духовных ценностей, - называют технологией. Между этими понятиями нет четкой границы, и их нельзя противопоставлять друг дру­гу. Если наука стимулирует развитие технологии, то и технология стимулирует развитие науки.

Термином "Информатика" обозначают совокупность дисциплин, изучающих свойства информации, а также способы представления, накопления, обработки и передачи информации с помощью технических средств.

---

Теоретическую основу информатики образует группа фундаментальных наук, которую в равной степени можно отнести и к математике, и к кибернетике: теория информации, теория алгоритмов, математическая логика, комбинаторный анализ, формальная грамматика и т.д. Информатика имеет и собственные разделы: операционные системы, архитектура ЭВМ, теоретическое программирование и другие.

"Материальная" база информатики связана со многими разделами физики, с химией, и особенно - с электроникой и радиотехникой.

Ядро информатики - информационная технология как совокупность конкретных технических и программных средств, с помощью которых мы выполняем разнообразные операции по обработке информации во всех сферах нашей жизни и деятельности. Иногда информационную технологию называют компьютерной технологией или даже прикладной информатикой.

Центральное место в прикладной информатике занимает компьютер (от английского слова compute - вычислять) - техническое устройство для обработки информации.

Электронные вычислительные машины

Электронные вычислительные машины (ЭВМ) представляют собой устройство, предназначенное для выполнения вычислительных операции по заданной программе.

Современная электронная вычислительная машина – это сложнейший комплекс устройств, восхищающий своим технологическим совершенством и разнообразием физических принципов работы.

Вычислительные машины в зависимости от способа представления информации подразделяются на две большие группы: вычислительные машины непрерывного действия, или аналоговые вычислительные машины (АВМ), и вычислительные машины дискретного действия, или цифровые вычислительные машины (ЦВМ).

В АВМ входные, выходные и промежуточные величины представляются в виде токов или напряжений, значения которых в определенном масштабе соответствуют числом.

Математические действия над числами заменяются в АВМ различными преобразованиями электрических токов или напряжений.

Подлинный прогресс науки, называемой математической логикой, был достигнут в середине XIX в. Прежде всего благодаря труду английского логика Джорджа Буля «Математический анализ логики». Он перенес на логику законы и правила алгебраических действий, ввел логические операции, предложил способ записи высказываний в символической форме.

Современная математизированная формальная логика представляет собой обширную научную область и находит широкое применение как внутри математики (исследование оснований математики), так и вне ее (анализ и синтез автоматических устройств, теоретическая кибернетика, в частности, искусственный интеллект).

Формы мышления. Первые учения о формах и способах рассуждений возникли в странах Древнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные древнегреческими мыслителями. Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления (речи) от его содержания.

---

Логика- это наука о формах и способах мышления.

Законы логики отражают в сознании человека свойства, связи и отношения объектов окружающего мира. Логика позволяет строить формальные модели окружающего мира, отвлекаясь от содержательной стороны.

Мышление всегда осуществляется в каких-то формах. Основными формами мышления являются понятие, высказывание и умозаключение.

Понятие выделяет существенные признаки объекта, которые отличают его от других объектов. Объекты, объединенные понятием, образуют некоторое множество. Например, понятие «компьютер» объединяет множество электронных устройств, которые предназначены для обработки информации и обладают монитором и клавиатурой. Даже по этому короткому описанию компьютер трудно спутать с другими объектами, например с механизмами, служащими для перемещения по дорогам и хранящимися в гаражах, которые объединяются понятием «автомобиль».

Понятие- это форма мышления, фиксирующая основные, существенные признаки объекта. Понятие имеет две стороны: содержание и объем. Содержания понятия составляет совокупность существенных признаков объекта. Чтобы раскрыть содержание понятия, следует найти признаки, необходимые и достаточные для выделения данного объекта из множества других объектов. Свое понимание окружающего мира человек формулирует в форме высказываний (суждений, утверждений). Высказывание строится на основе понятий и по форме является повествовательным предложением. Высказывание может быть ложным или истинным. Истинным будет высказывание, в котором связь понятий правильно отражает свойства и отношение реальных вещей. Ложным высказывание будет в том случае, когда оно не соответствует реальной действительности.

Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо ложно, либо истинно.

Умозаключение. Умозаключения позволяют на основе известных фактов, выраженных в форме суждений (высказываний), получать заключение, то есть новое знание. Примером могут быть геометрические доказательства.

Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение).

Алгебра логики (раздел высказываний) – раздел математической логики, изучающий строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.

В алгебре логики над высказываниями можно производить различные операции (подобно тому в алгебре чисел определены операции сложения, деления, возведения в степень над действительными числами).

Обозначать высказывания будем прописными буквами. Если высказывание А истинное, то будем писать «А=1» и говорить «А истинно». Если высказывание А ложное, то будем писать «А=0» и говорить «А ложно».

---

Для структурно-функционального описания логических схем, составляющих основу любого дискретного вычислительного устройства, ЭВМ или ВС в целом, используется аппарат булевой алгебры, созданной в 1854 г. Дж. Булем как попытка изучения логики мышления математическими методами. Впервые практическое применение булевой алгебры было сделано К. Шенноном в 1938 г. для анализа и разработки релейных переключательных сетей, результатом чего явилась разработка метода представления любой сети, состоящей из совокупности переключателей и реле, математическими выражениями и принципов их преобразования на основе правил булевой алгебры. Ввиду наличия аналогий между релейными и современными электронными схемами аппарат булевой алгебры нашел широкое применение для анализа, описания и проектирования последних. Использование булевой алгебры позволяет не только более удобно оперировать с булевыми выражениями (представляющими те или иные электронные узлы), чем над схемами или логическими диаграммами, но и на формальном уровне путем эквивалентных преобразований и базовых теорем упрощать их, давая возможность создавать экономически и технически более совершенные электронные устройства любого назначения. Являясь основным средством анализа, разработки и описания структурно-функциональной архитектуры современной ВТ, булева алгебра является обязательной составной частью курса “компьютерной информатики”, а также целого ряда разделов вычислительных наук.

Логические основы ЭВМ

Рассмотрим, как применяется алгебра высказываний при конструировании устройств.

Чтобы конструировать устройство, мы должны знать:

• Каким образом следует реализовать логические значения 0 и 1 в виде электрических сигналов на входе и выходе устройства;

• Каким образом описать работу этого устройства:

• Существует ли алгоритм, позволяющий по известной таблице истинности построить схему устройства;

• Из каких элементов должно состоять устройство.

Постановка подобных вопросов и поиск ответов на них привели к построению простейших преобразователей информации, составляющих основу любой вычислительной машины.

Цифровой сигнал - это сигнал, который может принимать только одно из двух установленных значений.

Физическая природа сигнала может быть самой различной. Сигналами могут считаться, например, появление на выходе преобразователя напряжения или давления воздуха определенной величины, включение лампы или звонка, нажатие кнопки, срабатывание электромагнитного реле и другие изменения в электрической цепи. При этом обязательно надо, чтобы имелось два существенно различных состояния некоторой физической величины, моделирующие истинность и ложность логических высказываний.

Логическим элементом называется преобразователь, который, получая сигналы об истинности отдельных высказываний, обрабатывает их и в результате выдает значение логического отрицания, логической суммы или логического произведения этих высказываний.

---

Логические функции и логические элементы

ЦВМ состоит из отдельных элементов, выполняющих элементарные операции, Элемент-это обычно электронная схема. Все элементы ЦВМ разделить на группы в зависимости от значения этих элементов: логические, запоминающие, усилительные и специальные.

Из логических элементов создают операционные схемы, которые обеспечивают арифметические и иные операции. Название «логический элемент» обусловлено тем, что отдельный элемент позволяет осуществить определенную связь или как принято говорить, выполнить отдельную логическую функцию. Рассмотрим некоторые наиболее существенные функции и логические элементы, реализующие их.

1. Логическая функция «И»

Конъюнкцию (объединение) - логическая функция «И». Два (или более) высказывания могут быть объединены в одно сложное.

Конъюнкцию называют логической функцией «И». Обозначим истинное высказывание единицей (1), а ложное нулем (0).

Конъюнкцию двух высказываний обозначим знаком «&» или «».

Конъюнкцию двух высказываний можно записать по правилам логического умножения.

Графическое изображение: Таблица истинности

Вход		Выход
Х1	Х2	У
0	0	0
0	1	0
1	0	0
1	1	1

Уравнение логического элемента «И»: У=Х1Х2

Логический элемент И выполняет действие умножение.

2. Логическая функция «ИЛИ»

Дизъюнкция (разъединение) – логическая функция «ИЛИ».

Дизъюнкцией назовем сложное высказывание, которое истинно при истинности хотя бы одного из составляющих его высказываний, и ложно, если оба высказывания, которые образуют сложное.

Дизъюнкцию обозначается знаком «+», который читается «ИЛИ». Дизъюнкция двух высказываний может быть записана по правилам логического сложения.

Графическое изображение:

Вход		Выход
Х1	Х2	У
0	0	0
0	1	1
1	0	1
1	1	1

Уравнение логического элемента «ИЛИ»: У=Х1 V Х2

Логический элемент ИЛИ выполняет действие сложение.

3. Логическая функция «НЕ»

Это связь означает отрицание истинности, присущей какому-либо высказыванию. Символически логическая функция НЕ обозначается чертой над символом заданного высказывания: (читается не «Х»).

Логический элемент, реализующий логическую функцию НЕ, называется инвертором.

Таблица истинности

Вход	Выход
Х	У
0	1
1	0

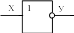
Уравнение логического элемента «НЕ»: У=

Логические функции и логические элементы Буль алгебра.

Бульевский (логический) типы. Boolean имеет два значения – TRUE (истинно) и FALSE (ложно). Над значениями допустимы операции сравнения, причем считается, что false (фалс)< true(тру) значения булевского типа занимают один байт памяти. В версии Turbo Pascal 7.0 добавлены еще три булевских типа: ButeBool, WordBoll, LongBool для обеспечения совместимости с WINDOWS.

---