Файл: петербургский государственный университет путей сообщения министерства путей сообщения российской федерации.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 30.11.2023

Просмотров: 86

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Государственное образовательное учреждение высшего профессионального образования


«ПЕТЕРБУРГСКИЙ

ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ


МИНИСТЕРСТВА ПУТЕЙ СООБЩЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ»



Кафедра «Автоматика и телемеханика на железных дорогах»



СТРУКТУРНЫЙ МЕТОД РАСЧЕТА НАДЕЖНОСТИ

Методические указания

к выполнению практической работы по дисциплине: «Надежность CЖАТ»

САНКТ-ПЕТЕРБУРГ 2007

2

1 Структурная схема расчета надежности

Структурнаясхемарасчетанадежности(ССРН)-этографическоепредставление условий, при которых объект находится в работоспособномилинеработоспособном состоянии.Элементы, из которых состоит ССРН, означают события, которые мо-гут произойти (с точки зрения надежности) с элементами исследуемого объ-екта.Например, элемент электрической схемы - резистор может быть в ра-ботоспособном состоянии (событие А) или неработоспособном состоянии(событие В). В неработоспособное состояние он может перейти в результатеобрыва(событие1)иликороткого замыкания(событие2)резистора.Элементы ССРН могут включаться последовательно или параллельно.Последовательноонисоединяются,есликаждоесобытие(например,1или2) ведет к отказу объекта. Параллельно элементы ССРН соединяются в слу-чаях, когда к отказу объекта ведет совместное наступление всех событий,учитываемых при расчетенадежности.
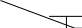
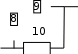
Численные значения параметров надежности объекта могут быть оп-ределены,еслизаменитьсобытия,учтенныеприанализеивошедшиевССРН,на вероятности этихсобытий.ЭлементыССРНмогутобразовыватьпростыеисложныеузлы.Простой узел образуется из одного или k - элементов включенных па-раллельно(наРис.1это узлы,образованныеэлементами4-5иэлементом6).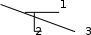

Рис.1Сложные узлы образуются из параллельно-последовательного соеди-нения, в котором в одной из параллельных ветвей последовательно включе-но несколько элементов (узел, образованный элементами 1 - 2 - 3 на Рис.1)Расчет надежности сложного узла выполняется, начиная с последовательно-го соединения элементов. В рассматриваемом примере необходимо найтинадежность ветви с последовательным соединением элементов 2 - 3, а затемнадежностьпараллельногосоединения элементов1и2–3.
1-2-3

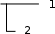
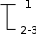
Рис.2.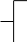Заканчивается преобразование структурной схемы после полученияэквивалентногозначениянадежностивсехпоследовательновключенныхузлов.
1-2-3
4-5
6-7-8-9-10

1-2-3-4-5-6-7-8-9-10
j-оепреобразование1узел 2узел 3узел объектРис.3.В результате j преобразований необходимо получить аналитическоевыражениерасчетанадежностисистемы позаданнойССРН.
 
Если в узле имеется структура типа мостика (структура из элементов 6, 7, 8, 9, 10 на Рис. 1), то для преобразования в последовательно- параллельную схему используют формулу разложения по ключевому эле- менту: F(a,b,c,...)aF(1,b,c,...)aF(0,b,c,...)На основании этой формулы можно сформулировать следующее об-щееправило разложения общейструктурыпоключевомуэлементу:

  1. В исходной структуре выбирается элемент с наибольшим числом связей – элемент разложения х.

  2. В месте расположения элемента х делается замыкание. Получается первая структура. Последовательно перед ней включается элемент разложе- ния х.

  3. В месте расположения элемента х в исходной структуре делается обрыв. Получается вторая структура. Последовательно перед ней включает- ся элемент x.

  4. Исходная структура эквивалентна параллельному включению по- лученных выше структур.
Рассмотрим разложение по ключевому элементу структуры из эле-ментов 6, 7, 8, 9, 10 на Рис. 1. В качестве элемента разложения используемэлементмостика–8.Тогдаисходнаяструктурапреобразуетсяквиду: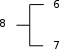

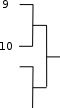
2 Параметры надежности

Интенсивность отказа - условная плотность вероятности возникнове-нияотказаневосстанавливаемогообъекта,определяемаяприусловии,чтодо рассматриваемого момента времени отказ не возникнет- вобщем слу-чаеопределяетсяпоформуле

 (t)  

P' (t)



P(t)

f(t)


P(t)

(1)


где f(t)—плотность распределения наработки до отказа,

Р(t)– вероятность безотказной работы.


  c
 Например, для систем с общим резервированием, состоящих из n рав- нонадежных элементов с экспоненциальным законом распределения, интен- сивность отказов определяется выражением

c(t)

P' (t)

net(1 et)n1




(2)



Pc(t)

1 (1 e t)n

где  - интенсивность отказов одного элемента,

Рс(t),Р'с(t)– вероятность безотказной работы резервированной систе- мы и ее производная.

Cредняя наработка до отказа определяется по формуле



Tо P(t)dt

0

(3)

Для случая экспоненциального закона распределения времени безот- казной работы, вероятность безотказной работы определяется как:

P(t)  e t

Вероятность отказа Q(t)равна

Q(t)  1 P(t)  1 et

(4)
(5)


  1. Расчет вероятности безотказной работы для невосстанавливаемых элементов, соединенных последовательно



Вероятность безотказной работы узла P(t), состоящего из nпоследо- вательно включенных элементов равна:

Py(t) 


p1 (t)  p2 (t) ... pn(t)  pi(t)

i1

, (6)

где Py(t)- вероятность безотказной работы узла,

pi(t)- вероятность безотказной работы i-го элемента.

Для случая экспоненциального закона распределения времени безот- казной работы:

nPy(t) 
eit


ti

ei1

eyt
(7)


n где

y ii1

i1

- интенсивность отказов узла (1/ч),

i (t) - интенсивность отказов i-го элемента (1/ч).

Поэтому в результате первого преобразования (см. Рис.1) получим

P2-3(t)=P2(t)P3(t)=e-(2 3 )t

Вероятность отказа узла Qy(t) равна

(8)

Qy(t)= 1 -Py(t) (9)

  1. Расчет вероятности безотказной работы для невосстанавливаемых элементов, соединенных параллельно



Вероятность безотказной работы узла, состоящего из mпараллельно включенных элементов равна

Py(t) =1 -Qy(t), (10)

где Qy(t)- вероятность отказа узла.

Используя теорему об умножении вероятностей, получим

Qy(t)=q1(t)q2(t)…qm(t) =[1-p1(t)][1-p2(t)]…[1-pm(t)], (11) где qi(t) =1 - pi(t)- вероятность отказа i-го элемента.

Для двух элементов, соединенных параллельно, получим:

Py(t) =1-([1- p1(t)][1-p2(t)])= p1(t) +p2(t)-p1(t)p2(t), (12)

Например, вероятность безотказной работы узла (см. Рис.2) найдем после второго преобразования

P1-2-3( t )=p1(t) +p23(t) -p1(t)p23(t) (13)

Смотрите также файлы