Файл: В таблице имеются данные об общей численности пенсионеров рф в исследуемые годы.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 150
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание 1В таблице имеются данные об общей численности пенсионеров РФ в исследуемые годы.
Используя данные таблицы 3, выполните задания:1. Определите вид статистического ряда, представленного в таблице.2. По данным таблицы определите основные показатели динамики.3. Определите среднюю численность пенсионеров в исследуемый период. Обоснуйте применённую Вами формулу.4. По данным таблицы постройте динамический график численности пенсионеров в исследуемый период.-----------------------------------------------------------------1. Статистического ряд, представленный в таблице представляет собой ряд динамики.2. По данным таблицы определите основные показатели динамики.Важнейшим статистическим показателем анализа динамики является абсолютный прирост (сокращение), т.е. абсолютное изменение, характеризующее увеличение или уменьшение уровня ряда за определенный промежуток времени. Абсолютный прирост с переменной базой называют скоростью роста.Абсолютные приросты вычисляются по формулам: (цепной) (базисный)где yi — уровень сравниваемого периода; yi-1— уровень предшествующего периода; У0 — уровень базисного периода.Для оценки интенсивности, т. е. относительного изменения уровня динамического ряда за какой-либо период времени исчисляют темпы роста (снижения).Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному.Показатель интенсивности изменения уровня ряда, выраженный в долях единицы, называется коэффициентом роста,
3. Определим среднюю численность пенсионеров в исследуемый период. Средний уровень интервального ряда с разностоящими уровнями вычисляется по формуле средней арифметической взвешенной: (тыс.чел.)4. По данным таблицы постройте динамический график численности пенсионеров в исследуемый период.Рис. 4. Динамический график численности пенсионеров в исследуемый период5. Постройте парную линейную регрессию численности пенсионеров в исследуемый период.Х – номер года; Y – численность пенсионеровДля расчета параметров а и b линейной регрессии решаем систему нормальных уравнений относительно а и b:Из системы коэффициенты линейной регрессии a и b определяются по формулам:Расчеты оформим в таблице:Таблица 4
Уравнение парной линейную регрессии численности пенсионеров определяется формулой:6. Используя построенную модель регрессии, сделаем прогноз на 2010 годДанные о численности пенсионеров в 2010 году взяты из статистического сборника «Российский статистический ежегодник» — Стат.сб./Росстат. — М., 2011.Численность пенсионеров в 2010 году составляла 39706 тыс. чел.Прогноз численности пенсионеров на основе полученной модели составляет: (тыс.чел.)Сравним прогнозные данные с реальной ситуацией: реальная численность пенсионеров в 2010 году превышает численность, полученную при расчете по уравнению парной регрессии, на 2,15% или 834 тыс. чел.Задача по выборочному наблюдениюПроведено выборочное тестирование студентов факультета по экономическим дисциплинам. Численность факультета 850 студентов, объем выборки, сформированной методом бесповторного отбора — 24 студента. Результаты тестирования приведены в таблице. По этим данным определить выборочные средний балл, дисперсию и стандартное отклонение. Вычислить ошибку выборки, найти границы доверительного интервала, в котором окажется средняя генеральной совокупности с вероятностью 0,866 и 0,997.
| год | 1995 | 2000 | 2005 | 2007 | 2008 |
| Численность пенсионеров (тыс. чел.) | 37083 | 38411 | 38313 | 38467 | 38598 |
а в процентах — темпом роста. Эти показатели интенсивности изменения отличаются только единицами измерения.
Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число.
Коэффициент роста вычисляются по формулам:
(цепной)
(базисный)
Темпы роста:
(цепной)
(базисный)
Темпы прироста:
(цепной)
(базисный)
Абсолютное значение одного процента прироста Ai . Этот показатель служит косвенной мерой базисного уровня. Представляет собой одну сотую часть базисного уровня, но одновременно представляет собой и отношение абсолютного прироста к соответствующему темпу роста.
Данный показатель рассчитывают по формуле
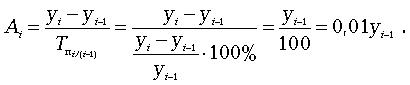
Расчеты показателей оформим в таблице.
Таблица 3
| Годы | Численность пенсионеров, тыс. чел. | Абсолютные приросты, тыс. чел. | Коэффициенты роста | Темпы роста, % | Темп прироста, % | Абсолютное содержание 1% прироста, тыс. чел. | ||||
| цеп | баз | цеп | баз | цеп | баз | цеп | баз | |||
| 1995 | 37083 | — | — | — | — | — | — | — | — | — |
| 2000 | 38411 | 1328 | 1328 | 1,0358 | 1,0358 | 103,58 | 103,58 | 3,58 | 3,58 | 370,83 |
| 2005 | 38313 | -98 | 1230 | 0,9974 | 1,0332 | 99,74 | 103,32 | -0,26 | 3,32 | 384,11 |
| 2007 | 38467 | 154 | 1384 | 1,0040 | 1,0373 | 100,40 | 103,73 | 0,40 | 3,73 | 383,13 |
| 2008 | 38598 | 131 | 1515 | 1,0034 | 1,0409 | 100,34 | 104,09 | 0,34 | 4,09 | 384,67 |
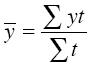
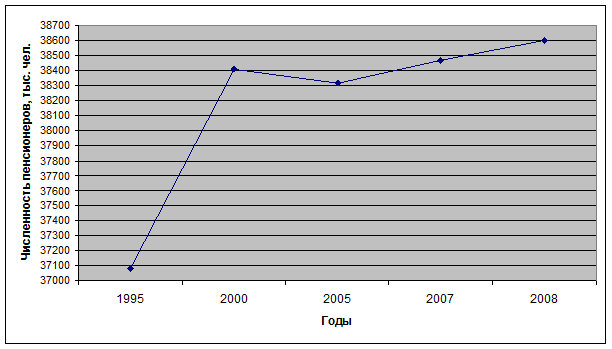
3. Определим среднюю численность пенсионеров в исследуемый период. Средний уровень интервального ряда с разностоящими уровнями вычисляется по формуле средней арифметической взвешенной: (тыс.чел.)4. По данным таблицы постройте динамический график численности пенсионеров в исследуемый период.Рис. 4. Динамический график численности пенсионеров в исследуемый период5. 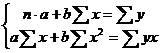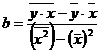Постройте парную линейную регрессию численности пенсионеров в исследуемый период.Х – номер года; Y – численность пенсионеровДля расчета параметров а и b линейной регрессии решаем систему нормальных уравнений относительно а и b:Из системы коэффициенты линейной регрессии a и b определяются по формулам:Расчеты оформим в таблице:Таблица 4
| № п/п | Х | Y | ХY | X2 |
| 1 | 1995 | 37083 | 73980585 | 3980025 |
| 2 | 2000 | 38411 | 76822000 | 4000000 |
| 3 | 2005 | 38313 | 76817565 | 4020025 |
| 4 | 2007 | 38467 | 77203269 | 4028049 |
| 5 | 2008 | 38598 | 77504784 | 4032064 |
| Итого | 10015 | 190872 | 382328203 | 20060163 |
| Среднее значение | 2003 | 38174,4 | 76465640,6 | 4012033 |
Уравнение парной линейную регрессии численности пенсионеров определяется формулой:6. Используя построенную модель регрессии, сделаем прогноз на 2010 годДанные о численности пенсионеров в 2010 году взяты из статистического сборника «Российский статистический ежегодник» — Стат.сб./Росстат. — М., 2011.Численность пенсионеров в 2010 году составляла 39706 тыс. чел.Прогноз численности пенсионеров на основе полученной модели составляет: (тыс.чел.)Сравним прогнозные данные с реальной ситуацией: реальная численность пенсионеров в 2010 году превышает численность, полученную при расчете по уравнению парной регрессии, на 2,15% или 834 тыс. чел.Задача по выборочному наблюдениюПроведено выборочное тестирование студентов факультета по экономическим дисциплинам. Численность факультета 850 студентов, объем выборки, сформированной методом бесповторного отбора — 24 студента. Результаты тестирования приведены в таблице. По этим данным определить выборочные средний балл, дисперсию и стандартное отклонение. Вычислить ошибку выборки, найти границы доверительного интервала, в котором окажется средняя генеральной совокупности с вероятностью 0,866 и 0,997.
| № п/п | Оценка (в баллах) | № п/п | Оценка (в баллах) | № п/п | Оценка (в баллах) | № п/п | Оценка (в баллах) | |||||||||||
| 1 | | 112 | 7 | | 105 | | 13 | | 98 | | 19 | 95 | | |||||
| 2 | | 95 | 8 | | 108 | | 14 | | 95 | | 20 | 115 | | |||||
| 3 | | 119 | 9 | | 110 | | 15 | | 111 | | 21 | 94 | | |||||
| 4 | | 98 | 10 | | 101 | | 16 | | 115 | | 22 | 105 | | |||||
| 5 6 | | 112 95 | 11 12 | | 117 99 | | 17 18 | | 130 104 | | 23 24 | 121 111 | | |||||