Файл: Анализ структуры и уровня заболеваемости. Определим интенсивный показатель для каждого исследуемого год.docx

Ⅰ. Анализ структуры и уровня заболеваемости.1. Определим интенсивный показатель для каждого исследуемого года – заболеваемость, отражающую частоту заболеваний, рассчитанную на 100 тысяч населения (‱)Таблица 1.1

Год	Абсолютное число	Показатель на 100 тыс.	Численность населения
2012	60	5,15	3214065
2013	393	33,69	3211931
2014	58	4,95	3212676
2015	128	10,92	3209325
2016	658	56,15	3203679
2017	487	41,59	3193514
2018	525	44,88	3192416
2019	442	37,99	3183038
2020	269	23,26	3179532
2021	1	0,09	3172925
2022	267	23,32	3164384
Итого: n=11	3288	281,99	3194316,82

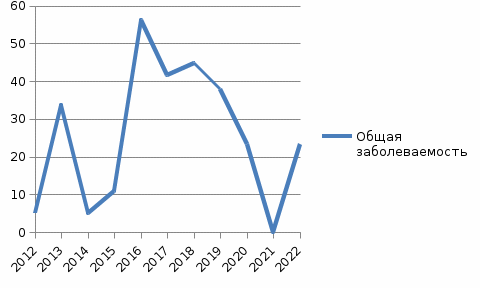
Построим график заболеваемости населения Гриппом в Самарской области с 2012 по 2022 гг.Рис 1.1 Заболеваемость совокупного населения в Самарской области с 2012 по 2022 гг.2. Рассчитаем ошибку (m) интенсивного показателя по формуле:±m=√p(100000-p)/n, Где p - уровень заболеваемости (на 100 000)n - численность населенияСоставим таблицу:Таблица 1.2. Расчет ошибки интенсивного показателя.

Год	Показатель на 100 тыс. населения	Численность населения	Ошибка интенсивного показателя (±m)
2012	5,15	3214065	0,4
2013	33,69	3211931	1,02
2014	4,95	3212676	0,4
2015	10,92	3209325	0,6
2016	56,15	3203679	1,3
2017	41,59	3193514	1,1
2018	44,88	3192416	1,2
2019	37,99	3183038	1,1
2020	23,26	3179532	0,8
2021	0,09	3172925	0,05
2022	23,32	3164384	0,8
Итого: 11	281,99	Средняя численность населения=3194316,82	8,75

---

3. Рассчитаем среднюю величину.Наиболее часто для расчета средней величины используется среднее арифметическое – Xср. Рассчитаем среднюю величину заболеваемости населения Гриппом для характеристики исследуемой совокупности в целом одним числом.Xср = ∑Y/n,Где Y – значение каждого наблюдения (показатель заболеваемости);n – число наблюдений Составим вариационный ряд – показатели заболеваемости, расположенные в порядке нарастания величины ( в верхнем ряду – показатели заболеваемости, в нижнем ряду – соответствующий год)Таблица 1.3. Вариационный ряд.

0,09	4,95	5,15	10,92	23,26	23,32	33,69	37,99	41,59	44,88	56,15
2021	2014	2012	2015	2020	2022	2013	2019	2017	2018	2016

Из вариационного ряда видно число наблюдений – 11Xср=281,99/11= 25,6Для оценки достоверности средней величины необходимо рассчитать ошибку средней величины (±m) по формуле: ±m=δ/√n,где, δ - среднее квадратичное отклонение, характеризующее разброс значений вариационного ряда около среднего значения, рассчитывается по формуле (если число наблюдений менее 30):δ=√∑(X-Xср)²/(n-1),где X – значение вариант, из которых состоит ряд (показатели заболеваемости);Xср – среднее значение ряда;n – число анализируемых лет.Составим таблицу:Таблица 1.4.

Год	X (заболеваемость)	(x-xср)²
2012	5,15	418,2
2013	33,69	65,4
2014	4,95	426,4
2015	10,92	215,5
2016	56,15	933,3
2017	41,59	255,6
2018	44,88	371,7
2019	37,99	153,5
2020	23,26	5,4
2021	0,09	650,7
2022	23,32	5,2
Итого: 11	218,99	3500,9

---

δ = √∑(x-xср)²/(n-1)=18,7±m = δ/√n=5,63Средняя величина является достаточно точной, статистически достоверной, если она превосходит свою ошибку не менее чем в 2 раза.4. Сравним показатели заболеваемости текущего года со средними показателями предшествовавших лет.Заполним таблицу:Таблица 1.5.

	Среднегодовые показатели предшествующих лет			Показатели отчетного года (2022г)			Рост/снижение
	Абс.ч	На 100000	%		Абс.ч	На 100000
Грипп	298,90	281,99			267	23,32		Снижение в 1,1 раза

Показатели заболеваемости Гриппом отчетного года меньше в 1,1 раза по сравнению со среднегодовыми показателями заболеваемости предшествующих лет.Определим достоверность различий с помощью критерия Стьюдента (t):t = │y-yср│/√m²+m²ср.где y – показатель заболеваемости отчетного года;yср – средний показатель заболеваемости предшествующих лет;m – ошибка показателя отчетного года;mср – ошибка среднего показателя предшествующих лет.При расчете показателя заболеваемости на 100 000 населения (‱0)m = √y(100000–y)/nгде n – численность населения отчетного года;mср = √y(100000 – yср)/nср;где nср – средняя численность населения предшествующих летm = √23,32 (100000 – 23,32)/3164384 = 0,8mср = √281,99 (100000 – 281,99)/3194316,82 = 2,9t = 23,32-281,99/√0,8+2,9² = 86Доверительная вероятность считается достаточной, если она равна 95,5% и более (p ≤ 0,5).По таблице значений доверительной вероятности найдем значение t, равное P= 95,5 и более, из таблицы tтаб. = 2 и более.Сравним критерий Стьюдента из таблицы с рассчитанным критерием Стьюдента: 86 > 2,2881, следовательно, показатели заболеваемости Гриппом отчетного года (2022) достоверно ниже среднемноголетних показателей за 11 предшествующих лет.

---

2. Анализ многолетней динамики заболеваемости.Задачи:

1. 
   получить графическое изображение динамики заболеваемости по календарным годам;
   
2. 
   определить тенденцию многолетней динамики заболеваемости;
   
3. 
   оценить уровень заболеваемости в текущем году;
   
4. 
   определить цикличность эпидемического процесса;
   
5. 
   провести краткосрочное прогнозирование уровня заболеваемости на следующий год;
   
6. 
   выявить скрытые вспышки, если таковые имеются.
   

2.1 Определение тенденции многолетней динамики заболеваемостиМноголетняя динамика заболеваемости формируется под влиянием постоянных, периодических и случайно действующих факторов. Выявим тенденции заболеваемости Гриппом за изучаемый период времени, периодичность эпидемического процесса в многолетней динамике и апериодические колебания заболеваемости.Чтобы устранить или уменьшить влияние нерегулярных, причин на динамику заболеваемости, выделить и изучить особенности заболеваемости, которые формируются под воздействием постоянных или периодических факторов, проводим преобразование динамического ряда показателей заболеваемости.Табл 2.1. Многолетняя динамика заболеваемости совокупного населения Гриппом в Самарской области с 2012 по 2022гг.

Год	Показатель на 100 000 населения ‱0	Численность населения
2012	5,15	3214065
2013	33,69	3211931
2014	4,95	3212676
2015	10,92	3209325
2016	56,15	3203679
2017	41,59	3193514
2018	44,88	3192416
2019	37,99	3183038
2020	23,26	3179532
2021	0,09	3172925
2022	23,32	3164384

---

2.1. Определение прямолинейной тенденции многолетней динамики заболеваемости методом наименьших квадратов.Выявление резко отличающихся величин в динамическом ряду. Необходимость исследования динамических рядов с целью выявления и замены резко отличающихся показателей заболеваемости связано с тем, что такие показатели формируются, как правило, под действием случайных факторов, не характерны для основной части совокупности и могут привести к существенным искажениям многолетней тенденции заболеваемости. Показатели ранжируются, крайние члены ряда проверяются по критерию Шовене на “выскакивающие величины”. С этой целью рассчитывается средний многолетний показатель заболеваемости по формуле:Yср = ∑Yi/n,где Yi– показатель заболеваемости для каждого года,n – число лет исследования.Yср = 281,99/11 = 26Расчет отклонений показателей заболеваемости от среднемноголетнего уровня, квадрат отклонений по формулам:(Y1-Yср); (Y1-Yср)²; ∑(Y1-Yср)²Данные заносятся в таблицу.Табл. 2.2.

Год	Yi-(заболеваемость), ‱0	Ранги	Yi-Yср	(Yi-Yср)
2012	5,15	3	-20,85	429,5
2013	33,69	7	7,69	59,1
2014	4,95	2	-21,05	443,1
2015	10,92	4	-15,08	227,4
2016	56,15	11	30,15	909,02
2017	41,59	9	15,59	243,04
2018	44,88	10	18,88	356,4
2019	37,99	8	11,99	143,7
2020	23,26	5	-2,74	7,5
2021	0,09	1	-21,91	480,04
2022	23,32	6	-2,68	7,1
Итого:	281,99		15,99	3305,9

---