Файл: Анализ структуры и уровня заболеваемости. Определим интенсивный показатель для каждого исследуемого год.docx

Рассчитывается среднее квадратическое отклонение (δ) и ошибка (m) по формуле:

δ = √3305,9/11 = 17,3, и
Показатели прямолинейной тенденции вычисляются по формуле Y1 = a + bx.

а – среднемноголетний уровень заболеваемости,

m = δ√n-1 = 17,3/3,1=5,5

Табл. 2.3. Исходные материалы для изучения многолетней динамики заболеваемости Гриппом в Самарской области.

Годы	Показатель заболеваемости Yi, ‱0	X	X²	X⁴	Yi*X	YiX²	Y1	Y2	Отклонение Y1-Y2
2012	5,15	-5	25	625	-25,75	128,75	23,6	48,6	-25
2013	33,69	-4	16	256	-134,76	539,04	24	49	-25
2014	4,95	-3	9	81	-14,85	44,55	24,4	49,4	-25
2015	10,92	-2	4	16	-21,84	43,68	24,8	49,8	-25
2016	56,15	-1	1	1	-56,15	56,15	25,2	50,2	-25
2017	41,59	0	0	0	0	0	0	0	0
2018	44,88	1	1	1	44,88	44,88	26	51	-25
2019	37,99	2	4	16	75,98	151,96	26,4	51,4	-25
2020	23,26	3	9	81	69,78	209,34	26,8	51,8	-25
2021	0,09	4	16	256	0,36	1,44	27,2	52,2	-25
2022	23,32	5	25	625	116,6	583	27,6	52,6	-25
Итого:	281,99		∑= 110		∑= 54,24

---

Далее проверяют крайние значения (max, min) ряда.

Kmax = Ymax-Yср/δ

Кmax = (56,15-26)/17,3=1,7

Сравниваем полученную величину с критерием Шовене для n=11: по таблице коэф.=2,26.

Так как Kmax больше табличного коэффициента 2,26, то это “выскакивающая” величина. Учитывая, небольшой анализируемый ряд (11 лет), “выскакивающий” показатель заменим теоретическим, вычисленным по формуле для замены максимальных показателей:

Kmin=Ymin-Yср/δ

Kmin=(0,09-26)/17,3= -1,4

Сравниваем полученную величину с критерием Шовене для n=11: по таблице коэф.=2,26

Поскольку Kmin не превышает табличного коэффициента, то минимальное значение заболеваемости не является выскакивающей величиной.
bx – переменная величина, формирующая прямолинейную тенденцию.

X – условная нумерация периодов (лет)

a = ∑Y/n = 25,6

b = ∑Yi*X/∑X² = 0,4
Полученные результаты заполняются в таблицу.
Таблица 2.3.

Годы	a +	b *	x	bx	a+bx
2012	25,6	0,4	-5	-2	23,6
2013	25,6	0,4	-4	-1,6	24
2014	25,6	0,4	-3	-1,2	24,4
2015	25,6	0,4	-2	-0,8	24,8
2016	25,6	0,4	-1	-0,4	25,2
2017	25,6	0,4	0	0	25,6
2018	25,6	0,4	1	0,4	26
2019	25,6	0,4	2	0,8	26,4
2020	25,6	0,4	3	1,2	26,8
2021	25,6	0,4	4	1,6	27,2
2022	25,6	0,4	5	2	27,6

---

Полученные показатели наносят на график: многолетняя динамика заболеваемости Гриппом в Самарской области 2012-2022 гг.

(выравнивание по функции y=a+bx)



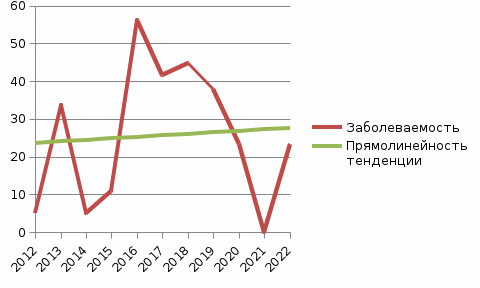
Рис 2.1. Заболеваемость Гриппом населения Самарской области за период 2012 – 2022 гг. Прямолинейная тенденция заболеваемости.


Определяется общая направленность тенденции. Таким образом, при выравнивании динамического ряда методом наименьших квадратов выявляется тенденция к повышению заболеваемости.
Вычисление криволинейной тенденции заболеваемости.

Показатели криволинейной тенденции вычисляются по формуле

Y2 = a+bx+cx²

Получаем уравнение с 2-мя неизвестными:

Y₂ = 25,6 + (0,4*x) + cx²
Y₂ = 25,6+(0,4 *(-5) +25c
Y₂= 25,6 + (-2)+25с
Y₂ = 23,6 + 25c
23,6 = y - 25c
y = 9,5 + 25c
Определение выраженности тенденции

Определяем средний абсолютный прирост, который характеризует среднюю величину ежегодного прироста или снижения заболеваемости по формуле:

Δ = Yn – Y1 / n – 1;

Yn - показатель заболеваемости последнего года,

Y1 – показатель заболеваемости первого года,

n – число анализируемых лет.

Δ = 23,32 – 5,15/10=1,8

Рассчитываем среднемноголетний темп прироста (T пр.ср) для прямолинейной тенденции:

Tпр.=B * 100%/A,

где B- величина, на которую ежегодно идет прирост или снижение заболеваемости;

A – среднемноголетний показатель заболеваемости.

Tпр. = 1,8 * 100/25,6 = 7
Оценивается выраженность тенденции по следующим критериям:

Tпр.ср. от 0 до ±1% - заболеваемость стабильна.

Tпр.ср. от ±1 до ±5% - тенденция динамики заболеваемости умеренная (средневыраженная),

Tпр.ср. ≥ ±5% - тенденция выраженная.

Вывод: выраженность тенденции к повышению заболеваемости Гриппом в Самарской области за период 2012-2022 гг умеренная или средневыраженная.
Сглаживание динамического ряда для оценки цикличности.

Устранение действия случайных факторов методом укрупнения периодов

Объединяем несколько смежных годов (2,3,4, и т.д.), рассчитываем для них среднюю величину заболеваемости по формуле:

Yср =Y1 + Y2 + Y3 /3

Полученные значения заносим в таблицу (2.4) и строим график (2.2)
Преобразование динамического ряда методом скользящей средней:

---

точки теоретической линии также определяются как средние арифметические из показателей нескольких смежных лет, но каждый показатель учитывается при расчете нескольких средних. Например, при скользящем осреднении с шагом 3 года, скользящие средние определяются по формулам:

Yср1 =Y1 + Y2 + Y3 /3; Yср2 =Y1 + Y2 + Y3 /3

На графике полученные значения откладываем, соответственно, напротив 2-го и 3-го года. Когда период осреднения включает четное число лет, скользящие средние относят к середине интервала между двумя центральными годами.

Полученные данные вносим в таблицу (2.4) и строим график (2.3)
Таблица 2.4.

Годы	Заболеваемость %000	Заболеваемость при преобразовании динамического ряда,%000
		Методом укрупнения периодов	Методом скользящей средней
2012	5,15	14,5
2013	33,69		14,5
2014	4,95		16,5
2015	10,92	38,3	24
2016	56,15		36,2
2017	41,59		47,5
2018	44,88		41,4
2019	37,99	21,1	35,3
2020	23,26		20,4
2021	0,09		15,5
2022	23,32

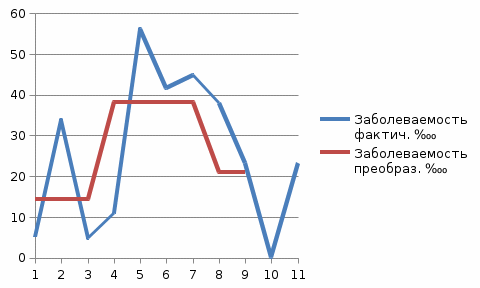
Рис. 2.2. Заболеваемость при преобразовании динамического ряда методом укрупнения периодов.


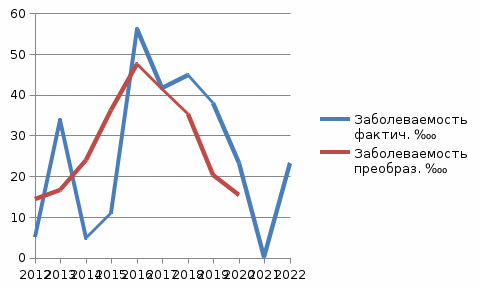
Рис. 2.3. Заболеваемость при преобразовании динамического ряда методом скользящей средней.
Выводы: При преобразовании динамического ряда заболеваемости населения Гриппом методом укрупнения периодов и методом скользящей средней, на графиках преобразованные линии заболеваемости имеют такие же периоды снижения и повышения заболеваемости совокупного населения Гриппом Самарской области, как и на графике заболеваемости населения в динамике за период с 2012 по 2022 гг, и имеют 2 периода повышения заболеваемости: 2012 г. по 2013 г., и с 2014 г. по 2016 г; и 2 периода снижения заболеваемости: с 2017 г. по 2019 г., и с 2020 г. по 2022 г. с тенденцией к стабилизации заболеваемости.

---

2.2 Определение цикличности эпидемического процесса

Проводится на основании оценки соотношения кривой фактической заболеваемости и прямолинейной тенденции. Определение эпидемических и межэпидемических лет в анализируемом периоде, т.е. цикличности в течение эпидемического процесса. Определяется разность между фактической заболеваемостью (Yфакт.) и теоретический (Yт.), рассчитанной для каждого года.

Проводится выравнивание динамического ряда методом скользящей средней полученной разности по анализируемому ряду с шагом 2 года т.е,

Y₁ = (Y факт 2000 - Y r2000) + (Y факт.2001 - Y +2001) /2
Y₂= (Y факт 2001 - Y (2001) + (Y факт 2002 - Y +2002) /2


Данные заносятся в таблицу.

Таблица 2.5.

Годы	Заболеваемость фактическая, Yфакт. ‱0	Заболеваемость теоретическая, Yт. ‱0	Заболеваемость Yфакт. - Yт. , ‱0	Выравнивание дин.ряда методом скользящей средней
2012	5,15	23,6	-18,45	14,07
2013	33,69	24	9,69	-4,88
2014	4,95	24,4	-19,45	-16,6
2015	10,92	24,8	-13,88	8,5
2016	56,15	25,2	30,95	36,2
2017	41,59	0	41,59	30,2
2018	44,88	26	18,88	15,2
2019	37,99	26,4	11,59	8,05
2020	23,26	26,8	-3,54	-15,3
2021	0,09	27,2	-27,11	-15,6
2022	23,32	27,6	-4,28	-31,39

---