Список литературы

1. Седов. В.М, Гайнутдинов Т.А. Электромагнитные поля и волны. – М. Горячая линия Телеком, 2017. с. 210 – 238.

2. Пименов Ю.В., Вольман В.И., Муравцов А.Д. Техническая электродинамика. – М: Радио и Связь, 2000. с. 360 – 388, с. 401 – 407.

3. Сазонов Д.М. Антенны и устройства СВЧ. – М. Высшая школа. 1988. с. 36 – 47.

ПРИЛОЖЕНИЯ
П.1 ЭКВИВАЛЕНТНОЕ СОПРОТИВЛЕНИЕ ЛИНИИ И ФОРМУЛА ТРАНСФОРМАЦИИ

При анализе процессов, происходящих в линиях передачи конечной длины, обычно пользуются методами теории длинных линий, основанных на концепции падающих и отраженных волн. Структура каждой, отдельной падающей или отраженной волны предполагается такой же, как в линии бесконечной длины. Напряжение и ток в длинной линии рассматриваются соответственно как суммы напряжений и токов падающей и отраженной волны

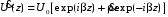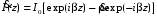, , (1)

где 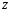- расстояние от конца линии (нагрузки) до исследуемого сечения лини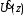и, и 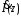-комплексные амплитуды напряжения и тока в исследуемом сечени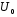и, и 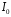- амплитуды напряжения и тока в падающей волне, 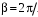λ- коэффициент фазы, λ- длина волны в линии, 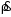- коэффициент отражения по напряжению.

Отношение амплитуд напряжения и тока в бегущей (падающей) волне равно волновому сопротивлению линии 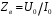. Отношение комплексных амплитуд напряжения и тока в сечении линии 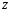называют эквивалентным сопротивление линии 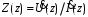. Эквивалентное сопротивление линии 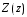имеет ясный физический смысл. Если обрезать линию в сечении z (от генератора до сечения с координатой z) и нагрузить оставшуюся часть линии на сопротивление нагрузки численно равное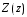

---

, то распределение амплитуд напряжения и тока в оставшейся части линии останется таким же как и до обрезания. Эквивалентное сопротивление, вычисленное для сечения, соответствующего входу линии ( 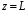) называют входным сопротивлением линии 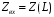, где 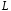- длина линии. В конце линии (в сечении нагрузки 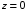) эквивалентное сопротивление равно сопротивлению нагрузки 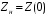. Очевидно, что эквивалентное сопротивление линии в сечении равно входному сопротивлению отрезка линии длиной , нагруженного на сопротивление .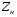

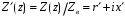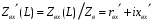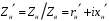Отношение эквивалентного сопротивления к волновому сопротивлению называют нормированным эквивалентным сопротивлением линии . Соответственно величины и называют нормированным входным сопротивлением линии и нормированным сопротивление нагрузки. Помимо нормированных сопротивлений используют и нормированные проводимости. Нормированная эквивалентная проводимость линии определяется как 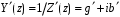. Нормированная входная проводимость линии и нормированная проводимость нагрузки определяются аналогично ,

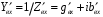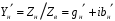
Волновод является одним из видов линии передачи, поэтому полученные в теории длинных линий результаты можно использовать и при рассмотрении волноводов. Во многих случаях, особенно связанных с оценкой эффективности переноса мощности электромагнитного поля по волноводу, оказывается удобным вместо волновода рассматривать эквивалентную ему двухпроводную длинную линию [1, 2].

В волноводной технике стараются пользоваться только нормированными сопротивлениями и проводимостями [1-3]. Из теории длинных линий [1-3] известна формулы, связывающая между собой нормированное эквивалентное сопротивление (проводимость) в сечении

---

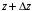с нормированным эквивалентным сопротивлением (проводимостью) в сечении

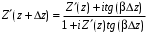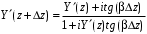, . (2)

Формулы (2) показывают как трансформируется эквивалентное сопротивление (проводимость) вдоль длинной линии, поэтому эти формулы принято называть формулами трансформации. Частным случаем формул трансформации (формул пересчета) является ситуация, когда в качестве начального сечения выбирается сечение нагрузки 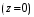, и формулы (2) приобретают вид

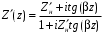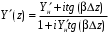, . (3)

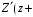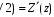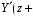Из (2) видно, что λ , λ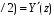 . Отсюда следует, что эквивалентные нормированные сопротивления (проводимости) являются периодическими функциями продольной координаты с периодом λ/2, поэтому для полного описания трансформации эквивалентных сопротивлений (проводимостей) вдоль длинной линии достаточно определить эти величины на любом удобном интервале длиной λ/2. Эквивалентные сопротивления (проводимости) связаны с величиной коэффициента отражения и КБВ следующими соотношениями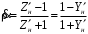

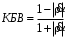, . (4)
П.2 КРУГОВАЯ ДИАГРАММА ПОЛНЫХ СОПРОТИВЛЕНИЙ И ОПРЕДЕЛЕНИЕ СОПРОТИВЛЕНИЯ НАГРУЗКИ

Сравнительно высокая трудоемкость вычислений по формулам (2) и (4), необходимых для определения энергетической эффективности процесса переноса мощности по линии передачи привела к созданию специального устройства, необходимого для упрощения расчетов по (2), (4) при сохранении приемлемой с инженерной точки зрения точности. Данное устройство получило название круговая диаграмма полных сопротивлений (диаграмма Вольперта-Смита). В дальнейшем мы не будем использовать термин нормированные сопротивления и проводимости, а просто говорить о сопротивлениях и проводимостях, поскольку круговая диаграмма используют только нормированные величины. Общий вид диаграммы приведен на рисунке 11, а вид в масштабе, достаточном для проведения практических расчетов, в литературе [2, 3].

---

---

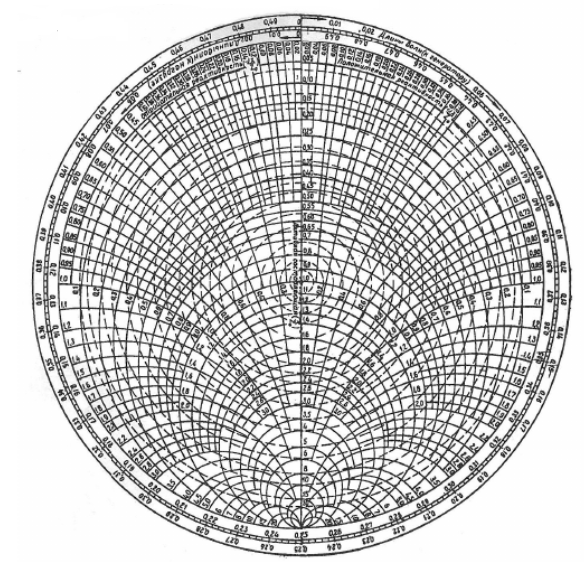
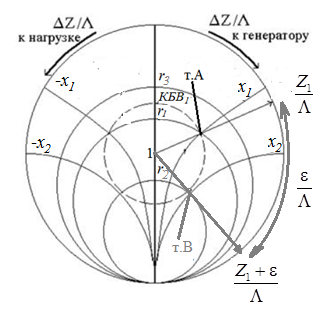
Рисунок 11 Рисунок 12

На круговой диаграмме полных сопротивлений нанесено три семейства кривых, внешняя окружность с указанием направления пересчета и один вертикальный отрезок (см. рисунок 11, а также литературу [2, 3]). Для большей наглядности на рисунке 12 приведены некоторые из этих семейств:

1. 
   Вертикальный отрезок чисто активных сопротивлений (проводимостей) (x=0). На этом отрезке в логарифмическом масштабе откладываются числа, причем центром отрезка (центром круговой диаграммы) является число 1, верхнем концом отрезка 0, а нижнем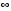 . В нашем примере, изображенном на рисунке 12 на этом отрезке отложены четыре числа r_1, r_2, КБВ_1, r₃
   
2. 
   Семейство сплошных окружностей r=const с центрами на вертикальной оси. Эти окружности получили названия окружности равных активных сопротивлений (проводимостей). Любая точка, лежащая на этой окружности, имеет постоянное активное сопротивление (проводимость). На рисунке 12 указаны три таких окружности с постоянным сопротивлением r_1, r_2, r_3.
   
3. 
   Семейство пунктирных окружностей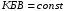 с центром в середине вертикального отрезка чисто активных сопротивлений. Эти окружности получили название окружностей равного КБВ. Любая точка, лежащая на этой окружности, имеет постоянный КБВ. На рисунке 12. указана одна из этих окружностей с КБВ=КБВ₁. Для определения величины этого КБВ достаточно найти координату пересечения этой окружности с верхней частью вертикального отрезка. Координата пересечения окружности постоянного КБВ с нижней частью вертикального отрезка определяет величину коэффициента стоячей волны (КСВ), который равен 1/КБВ.
   
4. 
   Семейство дуг окружностей x=const, имеющих общую точку в нижнем конце вертикального отрезка. Эти дуги получили название дуги равных реактивных сопротивлений (проводимостей). Любая точка, лежащая на этой дуге, имеет постоянное реактивное сопротивление (проводимость). Дуги, соответствующие положительным значениям x находятся справа от отрезка чисто активных сопротивлений, а дуги, соответствующие отрицательным значениям x слева. На рисунке 12 представлены две дуги с положительным реактивным сопротивлением х_1, x₂, и две дуги с отрицательными реактивными сопротивлениями -х_1,-x₂ . Для определения конкретной величины реактивного сопротивления дуги необходимо определить координату пересечения дуги с внешним кругом круговой диаграммы.
   
5. 
   Внешняя окружность, по которой откладывается расстояние пересчета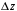 сопротивлений (проводимостей) и направление пересчета (к генератору по часовой стрелке, к нагрузке против часовой стрелки, как показано на рисунке 12). Так как круговая диаграмма используется для пересчета сопротивлений (проводимостей) для различных линий, работающих в разных частотных диапазонах, величины начальной координаты и расстояние пересчета 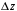на круговой диаграмме указывается в долях длины волны в лини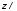и λ и 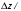λ. Верхняя точка внешней окружности располагается в верхнем конце вертикального отрезка и соответствует нормированной координате 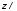λ=0, нижняя точка внешней окружности совпадает с нижним концом вертикального отрезка и соответствует координате 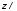λ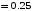 . После перехода через нижнюю точку окружности пересчета идет дальнейший рост нормированной координаты и по достижению полного круга координата проходит путь 0.5λ, что вытекает из свойств периодичности эквивалентного сопротивления (проводимости).
   

---

Смотрите также файлы

• Муниципальное бюджетное общеобразовательное учреждение xxxxxxx.docx

• Концептуальные основы проектирования в работе с семьей и детьми.docx

• Помощь студентам, готовые работы для Вуза httpsstudwork orginfo147162.pdf

• 1. Саки. Территория их расселения. Хозяйство, общественное устройство и культура.docx

• 6сынып.docx