Файл: Лабораторная работа 1 Испытание стальных образцов на разрыв.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 26
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа № 1
Испытание стальных образцов на разрыв
Цель работы: исследовать зависимость удлинения образца от значения растягивающего усилия вплоть до разрыва и определить механические характеристики материала ( пределы пропорциональности, упругости, текучести и прочности, относительное удлинение и сужение.
Проведение эксперимента.
-
Измерим штангенциркулем диаметр с точностью до 0,1 мм в трех местах по длине образца. За окончательный результат примем наименьшее значение. Вынесем рисками на образец расчетную длину l0=10d. -
Найдем площадь поперечного сечение с расчетной части образца. -
Заложим в захваты машины образец, настроим записывающее устройство и произведем растяжение образца с последующим разрывом. -
Со шкалы силоизмерителя запишем значения Р.
Обработка результатов измерений.
-
Полученные значения Р нанесем на диаграмму растяжения. -
Измерим длину расчетной части образца, вычислим остаточную деформацию и нанесем ее на диаграмму растяжения. -
Вычислим механические характеристики. -
Измерим диаметр в месте разрыва в двух взаимно перпендикулярных направлениях и по среднему арифметическому двух значений найдем площадь поперечного сечения. -
Вычислим характеристики пластичности материала. -
Построим угловую диаграмму напряжений в осях σ-ɛ. -
По результатам эксперимента заполним таблицу 1.
| Ма те ри ал | Размеры образца, мм | ????l, мм | Pпц, кН | Pу, кН | Pт, кН | Pв, кН | σпц, МПа | σу, МПа | σт, МПа | σв, МПа | |||||||||||
| до опыта | после опыта | ||||||||||||||||||||
| l0 | d0 | l1 | d1 | ||||||||||||||||||
| | 120 | 12 | 168 | 7 | 50 | 22,8 | 23,5 | 24,0 | 38,7 | 201,7 | 208,3 | 212,3 | 342,2 | ||||||||
Таблица 1
Расчетные формулы:
Расчетная длина до испытания:
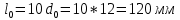
Площадь поперечного сечения с расчетной части образца:
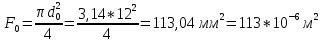
Расчетная длина после испытания:
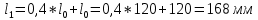
Наименьшая плотность поперечного сечения рабочей части образца после испытания:
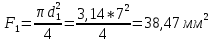
Удлинение образца после испытаний:
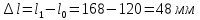
Предел пропорциональности:
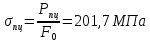
тогда:
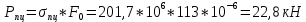
Предел упругости:
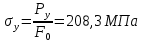
тогда:
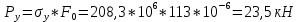
Предел текучести:
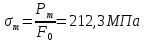
тогда:
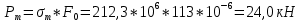
Предел прочности:
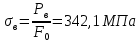
тогда:
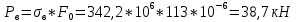
Характеристики пластичности материала:
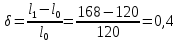
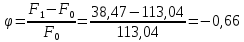
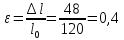
Условная диаграмма напряжений в осях σ-ɛ представлена на рисунке 1.
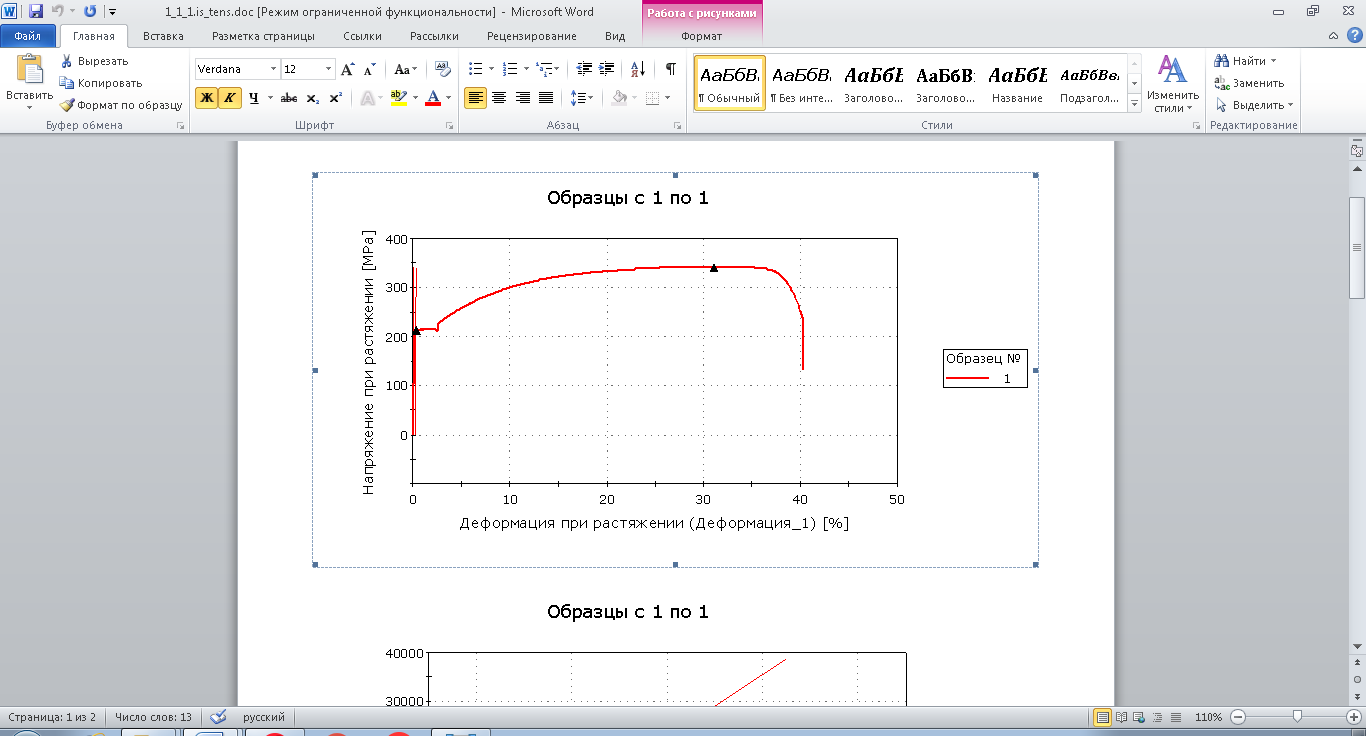
Рисунок 1
Вывод: в процессе выполнения лабораторной работы №1 была исследована зависимость удлинения образца от значения растягивающего усилия вплоть до разрыва и определены механические характеристики материала ( пределы пропорциональности, упругости, текучести и прочности, относительное удлинение и сужение), построена условная диаграмма напряжений.
Контрольные вопросы:
-
Какие характеристики отражают прочность материала?
-характеристики определяются напряжениями
, деформациями (упругими, пластическими).
-
Какие образцы применяют при испытании на разрыв?
- Испытания на разрыв (или на растяжение) осуществляют как для пластичных, так и для хрупких материалов. Для этого используют образцы разной формы - плоские или цилиндрические. По длине они также могут быть различными - короткими или длинными.
-
Какие параметры характеризуют пластичность материала?
-Пластичность характеризует относительное удлинение σ и относительное сужение ψ (его называют поперечным сужением). Удлинение - это характеристика пластичности металла, оцениваемая по увеличению длины образца из этого металла при растяжении.
-
Чем отличается диаграмма истинных напряжений от диаграммы условных напряжений?
-Диаграмма растяжения в осях Р-????l является по существу характеристикой образца из данного материала, так как при одном и то же значении силы Р величина удлинения зависит от поперечных и продольных размеров образца. Чтобы исключить влияние размеров образца и получить характеристику материала, диаграмму растяжения строят в координатах σ-ɛ.
-
Как определить по диаграмме упругую и пластическую деформацию?
-упругая деформация при растяжении переходит в зону текучести (или пластическую деформацию).