Файл: Лабораторная работа по курсу "Общая физика" изучение спектра атома водорода г. Томск 2012.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 30.11.2023

Просмотров: 30

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


Федеральное Агентство по образованию
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра физики

ОТЧЕТ

Лабораторная работа по курсу "Общая физика"

ИЗУЧЕНИЕ СПЕКТРА АТОМА ВОДОРОДА

г.Томск 2012

1. ЦЕЛЬ РАБОТЫ
Целью работы является изучение спектра излучения атомов водорода и экспериментальное определение постоянной Ридберга.
2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА
Для изучения спектра атома водорода используется спектроскоп на основе призменного монохроматора УМ-2. Схема экспериментальной установки приведена на рис.2.1.



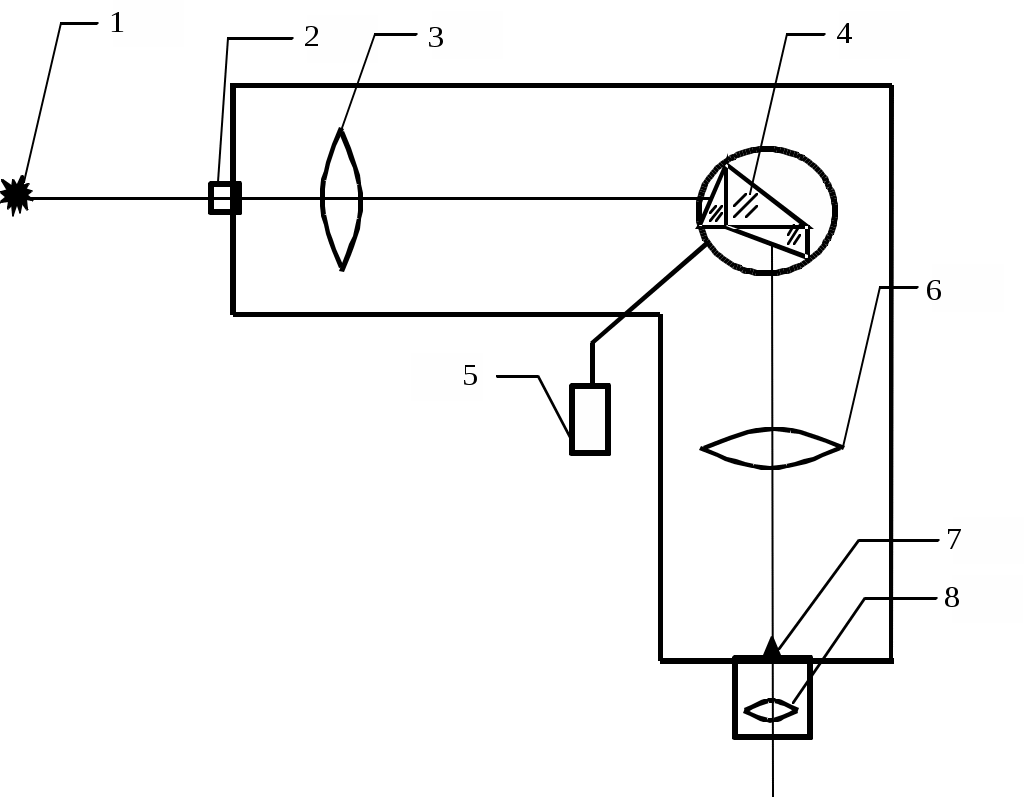
1 – источник света, 2 – входная щель спектроскопа, 3 – входной объектив, 4 – сложная спектральная призма, 5 – микрометрический винт с отсчетным барабаном, 6 – входной объектив, 7 – указатель, 8 - окуляр

Рис.2.1 Схема экспериментальной установки
Свет от источника 1 через входную щель 2 и объектив 3 параллельным пучком падает на спектральную призму с высокой дисперсией 4. Призмой свет разлагается в спектр и через объектив 6 направляется в окуляр 8. При повороте призмы в центре поля зрения появляются различные участки спектра. Призму поворачивают при помощи барабана 5, на которой нанесена шкала в градусах. Вращением барабана спектральную линию подводят к стрелке указателя 7, расположенного в окуляре, и фиксируют отсчет по шкале барабана.

Источником света в данной работе являются газоразрядная водородная трубка и ртутная лампа высокого давления ДРШ-250-3.
3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
Постоянная Ридберга (угловой коэффициент), расчёт по графику:

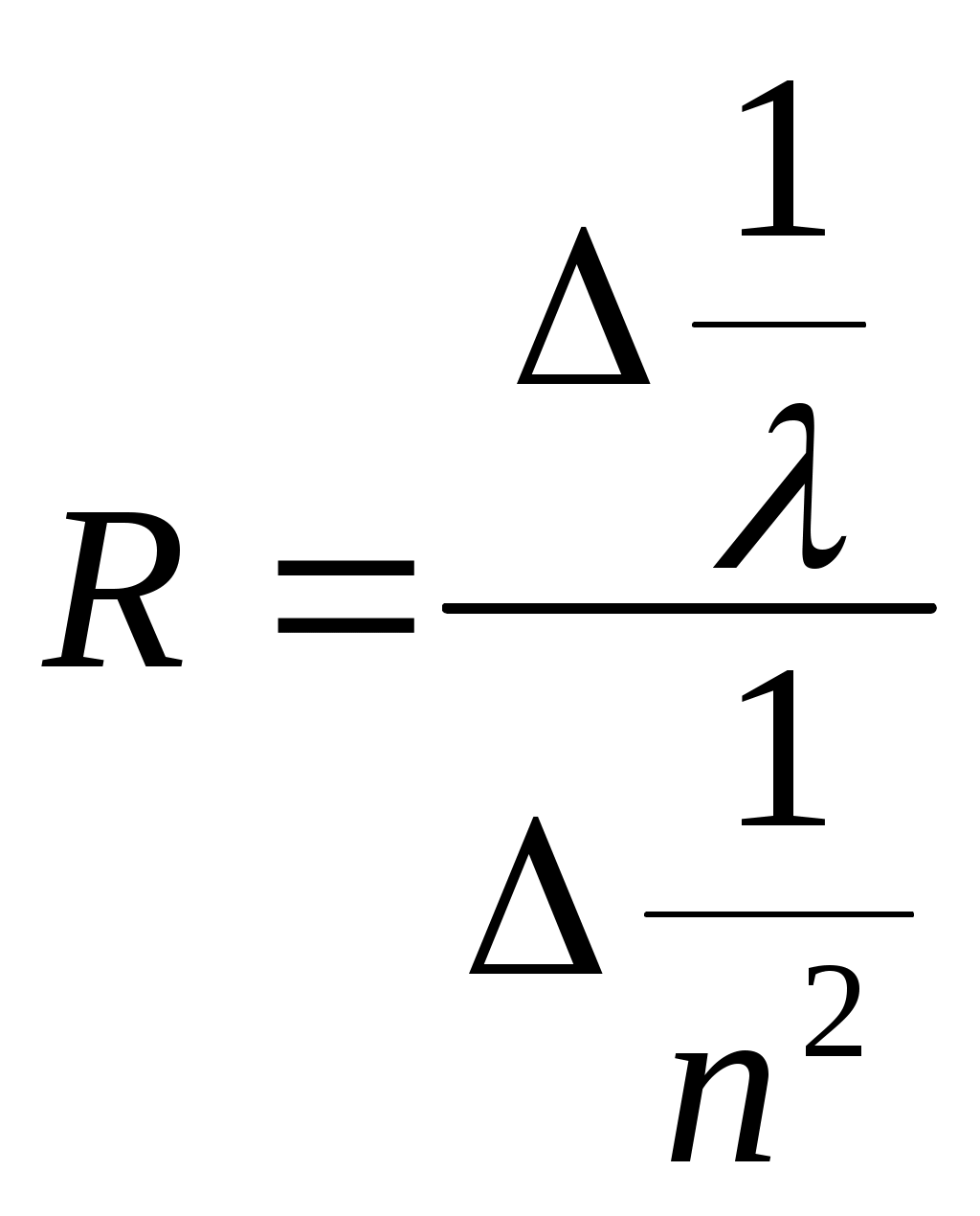, где (3.1)

λ – длина волны спектральных линий;

n – главное квантовое число.
Вспомогательные формулы для расчёта абсолютной погрешности постоянной Ридберга:

(3.2)

(3.3)

(3.4)

(3.5)

(3.6)

(3.7)

(3.8)

Угловой коэффициент прямой k= n*S3-S1S2/D (3.9)

Абсолютная погрешность постоянной Ридберга, как абсолютная погрешность углового коэффициента прямой k:

, где (3.10)

n – количество точек.
4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.

Таблица 4.1 – Данные градуировки спектроскопа по спектру ртути


Линия (цвет)
, град
, нм

1 фиолетовая 1

2 фиолетовая 2

3 синяя

4 голубая

5 зеленая

6 желтая 1

7 желтая 2

8 красная 1

9 красная 2
557

627

1115

1775

2194

2375

2396

2587

2828
404.7

407.8

435.8

491.6

546.1

577.0

579.1

623.4

690.7


Построим градуировочный график φ(λ).




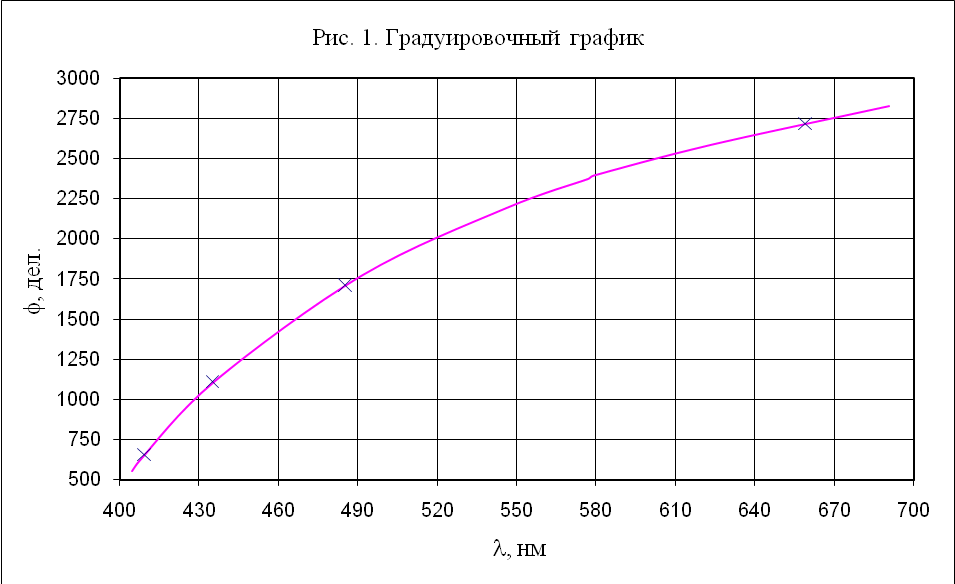
Значения длин волн λ спектральных линий водорода определяются по градуировочному графику: на оси Y откладываются значения φ, а соответствующие им значения на оси X подбираются так, чтобы точка совпала с линией. Используя график, определяем значения длин волн линий спектра водорода. Данные заносим в таблицу 4.2.

Таблица 4.2 – Экспериментальные данные спектра атома водорода


Линия (цвет)
, град
, нм

1 фиолетовая 1

2 фиолетовая 2

3 голубая

4 красная

658

1112

1712

2717
409

435

485

659


Проверим справедливость формулы Бальмера. Для этого нужно построить график зависимости 1/λ(1/n2). Рассчитываем необходимые данные, заносим в таблицу 4.3.


Таблица 4.3 – Данные для построения зависимости 1/λ(1/n2)


1/, мкм1
2,445
2,299
2,062
1,517

n*
6
5
4
3

1/n2
0,028
0,040
0,063
0,111


Построим график линейной зависимости 1/λ(1/n2)


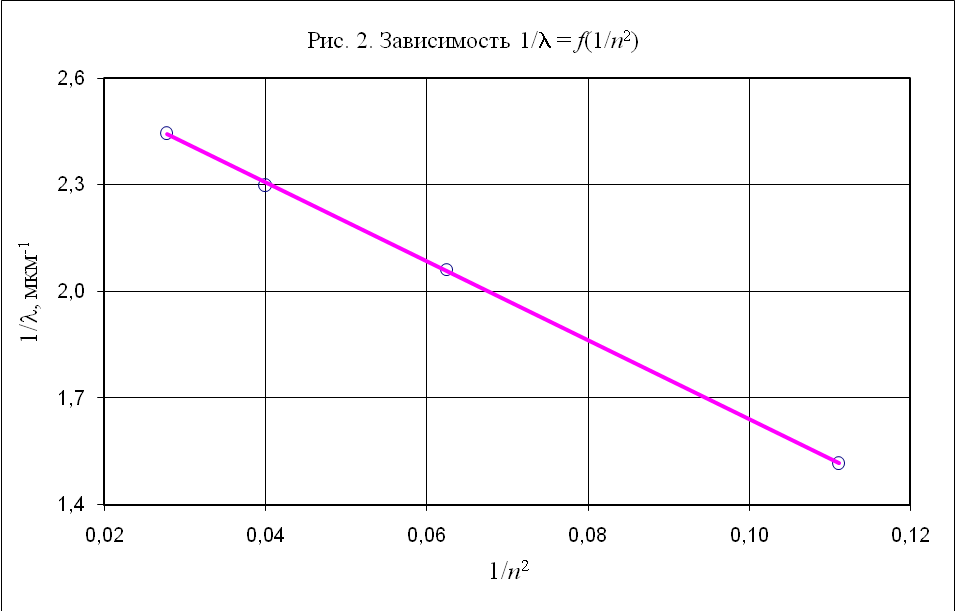
Из графика определяем постоянную Ридберга, как угловой коэффициент линейной зависимости 1/λ(1/n2) по формуле (3.1).
R = (2,445*10-6– 1,517*10-6)/( 0,111– 0,028) = 1,108*107 (м-1)
Оцениваем абсолютную погрешность R по формулам 3.2 – 3.10.








k= n*S3-S1S2/D=4*0.457-0.241*8.323/0.1623=1,108E+07 м1



Абсолютное значение углового коэффициента K прямой является постоянной Ридберга R = |K| =
1,108E+07
м1

Абсолютная погрешность найденной постоянной Ридберга (R) = (K) =
1,057E+05
м1

Табличное значение постоянной Ридберга Rтаб:
1,097E+07
м1

Отличие найденного и табличного значений постоянной Ридберга |1  R/Rтаб|100% =
0,98
%

Ошибка определения постоянной Ридберга составила0,98%.
Используя полученные из опыта значения длин волн построим фрагмент энергетического спектра атома водорода.


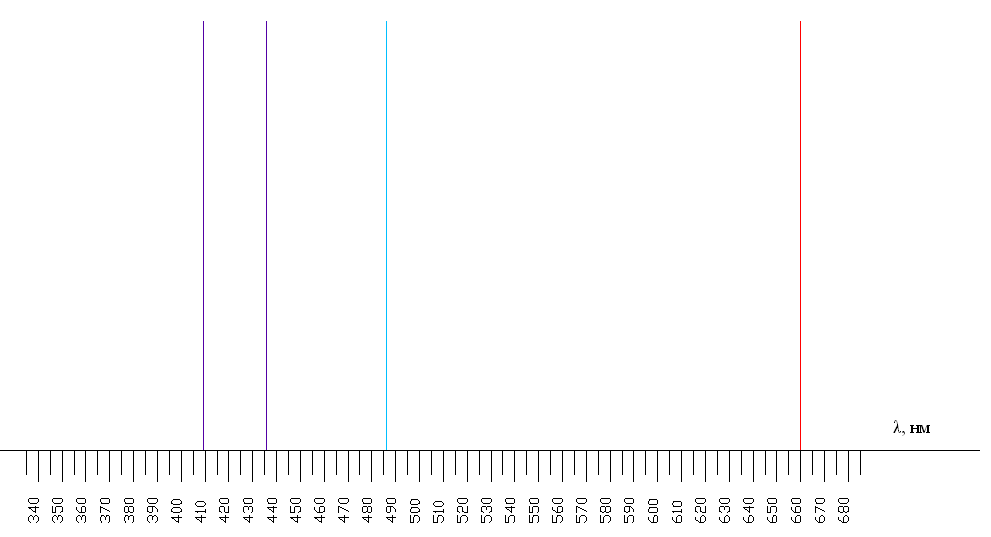
Рис. 4.3 Фрагмент энергетического спектра атома водорода
Переходы, наблюдаемые в опыте: 6s → 2p, 5s → 2p, 4s → 2p, 3s → 2p.

5. ВЫВОДЫ
В ходе лабораторной работы был изучен спектр излучения атомов водорода. Был построен график линейной зависимости 1/λ(1/n2), по которому удалось определить постоянную Ридберга (R). Погрешность экспериментального определения R составила 1,057E+05 м-1. Ошибка определения постоянной Ридберга составила 0,98%.

6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ

КОНТРОЛЬНЫЕ ВОПРОСЫ ПО ЛАБОРАТОРНОЙ РАБОТЕ №7
«ИЗУЧЕНИЕ спектра атома водорода»


  1. Объяснить принцип действия призменного спектроскопа.

Принцип действия призменного спектроскопа основан на явлении дисперсии света.


  1. В чем заключается градуировка спектроскопа?

Угол отклонения призмой лучей монохроматического света не пропорционален ни длине волны, ни его частоте. Поэтому дисперсионные спектральные приборы необходимо предварительно градуировать с помощью эталонных источников света. В данной лабораторной работе эталонным источником света являлась ртутная лампа.

Градуировка заключалась в следующем:

Установить перед входной щелью спектроскопа на расстоянии 30-40 см ртутную лампу. Включить блок питания ртутной лампы тумблерами «СЕТЬ» и «ЛАМПА ДРШ». Зажечь ртутную лампу, нажимая несколько раз на кнопку «ПУСК», и дать разогреться лампе в течение 3-5 минут. Изменяя ширину входной щели и перемещая окуляр, добиться, чтобы спектральные линии, видимые через окуляр, были тонкие и резкие.

Измерить значения угла поворота барабана для различных линий спектра ртути, совмещая последовательно линии со стрелкой указателя в окуляре. Подводить линии к указателю следует только с одной стороны, чтобы уменьшить погрешность за счет люфта барабана.



  1. Как задают состояние электрона в атоме водорода в квантовой механике?

Соответствующие энергиям En собственные функции



задают стационарные состояния электрона в атоме водорода и зависят от квантовых чисел n, l и m.

Орбитальное квантовое число l при определенном n может принимать значения l=0, 1, 2, …, n-1. Магнитное квантовое число при данном l принимает значения .


  1. Какой смысл имеет квадрат модуля волновой функции?

В соответствии с интерпретацией волновой функции квадрат модуля волновой функции дает плотность вероятности нахождения электрона в различных точках пространства.


  1. Записать стационарное уравнение Шредингера для электрона в атоме водорода.

, где

Rnl(r) – радиальная часть волновой функции;

Ylm(θ,φ) – угловая часть волновой функции;

n – главное квантовое число;

l – орбитальное квантовое число;

m – магнитное квантовое число.


  1. Привести возможные состояния для электрона в атоме водорода с n = 3.

При n = 3 возможные состояния электрона в атоме водорода: s, p, d.


  1. Что называют энергией ионизации атома водорода?

Состояние 1sатома называют основным. Ему соответствует наименьший энергетический уровень E1=-13,6 эВ, также называемый основным. Все другие состояния и энергетические уровни называются возбужденными. Величина |E1| является энергией ионизации атома водорода.


  1. Доказать, что плотность вероятности нахождения электрона на расстоянии равном боровскому радиусу является максимальной.

Вероятность обнаружения электрона в шаровом слое от r

Смотрите также файлы