Файл: Лабораторная работа по курсу "Общая физика" изучение спектра атома водорода г. Томск 2012.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 31
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
до r+dr равна объему этого слоя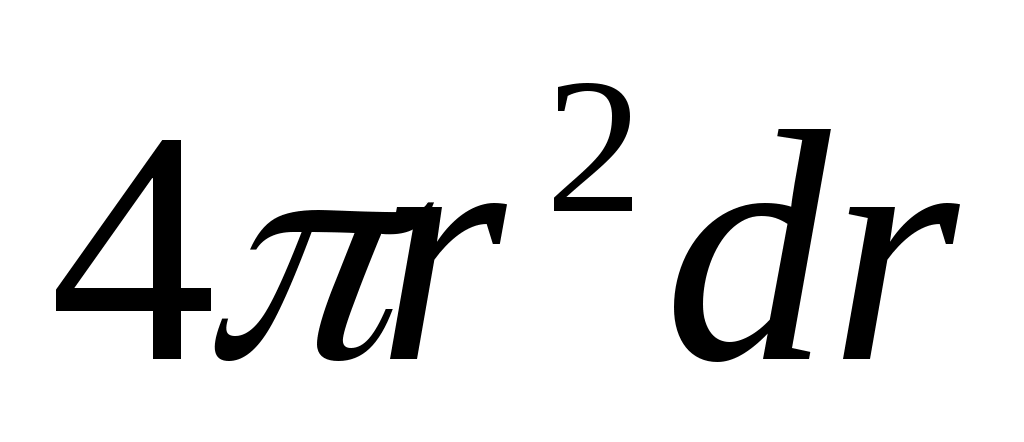
, умноженному на
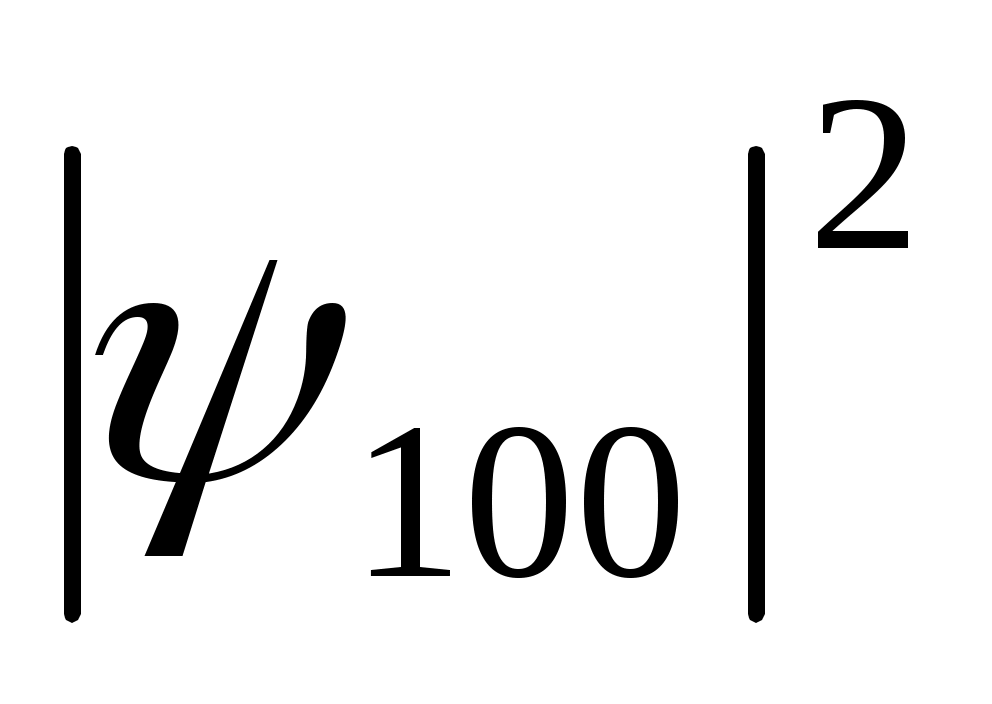. Плотность вероятности обнаружения электрона на расстоянии r от ядра
достигает максимума при r=r0.
Величина r0, имеющая размерность длины, совпадает с радиусом первой боровской орбиты. Следовательно, в квантовой механике радиус первой боровской орбиты интерпретируется как расстояние от ядра, на котором вероятность обнаружения электрона максимальна.
Из закона сохранения момента импульса при испускании и поглощении света атомом для орбитального квантового числа l возникает правило отбора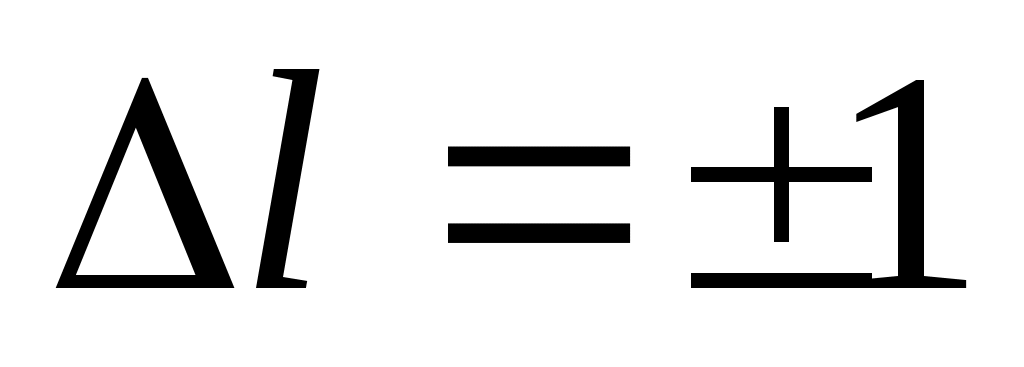
.
Для серии Лаймана: np → 1s (n = 2, 3 ...).
Для серии Пашена: np → 3s, ns → 3p, nd → 3p, np → 3d, nf → 3d (n = 4, 5 ...)
Для серии Лаймана: m = 1, n = 2, 3, … ∞.
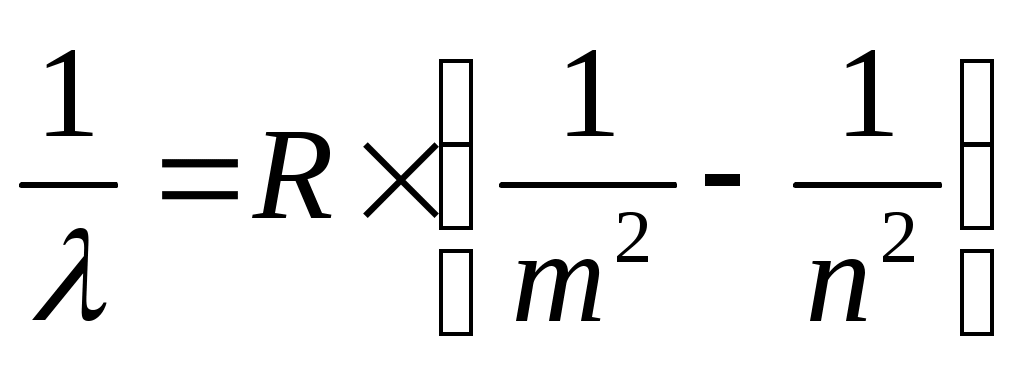, R = 1,097 ∙ 107 (м-1)
при n = ∞.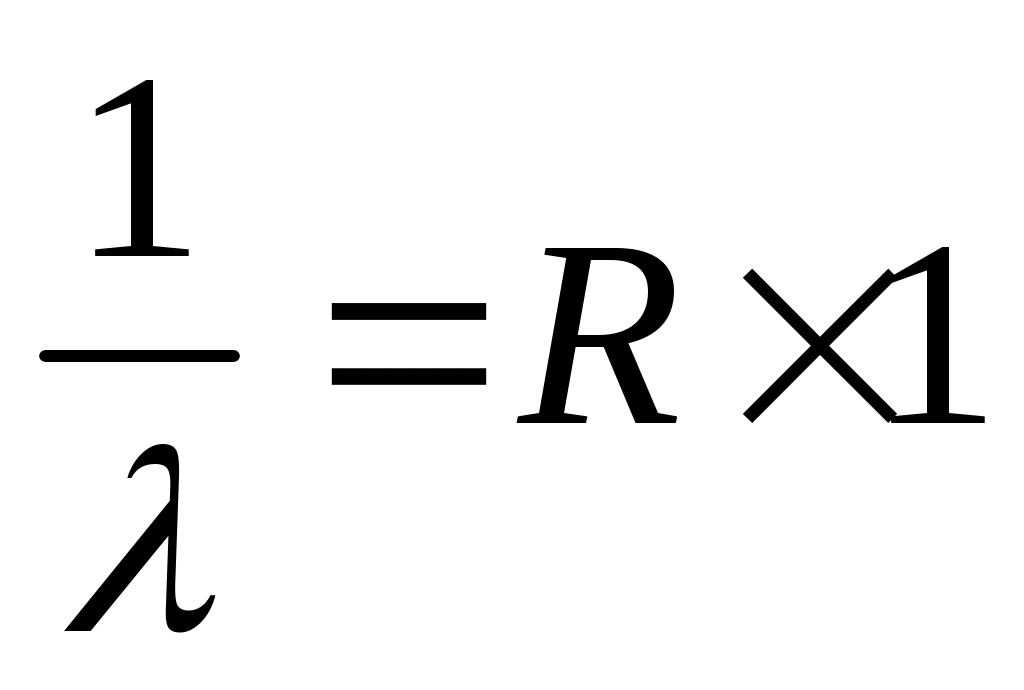
, λ1 = 1/(1,097 ∙ 107) ∙ 109 = 91,2 (нм)
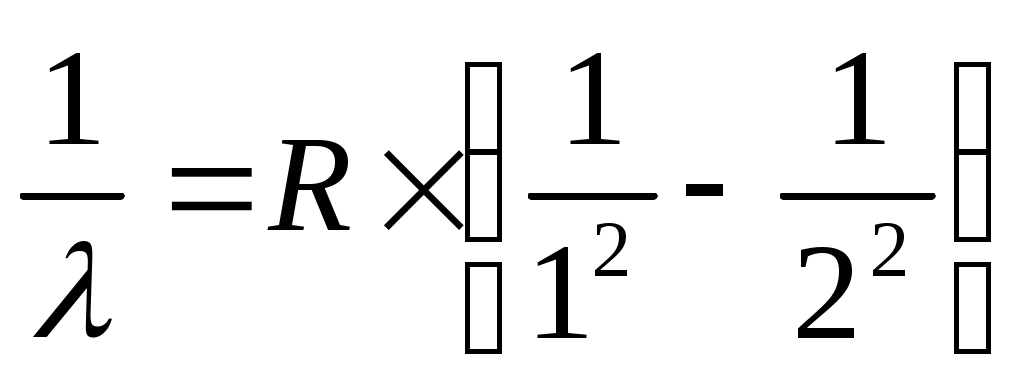, λ∞ = 1/(1,097 ∙ 107 ∙ 3/4) ∙ 109 = 121,5 (нм)
Для серии Бальмера: m = 2, n = 3, 4 … ∞.
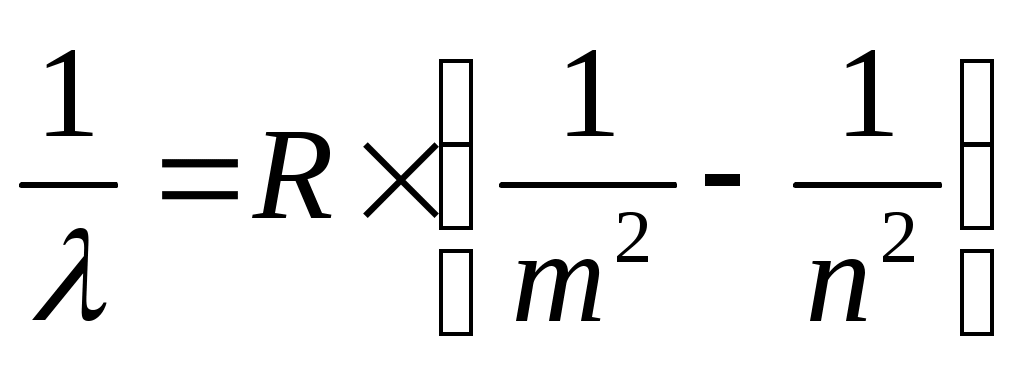, R = 1,097 ∙ 107 (м-1)
при n = ∞.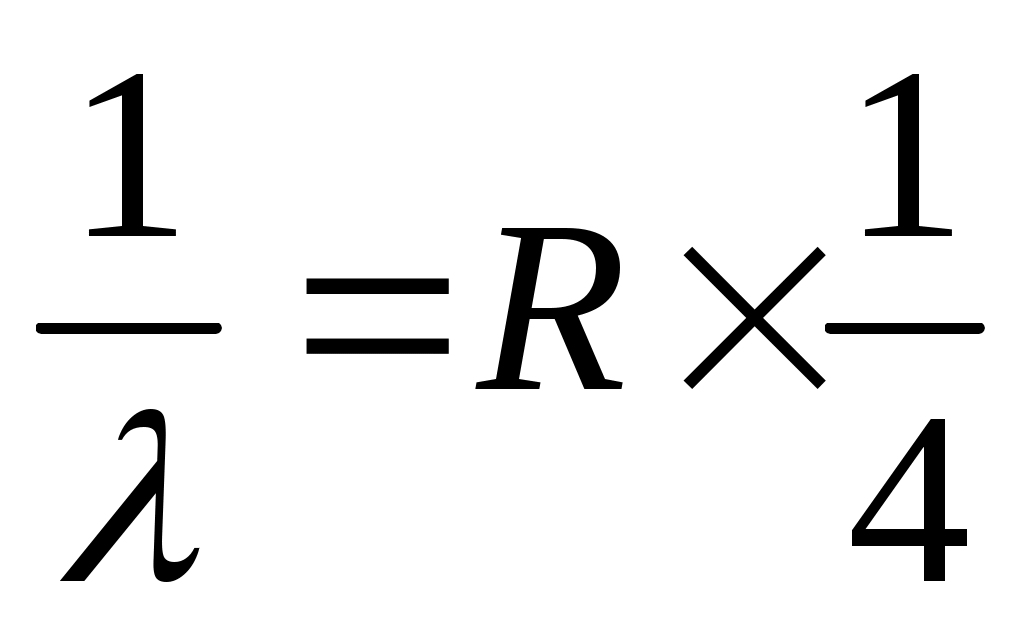
, λ1 = 1/(1,097 ∙ 107 ∙ 1/4) ∙ 109 = 364,6 (нм)
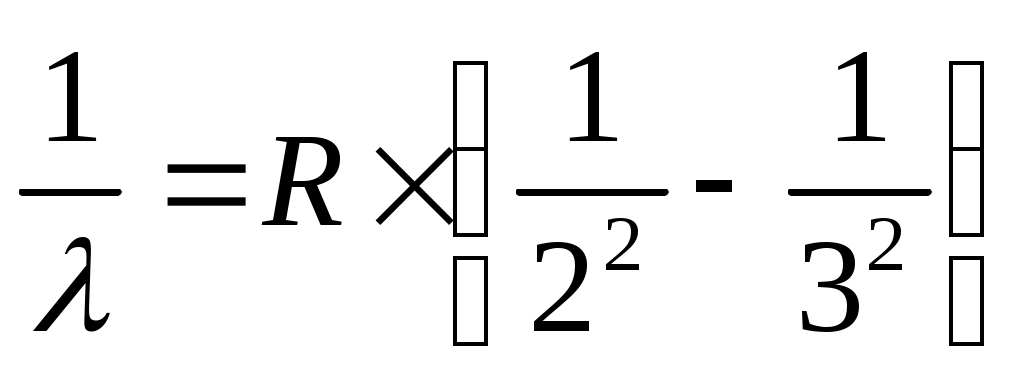
, λ∞ = 1/(1,097 ∙ 107 ∙ 0,1389) ∙ 109 = 656,3 (нм)
Для серии Пашена: m = 3, n = 4, 5 … ∞.
, R = 1,097 ∙ 107 (м-1)
при n = ∞.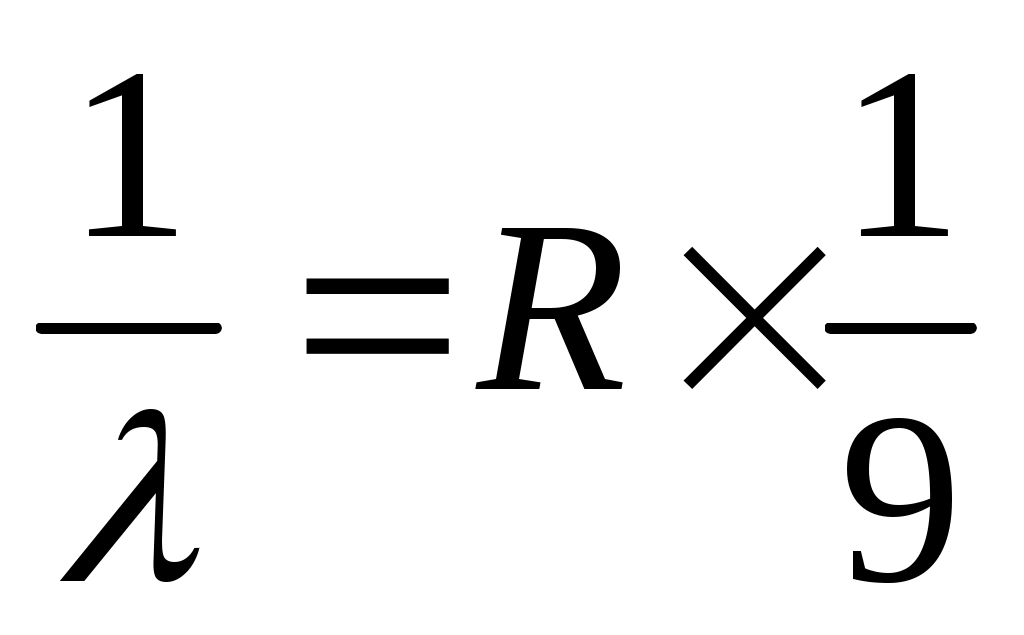
, λ1 = 1/(1,097 ∙ 107 ∙ 1/9) ∙ 109 = 820,4 (нм)
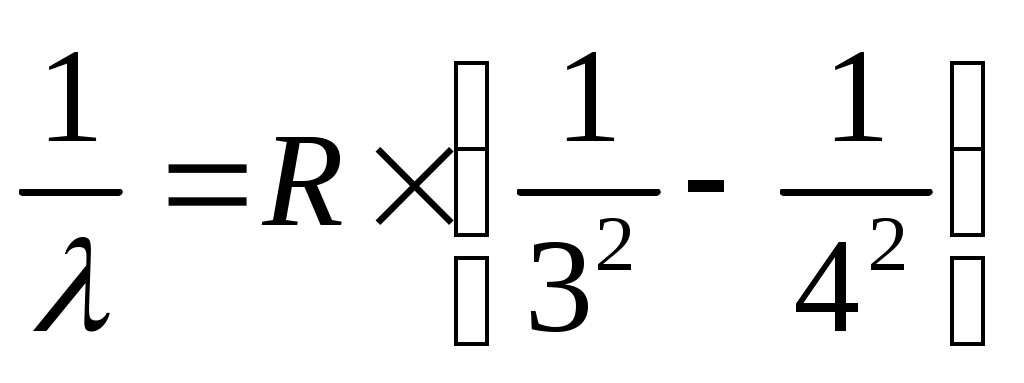, λ∞ = 1/(1,097 ∙ 107 ∙ 0,04861) ∙ 109 = 1875,3 (нм)
7. ПРИЛОЖЕНИЕ
К работе прилагается регистрационный файл (*.REG).
, умноженному на . Плотность вероятности обнаружения электрона на расстоянии r от ядра
достигает максимума при r=r0.
Величина r0, имеющая размерность длины, совпадает с радиусом первой боровской орбиты. Следовательно, в квантовой механике радиус первой боровской орбиты интерпретируется как расстояние от ядра, на котором вероятность обнаружения электрона максимальна.
-
Какому правилу отбора подчиняется орбитальное квантовое число и почему?
Из закона сохранения момента импульса при испускании и поглощении света атомом для орбитального квантового числа l возникает правило отбора
.-
Указать типы переходов для серий Лаймана и Пашена.
Для серии Лаймана: np → 1s (n = 2, 3 ...).
Для серии Пашена: np → 3s, ns → 3p, nd → 3p, np → 3d, nf → 3d (n = 4, 5 ...)
-
Найти коротковолновую и длинноволновую границы (λ1 и λ∞) для серий Лаймана, Бальмера, Пашена.
Для серии Лаймана: m = 1, n = 2, 3, … ∞.
, R = 1,097 ∙ 107 (м-1)при n = ∞.
, λ1 = 1/(1,097 ∙ 107) ∙ 109 = 91,2 (нм) , λ∞ = 1/(1,097 ∙ 107 ∙ 3/4) ∙ 109 = 121,5 (нм)Для серии Бальмера: m = 2, n = 3, 4 … ∞.
, R = 1,097 ∙ 107 (м-1)при n = ∞.
, λ1 = 1/(1,097 ∙ 107 ∙ 1/4) ∙ 109 = 364,6 (нм)
, λ∞ = 1/(1,097 ∙ 107 ∙ 0,1389) ∙ 109 = 656,3 (нм)
Для серии Пашена: m = 3, n = 4, 5 … ∞.
, R = 1,097 ∙ 107 (м-1)при n = ∞.
, λ1 = 1/(1,097 ∙ 107 ∙ 1/9) ∙ 109 = 820,4 (нм) , λ∞ = 1/(1,097 ∙ 107 ∙ 0,04861) ∙ 109 = 1875,3 (нм)7. ПРИЛОЖЕНИЕ
К работе прилагается регистрационный файл (*.REG).