1. 
   Понятие ДУ. Понятие общего решения . Понятие частного решения ДУ. Понятие особого решения ДУ.
   
2. 
   Геометрическая интерпретация обыкновенного ДУ 1-го порядка и его решения.
   
3. 
   Задача Коши для ДУ 1-го порядка. Теорема о существовании и единственности решения задачи Коши для ДУ 1-го порядка.
   
4. 
   ДУ 1-го порядка – различные виды записи.
   
5. 
   Уравнения с разделяющимися переменными и приводящиеся к ним.
   
6. 
   Однородные дифференциальные уравнения 1-го порядка и приводящиеся к ним.
   
7. 
   Линейные дифференциальные уравнения (ЛДУ) 1-го порядка. Метод Лагранжа вариации произвольной постоянной.
   
8. 
   Линейные дифференциальные уравнения (ЛДУ) 1-го порядка. Метод Бернулли.
   
9. 
   Уравнения Бернулли. Метод Бернулли.
   
10. 
    Дифференциальные уравнения высших порядков. Понижение порядка дифференциальных уравнений.
    
11. 
    Однородные линейные дифференциальные уравнения (ОЛДУ).
    
12. 
    Свойства решений ОЛДУ. Линейная зависимость и независимость функций.
    
13. 
    .Определитель Вронского и случаи решения однородных линейных дифференциальных уравнений (ОЛДУ). Формула Лиувилля.
    
14. 
    Фундаментальные системы решений (ФСР) ОЛДУ.
    
15. 
    Интегрирование ОЛДУ с постоянными коэффициентами.
    
16. 
    .Характеристическое уравнение. Случай простых корней.
    
17. 
    Характеристический многочлен. Случай кратных корней.
    
18. 
    Неоднородные линейные дифференциальные уравнения (НЛДУ). Общее решение.
    
19. 
    Метод вариации произвольных постоянных для решения НЛДУ.
    
20. 
    Интегрирование НЛДУ с постоянными коэффициентами и специальной правой частью методом подбора частных решений.
    
21. 
    Определение функции двух (трёх) переменных. Способы задания функции двух (трёх) переменных.
    
22. 
    Понятие предела функции двух переменных. Непрерывность функции нескольких переменных.
    
23. 
    Определение частной производной функции .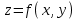
    
24. 
     Геометрический смысл частных производных функции .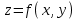
    
25. 
    Полный дифференциал функции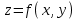 . Дифференцириуемость функции двух (трёх) переменных.
    
26. 
     Формулы вычисления производных сложных функций.
    
27. 
    Частные производные второго порядка функции .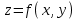
    
28. 
    Скалярное поле. Поверхности уровня. Плоское скалярное поле. Линии уровня.
    
29. 
    Понятия максимума и минимума функции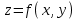 . Необходимые условия существования экстремума функции .
    
30. 
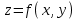    Стационарные и критические точки функции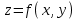 . Экстремум функции двух переменных. Достаточные условия экстремума функции .
    
31. 
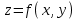    Производная функции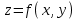 по направлению l.
    
32. 
    Определение градиента функции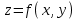 . Связь градиента с производной по направлению.
    
33. 
    Поверхности 2-го порядка.
    
34. 
    Уравнение касательной плоскости и касательной прямой к поверхности.
    
35. 
     Определение двойного интеграла.
    
36. 
    Геометрический смысл двойного интеграла.
    
37. 
     Основные свойства двойного интеграла
    
38. 
     Определение области на плоскости, правильной в направлении оси Ох.
    
39. 
    Определение области на плоскости, правильной в направлении оси Оу.
    
40. 
    Вычисление двойного интеграла в декартовых координатах.
    

---

---

Смотрите также файлы

• Такое экономика и чем занимаются экономисты. Дело в том, что в коварном русском языке у слова экономика.docx

• Тест Умеете ли Вы выступать Отвечать на вопросы нужно да или нет.docx

• План урока по музыке 6 Раздел 2А Ценности Класс 4.doc

• Мебельная фабрика может производить в месяц либо 100 письменных столов, либо 500 стульев. Какова альтернативная стоимость одного стола.docx

• Студент гр. Эжд.docx