Контрольная работа №1. Дискретная случайная величина.Вариант №5.

1. 
   
   Четыре яблока случайным образом разложили по трем корзинам. Найти вероятность того, что первая корзина осталась пустой.
   

Решение:Рассмотрим возможные варианты разложения 4-х яблок по 3-м корзинам.

4	0	0	Всего получилось n=12 вариантов, из них m=5 отвечают условию пустой 1-ой корзины. Вероятность равна:
0	4	0
0	0	4
3	1	0
1	3	0
3	0	1
1	0	3
0	1	3
0	3	1
2	2	0
2	0	2
0	2	2

2. 
   
   Найти вероятность того, что из 1461 человека ровно 1 родился 29 февраля.
   

Решение: Используем формулу Бернулли 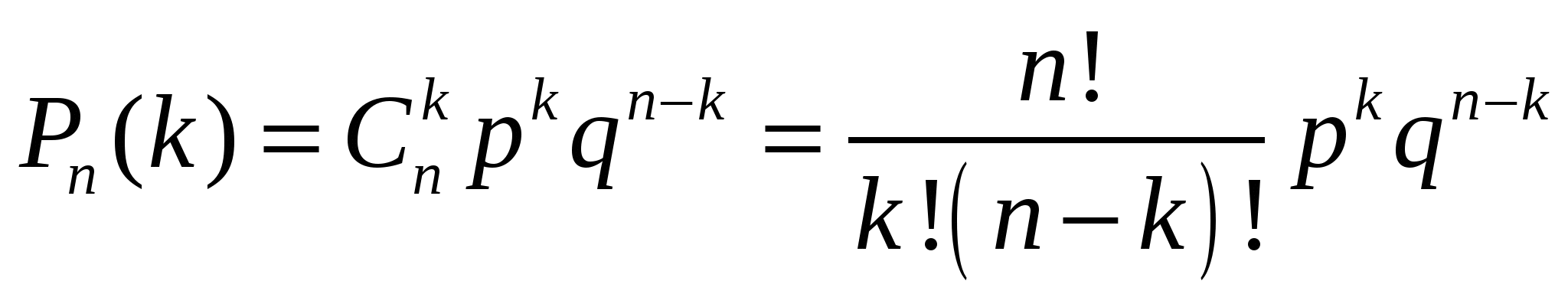  - вероятность того, что в n испытаниях событие произойдет k раз. Здесь   - вероятность родиться 29 февраля;  - вероятность не родится 29 февраля (вероятность противоположного события)Вероятность того, что из 1461 человека ровно 1 родился 29 февраля равна

---

gif" name="object5" align=absmiddle width=593 height=48>

3. 
   
   В первой урне 5 черных 3 белых шара. Во второй 2 белых, 1 черный шар. Из случайной урны берут два шара. Найти вероятность, что они белые.
   

Решение:

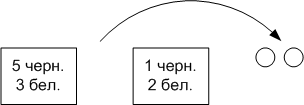Событие В1 – шары взяты из 1-ой урны; событие В2 – шары взяты из 2-ой урны; событие А- вынуты два белых шара.

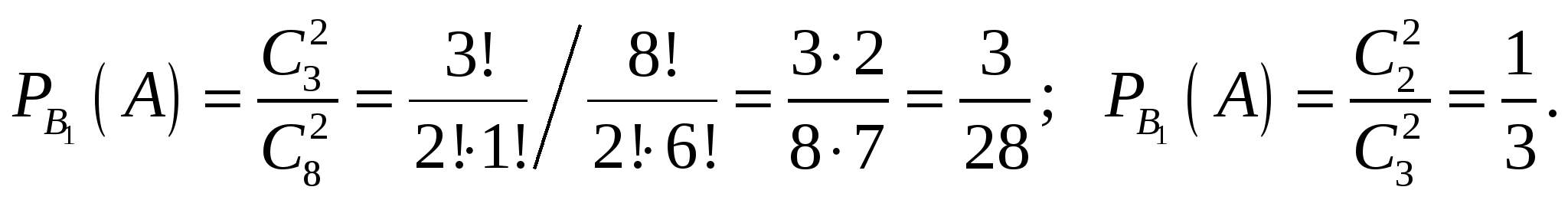
Используем формулу полной вероятности событий. . Условные вероятности   и   рассчитываются по формулам:Подставим найденные вероятности в формулу полной вероятности, получим

4. 
   
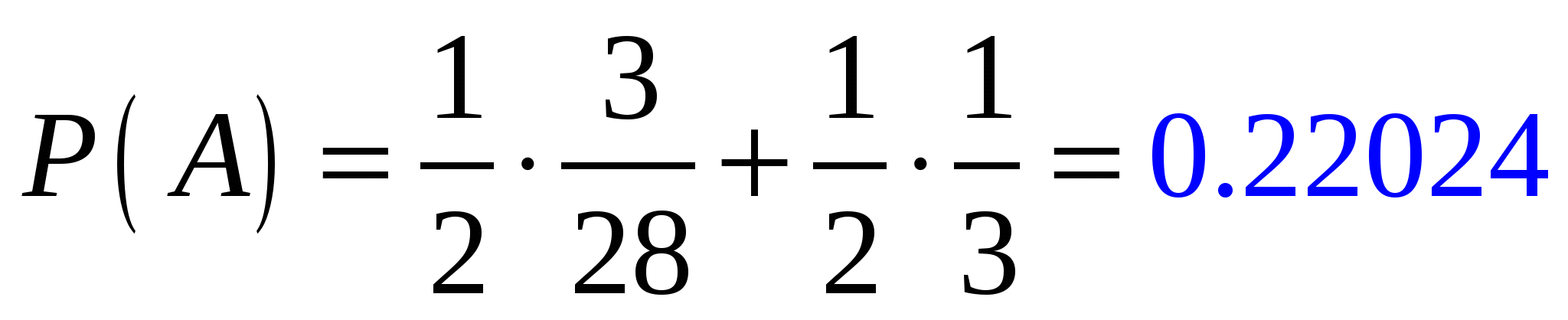
   В колоде 36 карт. Берут 2 карты. Случайная величина Х - число тузов среди взятых карт.. Найти закон распределения Х, математическое ожидание, дисперсию
   

Решение: Составим закон распределения случайной величины Х. 

X	0	1	2
P	Р1	Р2	Р3

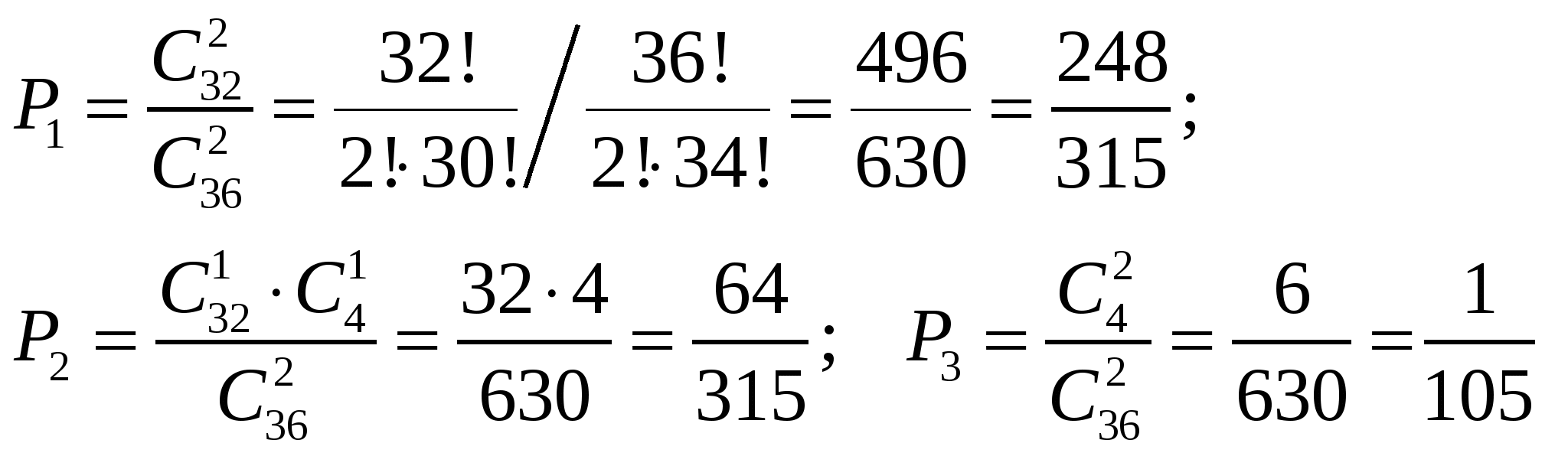
ЗдесьСделаем проверку  .Закон распределения имеет вид:

X	0	1	2
P

---

Найдем математическое ожиданиеНайдем дисперсию Контрольная работа №1. Дискретная случайная величина.Вариант №14.

1. 
   
   Найти вероятность того, что при случайной раздаче 52 карт четырем игрокам, все пики окажутся у первого игрока.
   

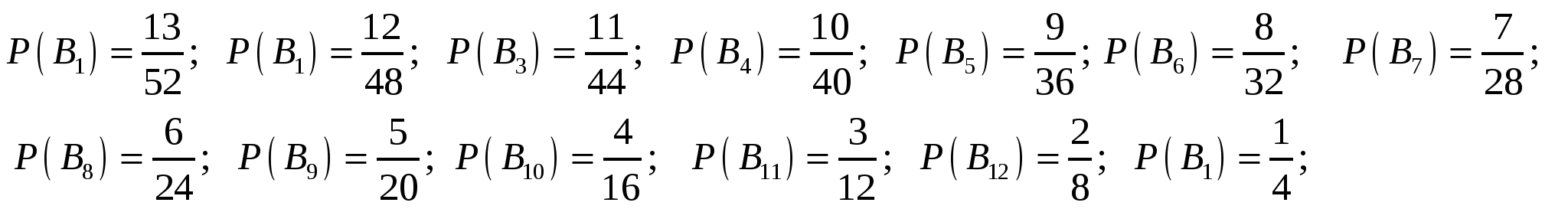
Решение:В колоде 52/4=13 карт масти пик, событие   - выпадение пики 1-му игроку на i-ом круге раздачи  , событие А – у первого игрока оказались 13 карт масти пик.. Вероятности событий   равныВероятность события А равна произведению вероятностей этих событий

2. 
   
   Найти вероятность того, что из 365 человек мене двух родились первого января.
   

Решение:Вероятность родится одному человеку 1-го января равна  , вероятность родится в любой другой день равна Вероятность того, что из 365 человек мене двух родились первого января равнасумме вероятностей того, что ни один человек из 365 не родился в этот день и один из них родился в этот день  . Данные вероятности рассчитываем по формуле Бернулли 

---

3. 
   
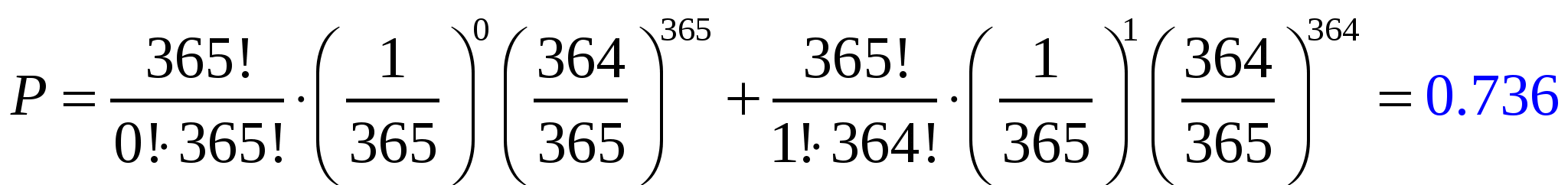
   В первой колоде 36 карт. Во второй колоде 52 карты. Из первой колоды во вторую кладут 2 карты. Из второй потом берут карту. Найти вероятность того, что взятая карта туз. 
   

Событие В1 – переложили из 1-ой колоды во 2-ю - 2-а туза; событие В2 – переложили из 1-ой колоды во 2-ю - 1туза и 1 не туз;  событие В3 – переложили из 1-ой колоды во 2-ю - 2 не туза;  событие А- вынуты из 2-ой колоды один туз.

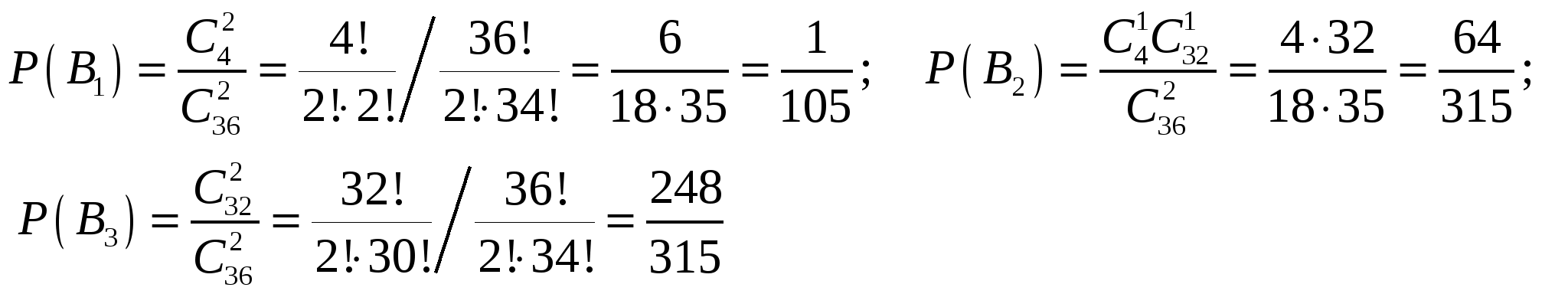
Запишем вероятность события А, используя формулу полной вероятности.Здесь вероятности событий   равныНайдем условные вероятности. Подставим все вероятности в формулу полной вероятности, получим

4. 
   
   У стрелка 4 патрона. Вероятность попадания по мишени при одном выстреле равна 0.6. Стрельба ведется до первого попадания. Случайная величина Х - число оставшихся не израсходованных патронов. Найти закон распределения Х, математическое ожидание, дисперсию.
   

Решение: Составим закон распределения случайной величины Х. 

X	0	1	2	3
P	Р1	Р2	Р3	Р4

Здесь р₄ =0,6 – вероятность попадания с первого выстрела (осталось 3 патрона);р₃ =0,6·0,4=0,24 – вероятность попадания со 2-го выстрела (осталось 2 патрона);р₂ =0,6·0,4²=0,096 – вероятность попадания с 3-го выстрела (остался 1 патрона);р₁

---

 =0,6·0,4³+0,4⁴=0,064 – вероятность попадания с 4-го выстрела плюс вероятность четырехкратного промаха (патронов не осталось);

Проверка: 0,6+0,24+0,096+0,064=1

Закон распределения имеет вид:

X	0	1	2	3
P	0,064	0,096	0,24	0,6

Найдем математическое ожиданиеНайдем дисперсию 

---

Смотрите также файлы

• Законом О статусе депутата Государственной Думы и члена Совета Федерации Федерального Собрания Российской Федерации.docx

• Отчет по лабораторной работе по дисциплине Методология и технологии проектирования информационных систем.docx

• Учебное пособие организационноправовые основы местного самоуправления в российской федерации.pdf

• Понятие, структура и виды административноправовых норм.docx

• Жиынты баалауа арналан дістемелік нсаулытар Биология.docx