Файл: Лабораторная работа 3 Программирование циклических алгоритмов.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 01.12.2023

Просмотров: 27

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

ЛАБОРАТОРНАЯ РАБОТА №3




Программирование циклических алгоритмов




Согласно варианту, написать программу на языке программирования Pascal и составить блок-схему алгоритма:

Каждую задачу (часть 1 и 2) решить, используя три цикла.

Часть 1


  1. Найти все двузначные числа, сумма цифр которых не меняется при умножении числа на 2,3,4,5,6,7,8,9.

  2. Найти все трехзначные числа, сумма цифр которых равна данному целому числу.

  3. Найти все трехзначные числа, средняя цифра которых равна сумме первой и третьей цифр.

  4. Найти все трехзначные числа, которые можно представить разностью между квадратом числа, образованного первыми двумя цифрами и квадратом третьей цифры.

  5. Найти все двузначные числа, сумма квадратов цифр которых делится на 17.

  6. Найти все трехзначные числа, представимые в виде сумм факториалов своих цифр.

  7. Найти двузначное число, обладающее тем свойством, что куб суммы его цифр равен квадрату самого числа.

  8. Найти двузначное число, равное утроенному произведению его цифр.


  9. В каких двузначных числах удвоенная сумма цифр равна их произведению?

  10. Можно ли заданное натуральное число М представить в виде суммы квадратов двух натуральных чисел? Написать программу решения этой задачи.

  11. Билет называют «счастливым», если в его номере сумма первых трех цифр равна сумме последних трех. Организовать ввод номера билета и определить, является ли он счастливым.

  12. Запишите любое число от 1 до 1000, введенное пользователем, русскими буквами. Например, 2 – два, 150 – сто пятьдесят.

  13. Дано четырехзначное число N. Выяснить:

       a. Является ли число палиндромом?

  14. Трамвайный билет имеет шестизначный номер. Выяснить, является ли билет "счастливым". Билет назовем "счастливым", если сумма первых трех цифр равна сумме последних трех цифр. Примечание. Так как шестизначное число больше 32767 (тип Integer), необходимо номер билета определит как тип Longint(до 10 знаков).

  15.  Дано натуральное число N. Определить, является ли оно простым, т.е. делится нацело только на 1 и на само себя

  16.  Даны натуральные числа M и N. Определить, являются ли они взаимно простыми. Взаимно простые числа не имеют общих делителей, кроме 1.

  17. Дано натуральное число N. Определить все простые числа не превосходящие N.

  18. Дано натуральное число N. Определить, является ли оно совершенным. Совершенное число N равно сумме всех своих делителей, не превосходящих само N.

Часть 2
Вычисление выражений:

Дано натуральное n. Вычислить:

  1. ;

  2. ;
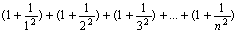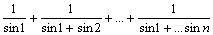    Дано действительное число х, натуральное число n. Вычислить:

  3. x ( x - n )( x - 2 n )( x - 3 n )…( x - n2 );

  4.  ;
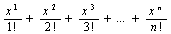    Дано натуральное n. Вычиcлить:

  5.  ;

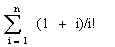Вычислить приближенно значение бесконечной суммы (справа от каждой суммы дается ее точное значение, с которым можно сравнить полученный ответ):

  1. =  ;

  2. =  ;
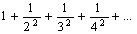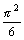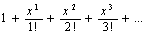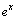    Нужное приближение считается полученным, если вычислена сумма нескольких первых слагаемых, и очередное слагаемое оказалось по модулю меньше данного положительного числа e.

  3. Даны два целых числа A и B (A < B). Вывести все целые числа, расположенные между данными числами (не включая сами эти числа), в порядке их возрастания, а также количество N этих чисел.

  4. Даны два целых числа A и B (A < B). Вывести все целые числа, расположенные между данными числами (включая сами эти числа), в порядке их убывания, а также количество N этих чисел.

  5. Дано вещественное число A и целое число N (> 0). Вывести A в степени N: AN = A·A·...·A (числа A перемножаются N раз).

  6. Дано вещественное число A и целое число N (> 0). Вывести все целые степени числа A от 1 до N.

  7. Дано вещественное число A и целое число N (> 0). Вывести 1 + A + A2 + A3 + ... + AN.

  8. Дано вещественное число A и целое число N (> 0). Вывести 1 - A + A2 - A3 + ... + (-1)NAN.

  9. Дано целое число N (> 1). Вывести наименьшее целое K, при котором выполняется неравенство 3K > N, и само значение 3K.

  10. Дано целое число N (> 1). Вывести наибольшее целое K, при котором выполняется неравенство 3K < N, и само значение 3K.

  11. Дано вещественное число A (> 1). Вывести наименьшее из целых чисел N, для которых сумма 1 + 1/2 + ... + 1/N будет больше A, и саму эту сумму.

  12. Дано вещественное число A (> 1). Вывести наибольшее из целых чисел N, для которых сумма 1 + 1/2 + ... + 1/N будет меньше A, и саму эту сумму.

  13. Дано целое число N (> 0). Вывести произведение 1·2·...·N. Чтобы избежать целочисленного переполнения, вычислять это произведение с помощью вещественной переменной и выводить его как вещественное число.

  14. Дано целое число N (> 0). Если N - нечетное, то вывести произведение 1·3·...·N; если N - четное, то вывести произведение 2·4·...·N. Чтобы избежать целочисленного переполнения, вычислять это произведение с помощью вещественной переменной и выводить его как вещественное число.

  15. Дано целое число N (> 2) и две вещественные точки на числовой оси: A, B (A < B). Отрезок [A, B] разбит на равные отрезки длины H с концами в N точках вида A, A + H, A + 2H, A + 3H, ..., B. Вывести значение H и набор из N точек, образующий разбиение отрезка [A, B].

  16. Дано целое число N (> 2) и две вещественные точки на числовой оси: A, B (A < B). Функция F(X) задана формулой F(X) = 1 - sin(X). Вывести значения функции F в N равноотстоящих точках, образующих разбиение отрезка [A, B]: F(A), F(A + H), F(A + 2H), ..., F(B).

  17. Дано число D (> 0). Последовательность чисел AN определяется следующим образом: A1 = 2, AN = 2 + 1/AN-1, N = 2, 3, ... Найти первый из номеров K, для которых выполняется условие |AK - AK-1| < D, и вывести этот номер, а также числа AK-1 и AK.

  18. Дано число D (> 0). Последовательность чисел AN определяется следующим образом: A1 = 1, A2 = 2, AN = (AN-2+ AN-1)/2, N = 3, 4, ... Найти первый из номеров K, для которых выполняется условие |AK AK-1| < D, и вывести этот номер, а также числа AK-1 и AK.


Контрольные вопросы



  1. Как записывается и как работает оператор FOR?


  2. Для организации каких циклов применим оператор FOR?


  3. В чем отличие оператора WHILE от оператора REPEAT?


  4. Как программируются циклические алгоритмы с явно заданным числом повторений цикла?


  5. Как программируются циклические алгоритмы с заранее неизвестным числом повторений цикла?

  6. Напишите оператор цикла, который не выполняется ни разу.

  7. Напишите оператор цикла, который выполняется неограниченное число раз.

  8. Замените оператор "Repeat A Until B" равносильным фрагментом программы с оператором While.



Смотрите также файлы