Файл: Лабораторная работа 5 Обработка экспериментальных данных Вариант 3 (подпись).docx

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)Кафедра информационных управляющих системЛабораторная работа № 5«Обработка экспериментальных данных»Вариант 3(подпись)Проверил ___________________________ В.Л. Литвинов(оценка и подпись)

Содержание:

Цель:

В результате эксперимента была определена некоторая табличная зависимость. С помощью метода наименьших квадратов определить линию регрессии, рассчитать коэффициент корреляции, подобрать функциональную зависимость заданного вида, вычислить коэффициент регрессии. Определить суммарную ошибку. Найти приближенное значение функции при заданном значении аргумента с помощью сплайн-интерполяции. Функция задана таблично.

Задание на лабораторную работу:

5.1В результате эксперимента была определена некоторая табличная зависимость. С помощью метода наименьших квадратов определить линию регрессии, рассчитать коэффициент корреляции, подобрать функциональную зависимость заданного вида, вычислить коэффициент регрессии. Определить суммарную ошибку.5.2Найти приближенное значение функции при заданном значении аргумента с помощью функции линейной интерполяции. Функция задана таблично.

---

Теоретическая часть:

Метод наименьших квадратов позволяет по экспериментальным данным подобрать такую аналитическую функцию, которая проходит настолько близко к экспериментальным точкам, насколько это возможно. Пусть в результате эксперимента были получены некоторые данные, отображенные в виде таблицы Требуется построить аналитическую зависимость, наиболее точно описывающую результаты эксперимента. Идея метода наименьших квадратов заключается в том, что функцию Y = f(x, a0, a1, . . . , ak) необходимо подобрать таким образом, чтобы сумма квадратов отклонений измеренных значений yi от расчетных Yi была наименьшей. функций является прямая, описываемая уравнением вида y = a1 + a2x, которая называется линией регрессии y на x. Параметры a1 и a2 являются коэффициентами регрессии. Показатель, характеризующий тесноту линейной связи между x и y, называемый коэффициентом корреляции.

Методика исследования:

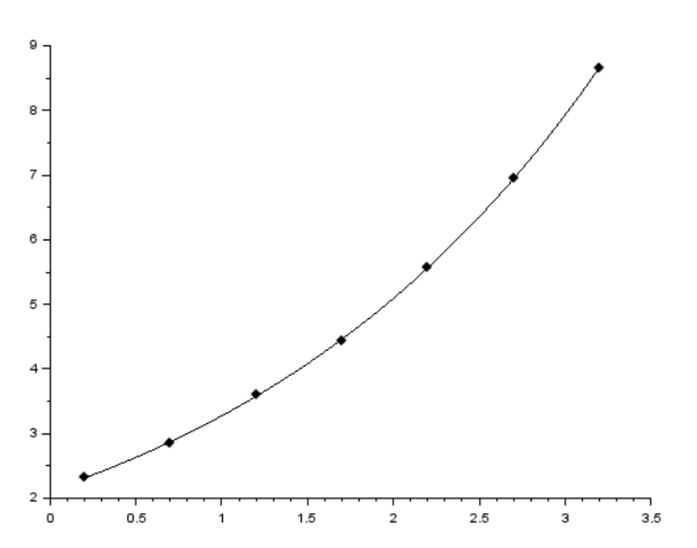
5.1Задали функцию с исходными значениями, далее нашли коэффициенты функциональной зависимости, посчитали суммарную ошибку.Определили коэффициент корреляции:Посторили исходные точки:Задали точки для графика функциональной зависимости:Построили график функциональной зависимости:График функции зависимости:Нашли коэффициенты регрессии и построили линию регрессии:

---

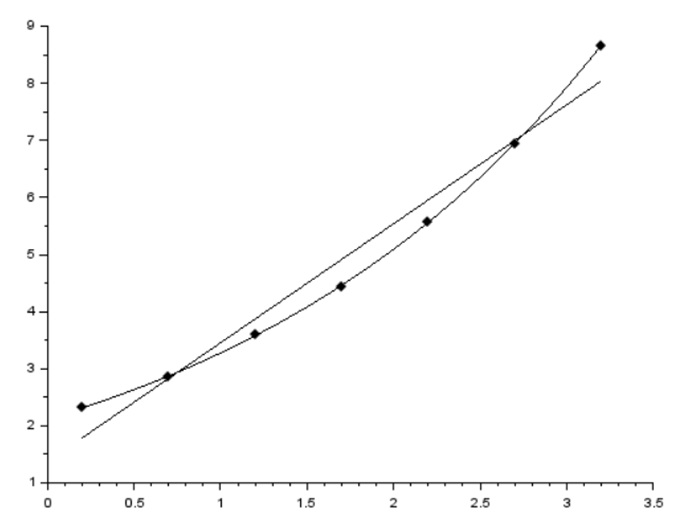
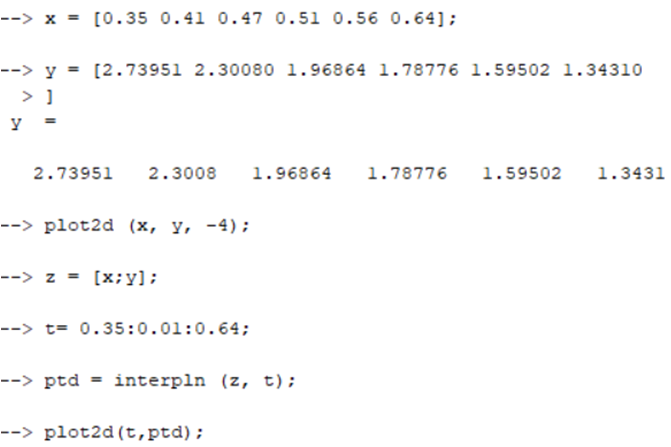
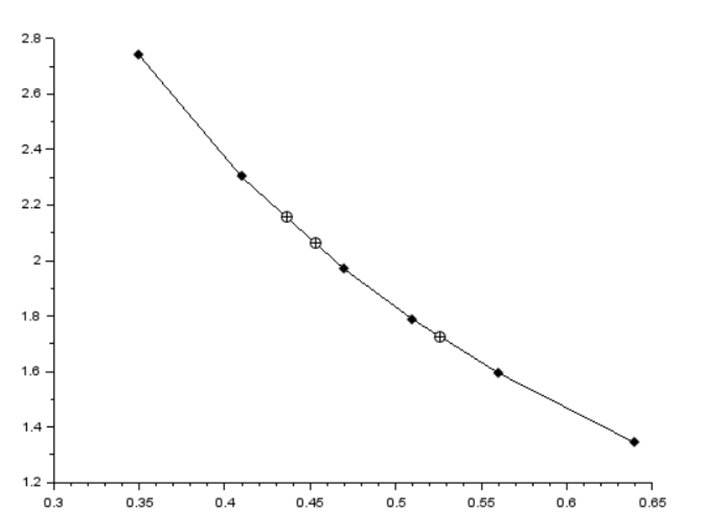
5.2Определим начальные параметры, построим заданные точки и график:Зададим исходные точки, вычислим их значение функции и нанесем на график:Где значения Y - искомые значения функции(приблеженные) в заданных точках.Получившийся график функции:Искомые точки помечены знаком "+" в окружности.

Вывод:

В результате выполнения лабораторной работы были изучены методы обработки экспериментальных данных и применение функций интерполяции в программной среде Scilab.

---