Файл: Урок 12. Глава Отношения, пропорции, проценты (26 часов) Тема. Прямая и обратная пропорциональность. Ср 3.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.12.2023
Просмотров: 29
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
кг Прямая пропорциональность
4 т – х кг
Решение.
Т.к. величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
1) 4 т = 4000 кг;
2)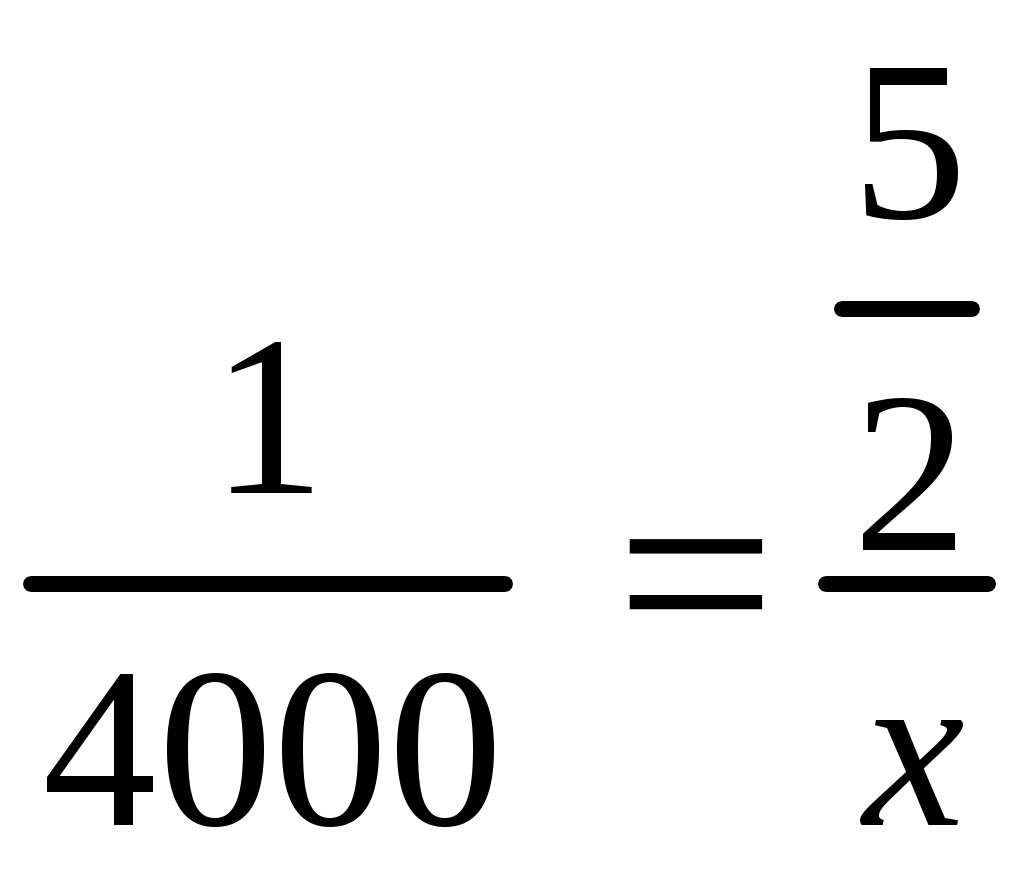 ,
,
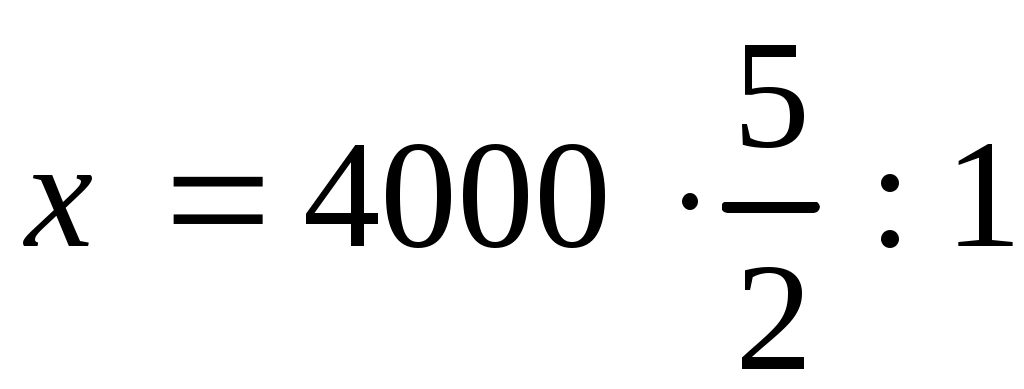 ,
,
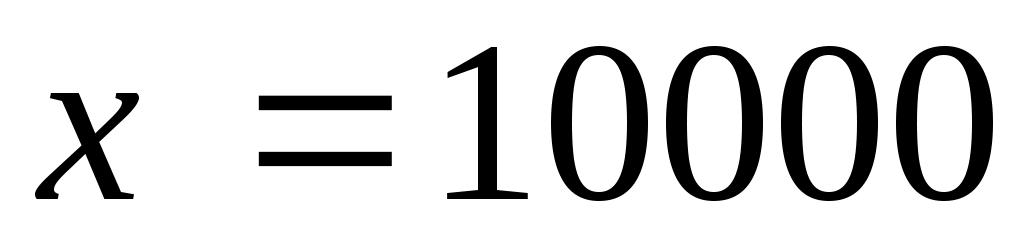 .
.
10 000 кг руды заменяют 4 т металлолома. Ответ: 10 000 кг.
Уч.с.22 № 84(а). Автомобилист заметил, что со скоростью 60 км/ч он проехал мост через реку за 40 с. На обратном пути он проехал этот же мост за 30 с. Определите скорость автомобиля на обратном пути?
 v t
v t
6 0 км/ч – 40 с Обратная пропорциональность
0 км/ч – 40 с Обратная пропорциональность
х км/ч – 30 с
Решение.
Т.к. величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
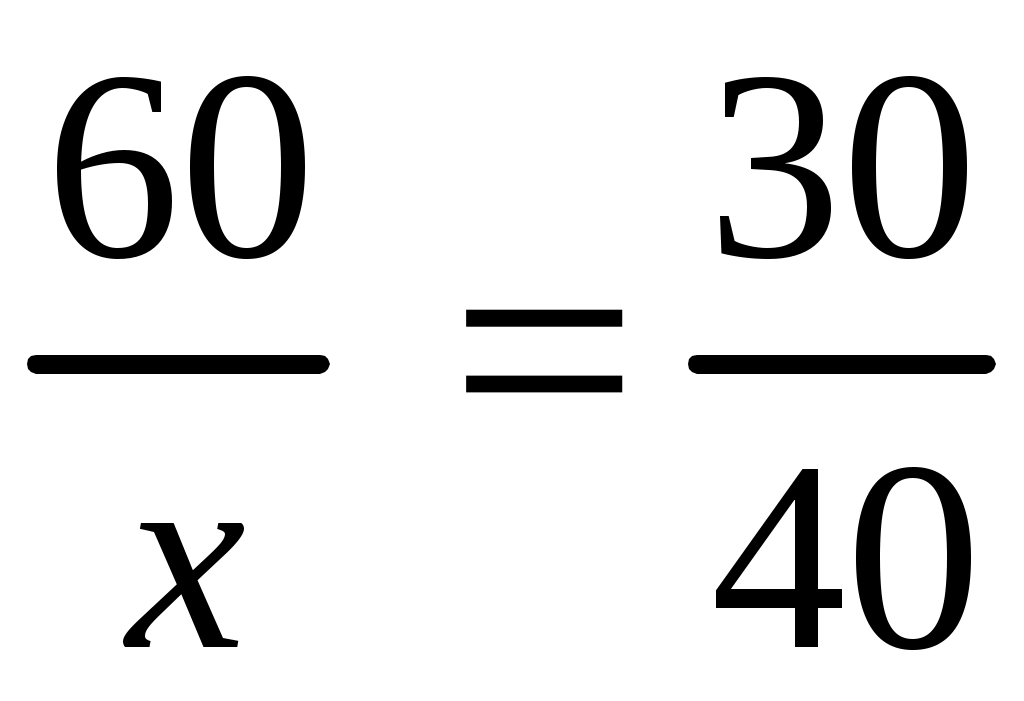 ,
,
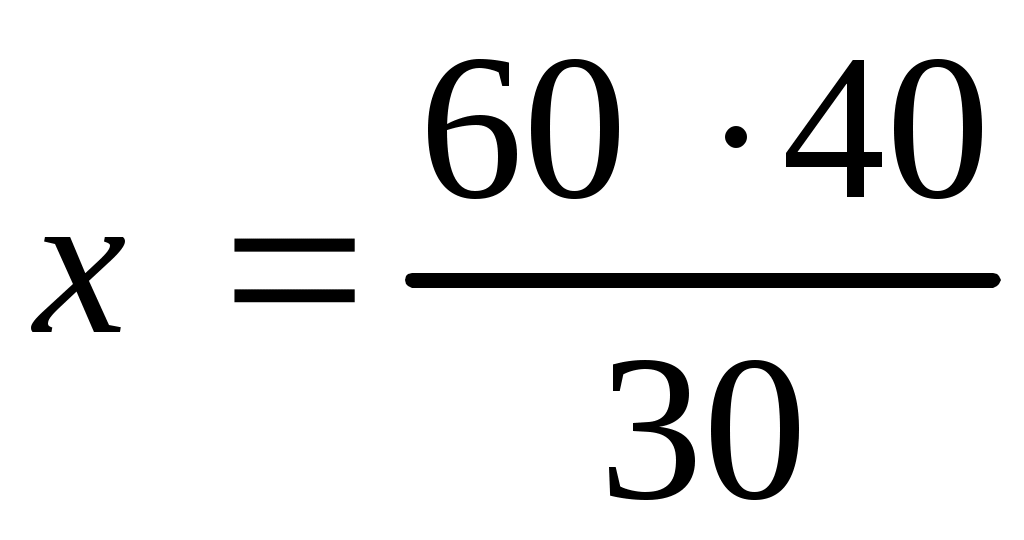 ,
,
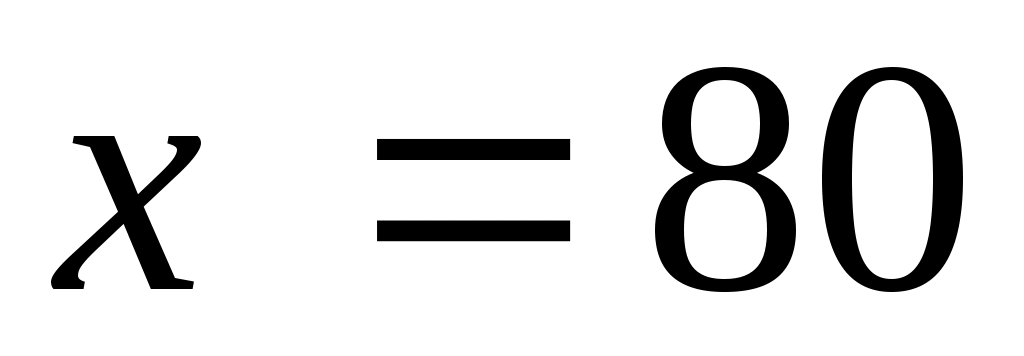 .
.
80 км/ч скорость автомобиля на обратном пути. Ответ: 80 км/ч.
4 т – х кг
Решение.
Т.к. величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
1) 4 т = 4000 кг;
2)
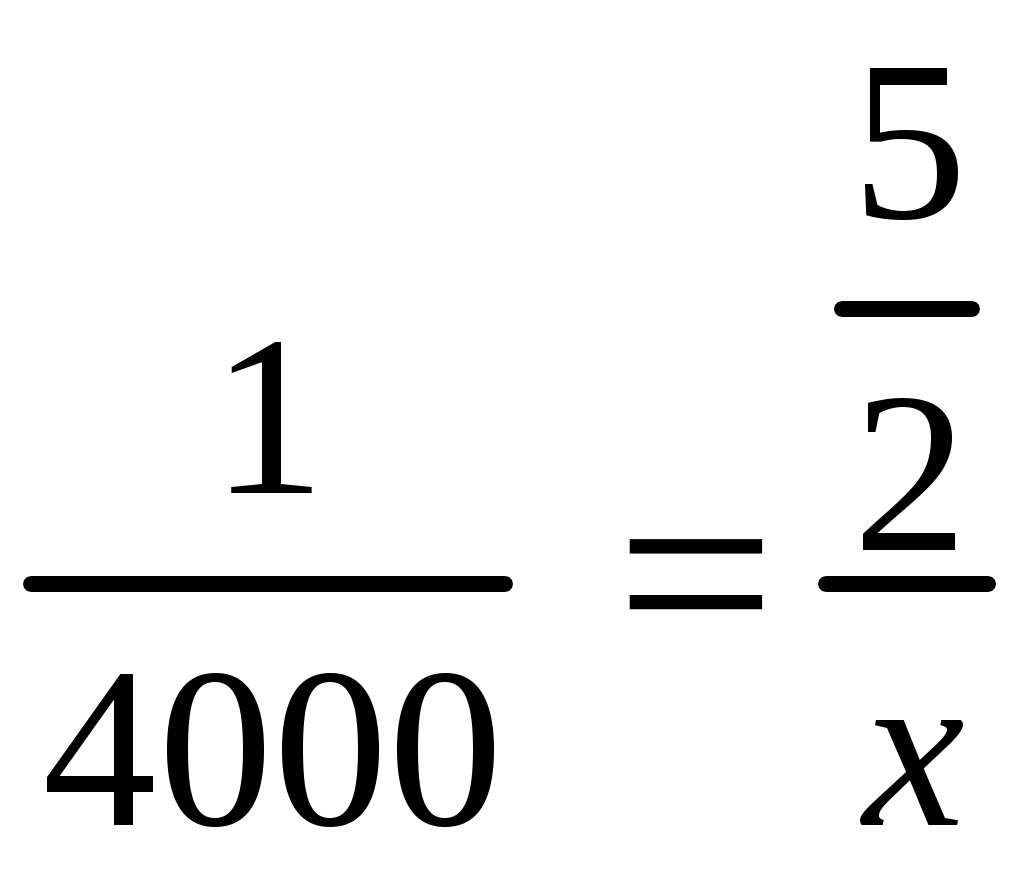 ,
,10 000 кг руды заменяют 4 т металлолома. Ответ: 10 000 кг.
Уч.с.22 № 84(а). Автомобилист заметил, что со скоростью 60 км/ч он проехал мост через реку за 40 с. На обратном пути он проехал этот же мост за 30 с. Определите скорость автомобиля на обратном пути?
 v t
v t6
 0 км/ч – 40 с Обратная пропорциональность
0 км/ч – 40 с Обратная пропорциональностьх км/ч – 30 с
Решение.
Т.к. величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
80 км/ч скорость автомобиля на обратном пути. Ответ: 80 км/ч.
-
Подведение итогов урока -
Домашнее задание. § 1.5 (выучить теорию). № 73, 75(б), 77(а), 84(б).
| Алгоритм решения задач. 1. Составить краткую запись и определить вид пропорциональности. (Одноименные величины записываются друг под другом) 2. Составить пропорцию. Если две величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины. Если две величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины. 3. Найти неизвестный член пропорции. 4. Проанализировать полученный результат и записать ответ. | Алгоритм решения задач. 1. Составить краткую запись и определить вид пропорциональности. (Одноименные величины записываются друг под другом) 2. Составить пропорцию. Если две величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины. Если две величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины. 3. Найти неизвестный член пропорции. 4. Проанализировать полученный результат и записать ответ. |
| Алгоритм решения задач. 1. Составить краткую запись и определить вид пропорциональности. (Одноименные величины записываются друг под другом) 2. Составить пропорцию. Если две величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины. Если две величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины. 3. Найти неизвестный член пропорции. 4. Проанализировать полученный результат и записать ответ. | Алгоритм решения задач. 1. Составить краткую запись и определить вид пропорциональности. (Одноименные величины записываются друг под другом) 2. Составить пропорцию. Если две величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины. Если две величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины. 3. Найти неизвестный член пропорции. 4. Проанализировать полученный результат и записать ответ. |
| Алгоритм решения задач. 1. Составить краткую запись и определить вид пропорциональности. (Одноименные величины записываются друг под другом) 2. Составить пропорцию. Если две величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины. Если две величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины. 3. Найти неизвестный член пропорции. 4. Проанализировать полученный результат и записать ответ. | Алгоритм решения задач. 1. Составить краткую запись и определить вид пропорциональности. (Одноименные величины записываются друг под другом) 2. Составить пропорцию. Если две величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины. Если две величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины. 3. Найти неизвестный член пропорции. 4. Проанализировать полученный результат и записать ответ. |
| Алгоритм решения задач. 1. Составить краткую запись и определить вид пропорциональности. (Одноименные величины записываются друг под другом) 2. Составить пропорцию. Если две величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины. Если две величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины. 3. Найти неизвестный член пропорции. 4. Проанализировать полученный результат и записать ответ. | Алгоритм решения задач. 1. Составить краткую запись и определить вид пропорциональности. (Одноименные величины записываются друг под другом) 2. Составить пропорцию. Если две величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины. Если две величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины. 3. Найти неизвестный член пропорции. 4. Проанализировать полученный результат и записать ответ. |