Добавлен: 01.12.2023
Просмотров: 94
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ (ВолгГТУ)
Факультет автомобильного транспорта
Кафедра «Техническая эксплуатация и ремонт автомобилей»
Семестровая работа по дисциплине
«Основы научных исследований»
Тема: «Момент инерции»
Выполнил:
студент группы АТ-313
Самохвалова А.А.
«01» декабря 2021 г.___________
(подпись)
Проверил:
кандидат технических наук,
доцент, Федин А.П.
Волгоград,2021
Содержание
Введение………………………………………………………………….………..3
1. Осевой момент инерции……………………………………………………….4
1.1. Теорема Гюйгенса-Штейнера………………………………………...4
1.2. Осевые моменты инерции некоторых тел……………………………5
1.3. Безразмерные моменты инерции планет и их спутников…………...7
2. Центробежный момент инерции момент инерции……..…………………….8
3. Геометрический момент инерции……………………………………………..9
4. Центральный момент инерции……………………………………….............10
5. Тензор инерции и эллипсоид инерции…………...………………………….11
6. Пример решения задач на нахождение момента инерции…………………13
Заключение………………………………………………………………….……14
Список использованной литературы………………………………………...…16
Введение
Понятие «инерция» в физике рассматривается, как способность тел какое-то время сохранять состояние движения при отсутствии действия внешних сил. Данное понятие также пользуется достаточно частым применением как в области естествознания, так и в нашей обыденной жизни. Зачастую «инертным» считают того человека, который вообще не проявляет никакой инициативы, выполняет лишь то, что ему велят другие, и причем очень медленно, совершенно без энтузиазма. «Движется по инерции», – говорят все, подчеркивая, что-то, что делается без какого-либо смысла, а просто потому, что так было принято когда-то или потому, что стало давней привычкой. Понятие инерции довольно простое, но для объяснения «момента инерции» потребуется больше пояснений.
Масса – мера инертности тела. Если скатить несколько бочек с разной массы, то остановить сложнее будет именно ту, которая тяжелее. Из этого следует вывод, что чем больше масса, тем большее внешнее воздействие необходимо, для того, чтобы изменить движение тела. Это относится к поступательному движению, когда тележка из примера движется по прямой. Точно также с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси .
Момент инерции - это скалярная физическая величина, мера инерции тела при вращении вокруг оси, характеризующаяся распределением масс в теле: момент инерции = сумме произведений элементарных масс на квадрат их расстояния до базового набора (точка, линия или плоскость).
Единицей измерения СИ является: кг·м².
Обозначение: I или J
С учетом многообразия, от которого отсчитывается расстояние точек, существует всего несколько видов моментов инерции.
1. Осевой момент инерции
1.1. Теорема Гюйгенса-Штейнера
Момент инерции твердого тела относительно любой оси зависит как от формы, массы и размера тела, так и от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера) момент инерции тела J относительно произвольной оси равен сумме моментов инерции этого тела Jc относительно оси, проходящей через центр масс тела. тело, параллельное рассматриваемой оси, и произведение массы тела m на квадрат расстояния d между осями:
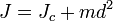
Если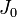 
это момент инерции тела относительно оси, проходящей через центр масс тела, то момент инерции относительно параллельной оси, находящейся на расстоянии d от нее, будет равен:
,
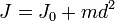где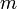 
— полная масса тела.
Момент инерции стержня относительно оси, проходящей через его конец, будет равен :
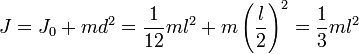
1.2. Осевые моменты инерции некоторых тел
Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения
| Тело | Описание | Положение оси a | Момент инерции Ja |
 | Материальная точка массы m | На расстоянии r от точки, неподвижная |  |
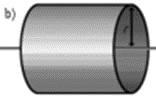 | Полый тонкостенный цилиндр или кольцо радиуса r и массы m | Ось цилиндра | |
 | Сплошной цилиндр или диск радиуса r и массы m | Ось цилиндра |  |
 | Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1 | Ось цилиндра |  |
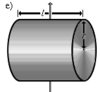 | Сплошной цилиндр длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его середину |  |
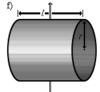 | Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его середину |  |
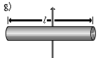 | Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его середину |  |
 | Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его конец |  |
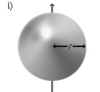 | Тонкостенная сфера радиуса r и массы m | Ось проходит через центр сферы |  |
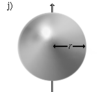 | Шар радиуса r и массы m | Ось проходит через центр шара |  |
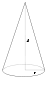 | Конус радиуса r и массы m | Ось конуса |  |
Таблица.1. Моменты инерции однородных тел
1.3. Безразмерные моменты инерции планет и их спутников
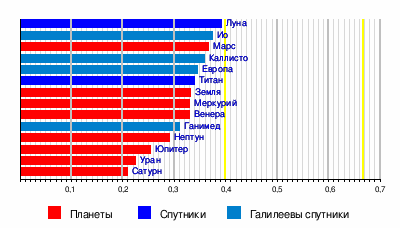
Рис.1. Безразмерные моменты инерции планет и их спутников
Безразмерные моменты инерции имеют огромный смысл для исследования внутреннего строения планет и их спутников. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки такой же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равном mr2) . Это значение отражает распределение массы по глубине.
Одним из методов его измерения на планетах и спутниках является определение доплеровского сдвига радиосигнала, передаваемого AMC, летящим вокруг данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции составляет 2/3 ( 0,67), для однородной сферы - 0,4, и, как правило, чем меньше, тем большая масса тела сосредоточена в его центре. Например, Луна имеет безразмерный момент инерции, близкий к 0,4 (равный 0,391), поэтому предполагается, что она относительно однородна, ее плотность мало меняется с глубиной. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования плотного ядра.
2. Центробежный момент инерции
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются такие величины как:
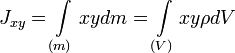
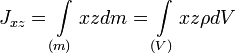
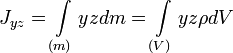
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm. Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно = 0. Через каждую точку тела можно провести три основные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трех главных осей инерции, проведенных в произвольной точке O тела, называются основными моментами инерции тела. Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей называются его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.
3. Геометрический момент инерции
Геометрический момент инерции это геометрическая характеристика сечения вида,
где z — расстояние от центральной оси y(z) до любой элементарной площадки dF относительно нейтральной оси.
Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для расчета радиуса инерции, отклонения луча.
Единица измерения СИ — м4. В строительных расчетах, литературе и сортиментах металлопроката, в частности, указывается в см4. Отсюда выражается момент сопротивления секции:
.
| Прямоугольника высотой h и шириной b: |   |
| Прямоугольного коробчатого сечения высотой и шириной по внешним контурам H и B, а по внутренним h и b соответственно |   |
| Круга радиусом r |  |
Таблица 2. Геометрические моменты инерции некоторых фигур
4. Центральный момент инерции
Центральный момент инерции
(или момент инерции относительно точки O) это величина:
,
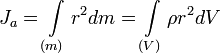
где:
-
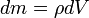— масса малого элемента объёма тела dV, -
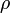— плотность, -
— расстояние от элемента dV до точки O.
Центральный момент инерции может быть выражен через основные осевые или центробежные моменты инерции:
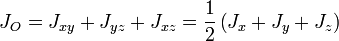.5. Тензор инерции и эллипсоид инерции
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором
, можно представить в виде квадратичной (билинейной) формы:
(1),где
— тензор инерции. Матрица тензора инерции симметрична, имеет размеры 
и состоит из компонент центробежных моментов:
, 
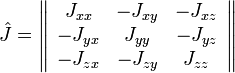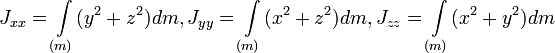
При выборе подходящей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нам нужно решить задачу на собственные значения тензорной матрицы
:
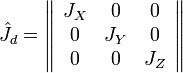
Где,
—ортогональная матрица перехода к собственному базису тензора инерции. В собственном базисе оси координат направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины
— главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
.Откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на
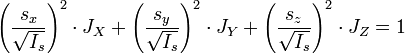
и произведя замены:
,получаем канонический вид уравнения эллипсоида в координатах
:
Расстояние от центра эллипсоида до некоторых его точек связано со значением момента инерции тела по прямой, проходящей через центр эллипсоида и эту точку :
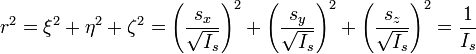
6. Пример решения задач на нахождение момента инерции
Задача 1. Найти момент инерции обруча массой и радиусом относительно оси, проходящей через его край перпендикулярно обручу.
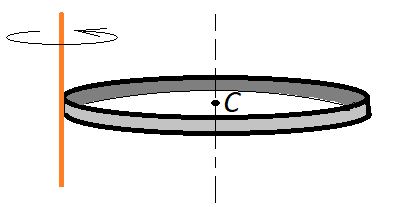
Рис. 6.1. Нахождение момента инерции обруча
Решение:
П
о таблице определим момент инерции обруча (кольца), и прибавим произведение массы тела на квадрат расстояния между осями, а это – радиус кольца. ТогдаОтвет:
.Заключение
Данная работа посвящена изучению понятия инерции и определения момента инерции. Момент инерции тонкого кольца (ось вращения перпендикулярна плоскости кольца и проходит через центр):