Файл: 11 сынып Алгебра жне анализ бастамалары пнінен байау емтихан тапсырмалары.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.12.2023
Просмотров: 197
Скачиваний: 48
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
11 сынып Алгебра және анализ бастамалары пәнінен байқау емтихан тапсырмалары
А бөлімі
1) Теңдеуді шешіңіз: 2x2–5x–7=0. [1]
A) –0,5;
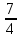 B) 1; –3,5 C) 0,5; –
B) 1; –3,5 C) 0,5; –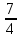 D) –1; 3,5 E) 3,5; 1
D) –1; 3,5 E) 3,5; 12) Нүкте түзу бойымен s = 2t3
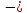 t2 + 5 заңы бойынша қозғалады. t =2 кезiндегi нүктенiң жылдамдығын
t2 + 5 заңы бойынша қозғалады. t =2 кезiндегi нүктенiң жылдамдығын табыңыз: [1]
А) 33 В) 20 С) 16 D) 17 Е) 28.
3) Өрнектің ең кіші мәні: 5 - 3 cos
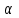 . [1]
. [1] A)8 B) -5 C)1 D) 2 E) 0
4) Анықталу облысын табыңыз: y =
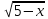 +log2х. [1]
+log2х. [1]А) (-∞ ; 0) В) (0; 2) С) (2; 5] D) ( 2; 5) Е) (0; 5]
5) Есептеңіз:
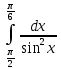 . [1]
. [1]A)
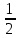 B) -
B) - 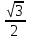 C)
C) 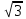 D) -
D) -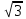 E)
E) 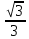
6) Өрнекті ықшамдаңыз:
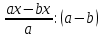 . [1]
. [1]А)
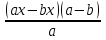 В)
В) 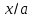 С)
С) 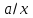 D)
D) 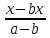 Е)
Е) 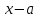
7) Теңдеуді шешіңіз:
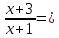
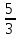 [1]
[1] А) 3 В) 2 С) 5 D) 4 Е) 3,5
8)
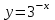 және
және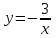 функцияларының қиылысу нүктелері: [1]
функцияларының қиылысу нүктелері: [1]A) (0;1) B) (1;3) C) (-1;3) D) (-1;0) E)(-1;-3)
9)Өрнекті көпмүше түріне келтіріңіз: (
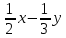 )(
)(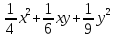
)[1]
А)
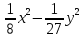 В)
В) 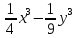 С)
С) 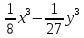 D)
D)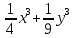 Е)
Е)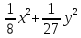
10) Функция мәндерінің жиынын табыңыз: у= х
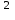 -6х+5. [1]
-6х+5. [1]А) у
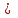 -2 В) у
-2 В) у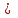 6 С) -6
6 С) -6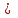 у
у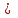 0 D) у
0 D) у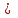 -4 Е) -3
-4 Е) -3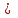 у
у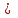 5
5| NN | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Жауабы | D | B | D | E | D | B | B | C | C | D |
B бөлімі
11) y = sіn(1-4x) функциясының периодын табыңыз.
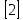
12) Теңдеуді шешіңіз:
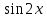
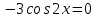 .
. 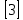
13) Егер log3х
 3log32+
3log32+ log325-2log34 болса, х-тің мәнін табыңыз.
log325-2log34 болса, х-тің мәнін табыңыз. 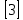
14) y=x4-2x2-8 функциясы үшін экстремум нүктелерiнiң ординаталарының қосындысын табыңыз.
15) Теңсіздіктер жүйесін шешіңіз:
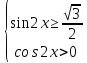

16) f(x)=4sin3xcos3х функциясы үшiн алғашқы функциясының жалпы түрiн табыңыз.

Балл қою схемасы
| Тапсырма | Жауап | Балл | Қосымша ақпарат |
| 11 | y = sіn (1- 4x) k  - 4, - 4, 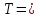 2 2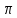 | 1 | синус функциясының периодын қолданады |
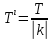 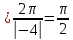 | 1 | | |
| 12 |   / / 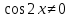 | 1 | Әдісі үшін балл қойылады |
| tg2х-3  0 02х  arctg arctg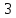 + +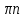 , , 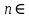 Z, Z, | 1 | Тангенс функциясының анықталу облысын ескереді | |
| х 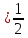 arctg arctg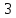 + +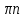 , , 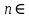 Z Z | 1 | Шешімін жазады | |
| 13 | log3х  3log32+ 3log32+ log325-2log34 log325-2log34 | | Логарифмнің қасиеттерін қолданады |
| 3log32  log38, log38,  log325 log325 log35, log35, 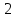 log34 log34 log316 log316 | 1 | ||
| log3х  log38+ log35- log316 log38+ log35- log316 log3 log3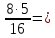 log3 log3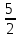 | 1 | Өрнекті түрлендіреді | |
| log3х  log3 log3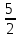 бұдан х бұдан х 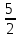 немесе х немесе х 2,5 2,5 | 1 | х-тің мәнін жазады | |
| 14 | 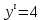 x3-4x x3-4x | 1 | Функция туындысын табады |
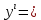 0, 4x(x2-1) 0, 4x(x2-1) 0 , 0 ,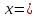 0, 0, 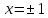 | 1 | Экстремум шартын қолданады | |
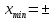 1, 1, 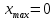 | 1 | Аралықтар әдісімен экстремум түрлерін анықтайды | |
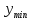 + +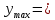 (1-2-8) (1-2-8)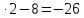 | 1 | | |
| 15 | 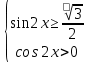 | 1 | |
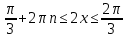 + +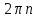 , n , n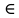 Z Z 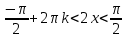 + +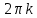 , k , k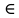 Z Z | 1 | Әр теңсіздіктің шешімін табады | |
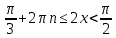 + +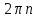 , n , n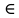 Z Z | 1 | Шешімдерінің қиылысуын табады | |
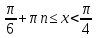 + +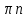 , n , n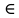 Z Z | 1 | Түрлендірулер жасайды | |
| | Баламалы әдіс те қабылданады | ||
| 16 | 2sin 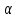 cos cos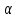 =sin2 =sin2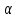 | 1 | Есепті шешу әдісі үшін балл қойылады |
| 4sin3x cos3х =2 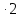 sin3x cos3х =2sin6x sin3x cos3х =2sin6x | 1 | Тригонометрияның қос аргумент формулаларын қолданады | |
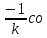 skх skх | 1 | Күрделі функцияның алғашқы функциясының формуласын қолданылады | |
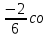 s6х +С= s6х +С=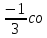 s6х +С s6х +С | 1 | алғашқы функциясының жалпы түрiн жазады | |
| Барлығы | 30 | | |