ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.12.2023
Просмотров: 23
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
Кафедра безопасности информационных систем
Лабораторная работа №10
на тему:
«Выполнение практических работ»
по дисциплине «Теория информации, данные, знания»
Вариант №7
Выполнил: студенты группы ИСТ-132
Шаталов Т. В.
Бабаева Д. О.
Принял: к.т.н., доцент Литвинов В.Л.
Задание:
Задача 1. Источник сообщений выдает символы из алфавита A = {ai}, i = 1, … ,4 с вероятностями (см. таблицу 1) p1, p2, p3, p4. Найти энтропию и избыточность источника сообщений.
Задача 2. Рассмотрим следующий процесс: мы замеряем некоторую величину ξ, которая является количеством фотонов, которые регистрируются фоточувствительной пластиной. Пусть источник света в единицу времени генерирует N фотонов. Каждый фотон с вероятностью p1 может рассеяться на частицах среды, находящейся между источником и пластиной и не достичь фоточувствительной пластины. С вероятностью p2 фотон, достигший фоточувствительной пластины, может быть зарегистрирован пластиной. Какое количество информации содержится в сообщении, что зарегистрировано M фотонов?
Задача 3. Первичный алфавит состоит из трех знаков с вероятностями p1, p2, p. При этом p1 и p2 заданы в табл.1 и p1+p2+p=1. Для передачи по каналу без помех используется равномерный двоичный код. Средняя длительность передачи одного элемента сообщения в канале
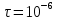с. Определить пропускную способность канала и скорость передачи информации. Можно ли приблизить скорость передачи к пропускной способности данной системы?Задача 4. Сколько информационных и проверочных символов содержится в двоичном коде, исправляющем ровно t ошибок при общем числе разрешенных кодовых комбинаций, равном N.
Ход работы:
Задача 1. Источник сообщений выдает символы из алфавита
A = {ai}, i = 1, … ,4 с вероятностями (см. таблицу 1) p1, p2, p3, p4. Найти энтропию и избыточность источника сообщений.
Вычислим энтропию источника по формуле Шеннона:
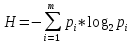
Исходя из исходных данных, p1 = 0.6, p2 = 0.1, p3 = 0.2, p4 = 0.1 получаем:
H = -(0.2 * log2(0.2) + 0.4 * log2(0.4) + 0.3 * log2(0.3) + 0.1* log2(0.1)) = 1.8465
Вычислим избыточность источника по следующей формуле:
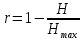
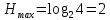
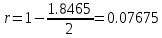
Задача 2. Рассмотрим следующий процесс: мы замеряем некоторую величину ξ, которая является количеством фотонов, которые регистрируются фоточувствительной пластиной. Пусть источник света в единицу времени генерирует N = 256 фотонов. Каждый фотон с вероятностью p1=0.2 может рассеяться на частицах среды, находящейся между источником и пластиной и не достичь фоточувствительной пластины. С вероятностью p2=0.4 фотон, достигший фоточувствительной пластины, может быть зарегистрирован пластиной. Какое количество информации содержится в сообщении, что зарегистрировано M=11 фотонов?
Вероятность того, что фотон достигнет фоточувствительной пластины равна
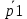= 0.8. Вероятность того, что достигший фотон будет еще и зафиксирован равен p = 
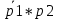= 0.32Для вычисления количества информации, содержащегося в сообщении о регистрации M = 11 фотонов, мы можем использовать формулу Шеннона:
I = -log2(p)
где p - вероятность наступления события.
В данном случае, вероятность того, что достигший фотон будет зарегистрирован, равна p = 0.32. Подставляя это значение в формулу, получаем:
I = -log2(0.32)
Выполняя вычисления, получаем:
I = -log2(2^(-2)) (так как 0.32 = 2^(-2))
I = -(-2) (по свойству логарифма log2(2^(-n)) = -n)
I = 2
Таким образом, количество информации, содержащейся в сообщении о регистрации 11 фотонов, составляет 2 бита.
Задача 3. Первичный алфавит состоит из трех знаков с вероятностями p1, p2, p. При этом p1 и p2 заданы в табл.1 и p1+p2+p=1. Для передачи по каналу без помех используется равномерный двоичный код. Средняя длительность передачи одного элемента сообщения в канале
с. Определить пропускную способность канала и скорость передачи информации. Можно ли приблизить скорость передачи к пропускной способности данной системы?Определим пропускную способность с помощью частоты передачи, так как сигнал двоичный (m = 2)
= 
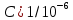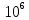бит/с.Из условия получаем, что p = 1 – p1 – p2 = 0.4, а энтропия источника:
H = – (0.2
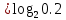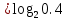+0.4
+0.4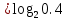 ) = 1.52 бит/с.Из следующей формулы находим скорость передачи информации:
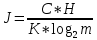
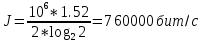
Если скорость передачи информации, которая была вычислена, оказывается меньше пропускной способности канала связи, то можно увеличить скорость передачи, приблизив длину кода к значению реальной энтропии источника.
Это означает, что можно использовать более эффективные кодировочные схемы, которые позволяют уплотнить информацию и использовать меньше битов для передачи той же самой информации. Приближение длины кода к реальной энтропии источника позволяет более эффективно использовать доступную пропускную способность канала связи и передавать больше информации за тот же промежуток времени.
Задача 4. Сколько информационных и проверочных символов содержится в двоичном коде, исправляющем ровно t = 2 ошибок при общем числе разрешенных кодовых комбинаций, равном N = 64.
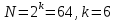
Число возможных однократных ошибок в коде длиной n равно n. Тогда справедливо выражение по Хеммингу:
r ≥
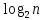и n = k + r n – k ≥
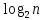
n ≥
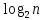
+ 6
n = 12, следовательно k = 8 и r = 4.
Таким образом, в каждой кодовой комбинации будет k = 8 информационных символов, и r = 4 проверочных.
Вывод
В данной лабораторной работе были получены практические навыки по основам теории информации. В результате были рассмотрены задачи расчёта энтропии и избыточности источника сообщения, определения количества информационных и проверочных символов и пропускной способности.
Санкт-Петербург
2021